Discovering Optimal Natural Gaits of Dissipative Systems via Virtual Energy Injection

Legged robots offer several advantages when navigating unstructured environments, but they often fall short of the efficiency achieved by wheeled robots. One promising strategy to improve their energy economy is to leverage their natural (unactuated) dynamics using elastic elements. This work explores that concept by designing energy-optimal control inputs through a unified, multi-stage framework. It starts with a novel energy injection technique to identify passive motion patterns by harnessing the system's natural dynamics. This enables the discovery of passive solutions even in systems with energy dissipation caused by factors such as friction or plastic collisions. Building on these passive solutions, we then employ a continuation approach to derive energy-optimal control inputs for the fully actuated, dissipative robotic system. The method is tested on simulated models to demonstrate its applicability in both single- and multi-legged robotic systems. This analysis provides valuable insights into the design and operation of elastic legged robots, offering pathways to improve their efficiency and adaptability by exploiting the natural system dynamics.

Swing-Up of a Weakly Actuated Double Pendulum via Nonlinear Normal Modes

We identify the nonlinear normal modes spawning from the stable equilibrium of a double pendulum under gravity, and we establish their connection to homoclinic orbits through the unstable upright position as energy increases. This result is exploited to devise an efficient swing-up strategy for a double pendulum with weak, saturating actuators. Our approach involves stabilizing the system onto periodic orbits associated with the nonlinear modes while gradually injecting energy. Since these modes are autonomous system evolutions, the required control effort for stabilization is minimal. Even with actuator limitations of less than 1% of the maximum gravitational torque, the proposed method accomplishes the swing-up of the double pendulum by allowing sufficient time.

Nonlinear Modes as a Tool for Comparing the Mathematical Structure of Dynamic Models of Soft Robots

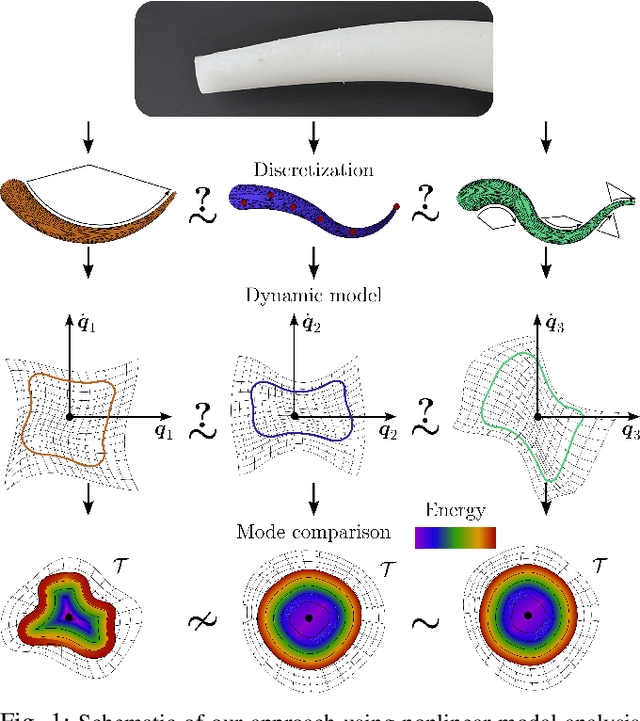
Continuum soft robots are nonlinear mechanical systems with theoretically infinite degrees of freedom (DoFs) that exhibit complex behaviors. Achieving motor intelligence under dynamic conditions necessitates the development of control-oriented reduced-order models (ROMs), which employ as few DoFs as possible while still accurately capturing the core characteristics of the theoretically infinite-dimensional dynamics. However, there is no quantitative way to measure if the ROM of a soft robot has succeeded in this task. In other fields, like structural dynamics or flexible link robotics, linear normal modes are routinely used to this end. Yet, this theory is not applicable to soft robots due to their nonlinearities. In this work, we propose to use the recent nonlinear extension in modal theory -- called eigenmanifolds -- as a means to evaluate control-oriented models for soft robots and compare them. To achieve this, we propose three similarity metrics relying on the projection of the nonlinear modes of the system into a task space of interest. We use this approach to compare quantitatively, for the first time, ROMs of increasing order generated under the piecewise constant curvature (PCC) hypothesis with a high-dimensional finite element (FE)-like model of a soft arm. Results show that by increasing the order of the discretization, the eigenmanifolds of the PCC model converge to those of the FE model.