Design and Control of a Recovery System for Legged Robots

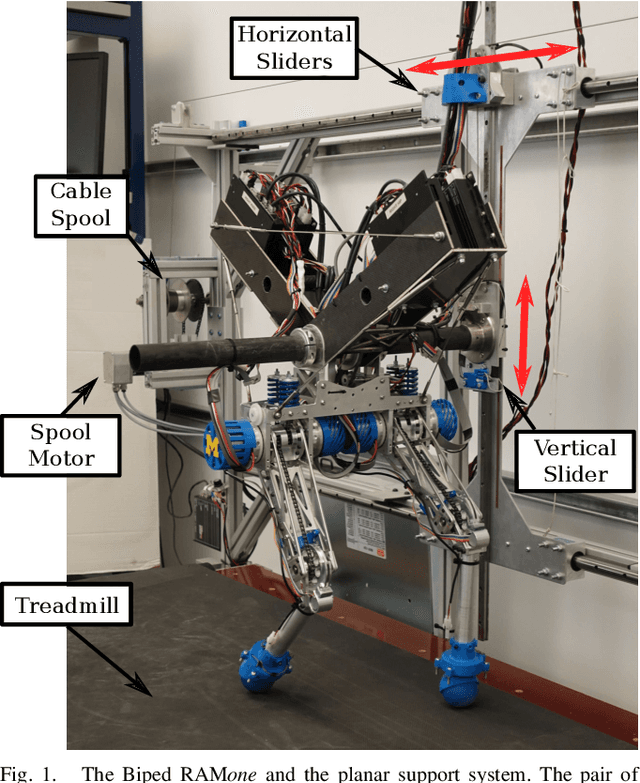
This paper describes the design and control of a support and recovery system for use with planar legged robots. The system operates in three modes. First, it can be operated in a fully transparent mode where no forces are applied to the robot. In this mode, the system follows the robot closely to be able to quickly catch the robot if needed. Second, it can provide a vertical supportive force to assist a robot during operation. Third, it can catch the robot and pull it away from the ground after a failure to avoid falls and the associated damages. In this mode, the system automatically resets the robot after a trial allowing for multiple consecutive trials to be run without manual intervention. The supportive forces are applied to the robot through an actuated cable and pulley system that uses series elastic actuation with a unidirectional spring to enable truly transparent operation. The nonlinear nature of this system necessitates careful design of controllers to ensure predictable, safe behaviors. In this paper we introduce the mechatronic design of the recovery system, develop suitable controllers, and evaluate the system's performance on the bipedal robot RAMone.

Walking with Confidence: Safety Regulation for Full Order Biped Models

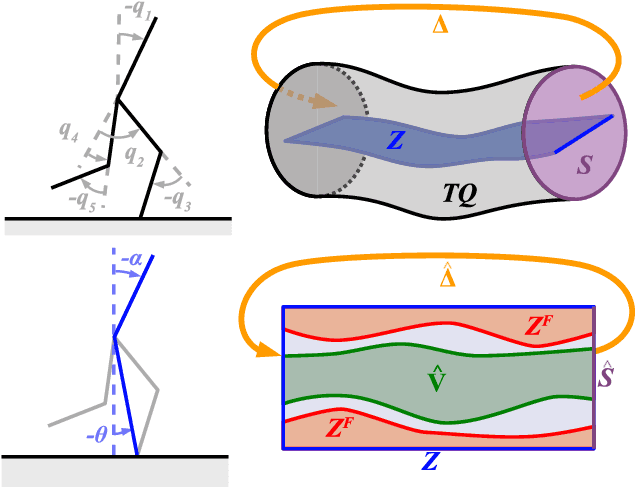
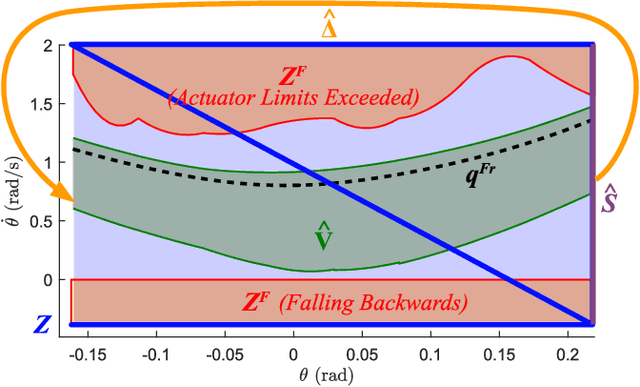
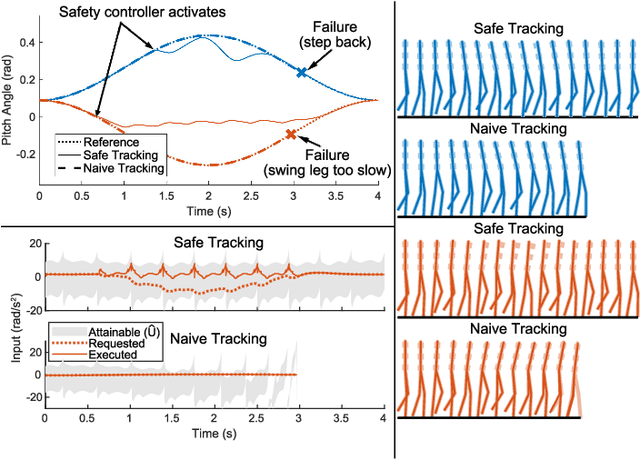
Safety guarantees are valuable in the control of walking robots, as falling can be both dangerous and costly. Unfortunately, set-based tools for generating safety guarantees (such as sums-of-squares optimization) are typically restricted to simplified, low-dimensional models of walking robots. For more complex models, methods based on hybrid zero dynamics can ensure the local stability of a pre-specified limit cycle, but provide limited guarantees. This paper combines the benefits of both approaches by using sums-of-squares optimization on a hybrid zero dynamics manifold to generate a guaranteed safe set for a 10-dimensional walking robot model. Along with this set, this paper describes how to generate a controller that maintains safety by modifying the manifold parameters when on the edge of the safe set. The proposed approach, which is applied to a bipedal Rabbit model, provides a roadmap for applying sums-of-squares verification techniques to high dimensional systems. This opens the door for a broad set of tools that can generate safety guarantees and regulating controllers for complex walking robot models.

Learning Stable and Energetically Economical Walking with RAMone

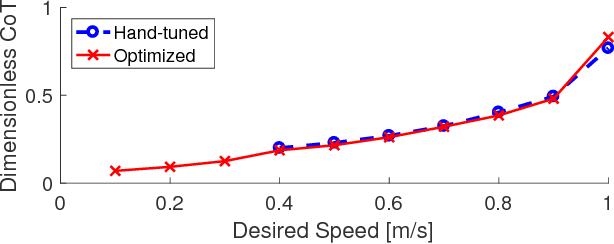
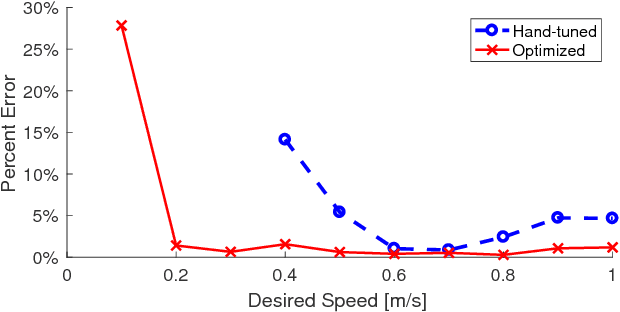
In this paper, we optimize over the control parameter space of our planar-bipedal robot, RAMone, for stable and energetically economical walking at various speeds. We formulate this task as an episodic reinforcement learning problem and use Covariance Matrix Adaptation. The parameters we are interested in modifying include gains from our Hybrid Zero Dynamics style controller and from RAMone's low-level motor controllers.