There is HOPE to Avoid HiPPOs for Long-memory State Space Models
Paper and Code
May 22, 2024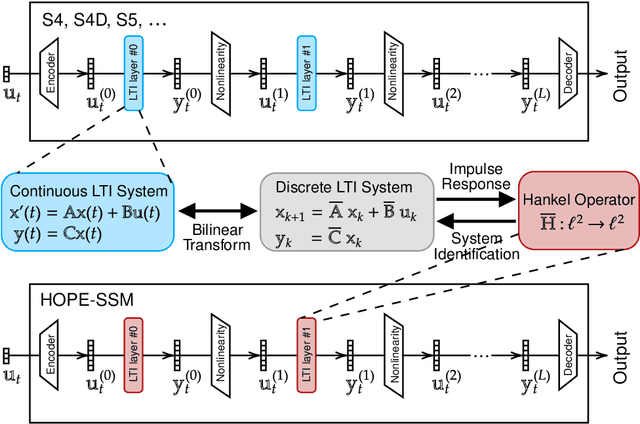
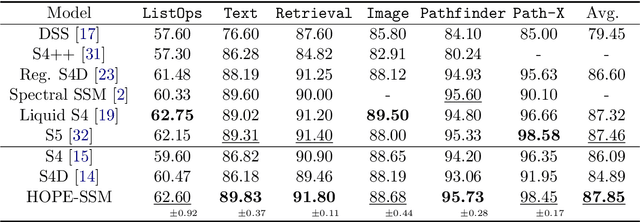
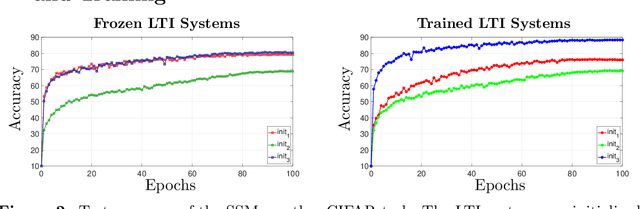
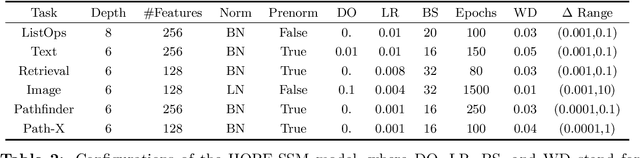
State-space models (SSMs) that utilize linear, time-invariant (LTI) systems are known for their effectiveness in learning long sequences. However, these models typically face several challenges: (i) they require specifically designed initializations of the system matrices to achieve state-of-the-art performance, (ii) they require training of state matrices on a logarithmic scale with very small learning rates to prevent instabilities, and (iii) they require the model to have exponentially decaying memory in order to ensure an asymptotically stable LTI system. To address these issues, we view SSMs through the lens of Hankel operator theory, which provides us with a unified theory for the initialization and training of SSMs. Building on this theory, we develop a new parameterization scheme, called HOPE, for LTI systems that utilizes Markov parameters within Hankel operators. This approach allows for random initializations of the LTI systems and helps to improve training stability, while also provides the SSMs with non-decaying memory capabilities. Our model efficiently implements these innovations by nonuniformly sampling the transfer functions of LTI systems, and it requires fewer parameters compared to canonical SSMs. When benchmarked against HiPPO-initialized models such as S4 and S4D, an SSM parameterized by Hankel operators demonstrates improved performance on Long-Range Arena (LRA) tasks. Moreover, we use a sequential CIFAR-10 task with padded noise to empirically corroborate our SSM's long memory capacity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge