Trimmed Constrained Mixed Effects Models: Formulations and Algorithms

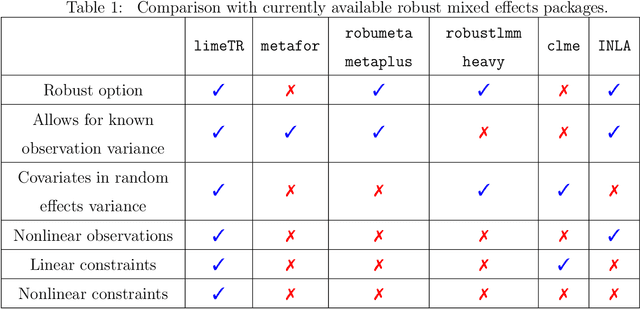
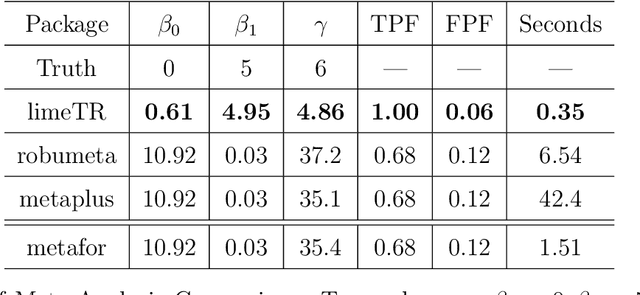
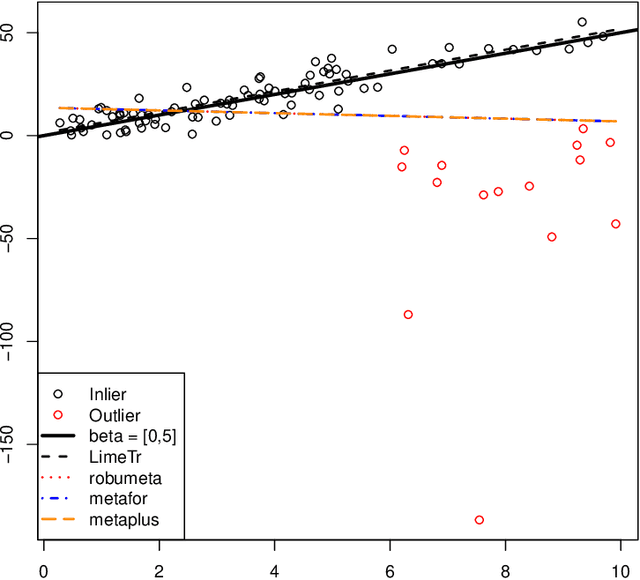
Mixed effects (ME) models inform a vast array of problems in the physical and social sciences, and are pervasive in meta-analysis. We consider ME models where the random effects component is linear. We then develop an efficient approach for a broad problem class that allows nonlinear measurements, priors, and constraints, and finds robust estimates in all of these cases using trimming in the associated marginal likelihood. We illustrate the efficacy of the approach on a range of applications for meta-analysis of global health data. Constraints and priors are used to impose monotonicity, convexity and other characteristics on dose-response relationships, while nonlinear observations enable new epidemiological analyses in place of approximations. Robust extensions ensure that spurious studies do not drive our understanding of between-study heterogeneity. The software accompanying this paper is disseminated as an open-source Python package called limeTR.