Simple and Nearly-Optimal Sampling for Rank-1 Tensor Completion via Gauss-Jordan

We revisit the sample and computational complexity of completing a rank-1 tensor in $\otimes_{i=1}^{N} \mathbb{R}^{d}$, given a uniformly sampled subset of its entries. We present a characterization of the problem (i.e. nonzero entries) which admits an algorithm amounting to Gauss-Jordan on a pair of random linear systems. For example, when $N = \Theta(1)$, we prove it uses no more than $m = O(d^2 \log d)$ samples and runs in $O(md^2)$ time. Moreover, we show any algorithm requires $\Omega(d\log d)$ samples. By contrast, existing upper bounds on the sample complexity are at least as large as $d^{1.5} \mu^{\Omega(1)} \log^{\Omega(1)} d$, where $\mu$ can be $\Theta(d)$ in the worst case. Prior work obtained these looser guarantees in higher rank versions of our problem, and tend to involve more complicated algorithms.

Single-Server Private Information Retrieval with Side Information Under Arbitrary Popularity Profiles

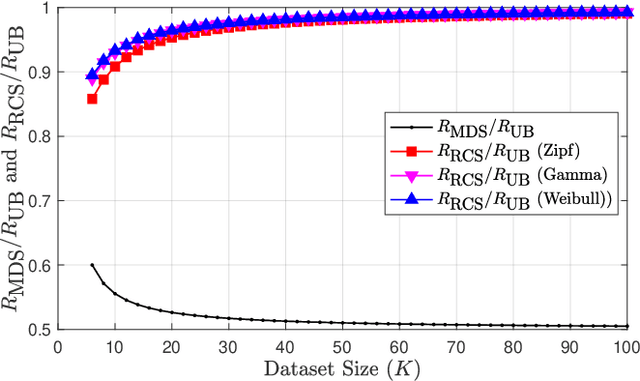
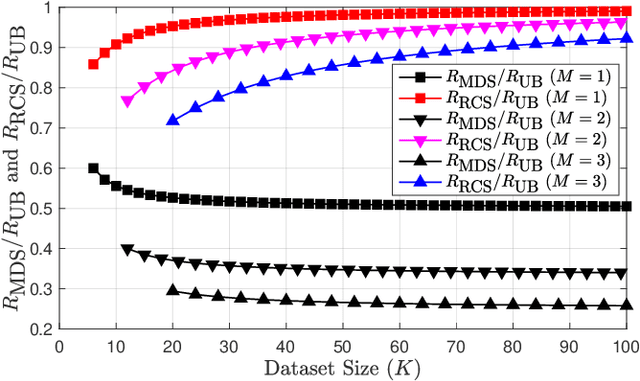
This paper introduces a generalization of the Private Information Retrieval with Side Information (PIR-SI) problem called Popularity-Aware PIR-SI (PA-PIR-SI). The PA-PIR-SI problem includes one or more remote servers storing copies of a dataset of $K$ messages, and a user who knows $M$ out of $K$ messages -- the identities of which are unknown to the server -- as a prior side information, and wishes to retrieve one of the remaining $K-M$ messages. The goal of the user is to minimize the amount of information they must download from the server while revealing no information about the identity of the desired message. In contrast to PIR-SI, in PA-PIR-SI, the dataset messages are not assumed to be equally popular. That is, given the $M$ side information messages, each of the remaining $K-M$ messages is not necessarily equally likely to be the message desired by the user. In this work, we focus on the single-server setting of PA-PIR-SI, and establish lower and upper bounds on the capacity of this setting -- defined as the maximum possible achievable download rate. Our upper bound holds for any message popularity profile, and is the same as the capacity of single-server PIR-SI. We prove the lower bound by presenting a PA-PIR-SI scheme which takes a novel probabilistic approach -- carefully designed based on the popularity profile -- to integrate two existing PIR-SI schemes. The rate of our scheme is strictly higher than that of the only existing PIR-SI scheme applicable to the PA-PIR-SI setting.