A Latent-Variable Formulation of the Poisson Canonical Polyadic Tensor Model: Maximum Likelihood Estimation and Fisher Information

We establish parameter inference for the Poisson canonical polyadic (PCP) tensor model through a latent-variable formulation. Our approach exploits the observation that any random PCP tensor can be derived by marginalizing an unobservable random tensor of one dimension larger. The loglikelihood of this larger dimensional tensor, referred to as the "complete" loglikelihood, is comprised of multiple rank one PCP loglikelihoods. Using this methodology, we first derive non-iterative maximum likelihood estimators for the PCP model and demonstrate that several existing algorithms for fitting non-negative matrix and tensor factorizations are Expectation-Maximization algorithms. Next, we derive the observed and expected Fisher information matrices for the PCP model. The Fisher information provides us crucial insights into the well-posedness of the tensor model, such as the role that tensor rank plays in identifiability and indeterminacy. For the special case of rank one PCP models, we demonstrate that these results are greatly simplified.

Near-Efficient and Non-Asymptotic Multiway Inference

We establish non-asymptotic efficiency guarantees for tensor decomposition-based inference in count data models. Under a Poisson framework, we consider two related goals: (i) parametric inference, the estimation of the full distributional parameter tensor, and (ii) multiway analysis, the recovery of its canonical polyadic (CP) decomposition factors. Our main result shows that in the rank-one setting, a rank-constrained maximum-likelihood estimator achieves multiway analysis with variance matching the Cram\'{e}r-Rao Lower Bound (CRLB) up to absolute constants and logarithmic factors. This provides a general framework for studying "near-efficient" multiway estimators in finite-sample settings. For higher ranks, we illustrate that our multiway estimator may not attain the CRLB; nevertheless, CP-based parametric inference remains nearly minimax optimal, with error bounds that improve on prior work by offering more favorable dependence on the CP rank. Numerical experiments corroborate near-efficiency in the rank-one case and highlight the efficiency gap in higher-rank scenarios.

Zero-Truncated Poisson Regression for Zero-Inflated Multiway Count Data

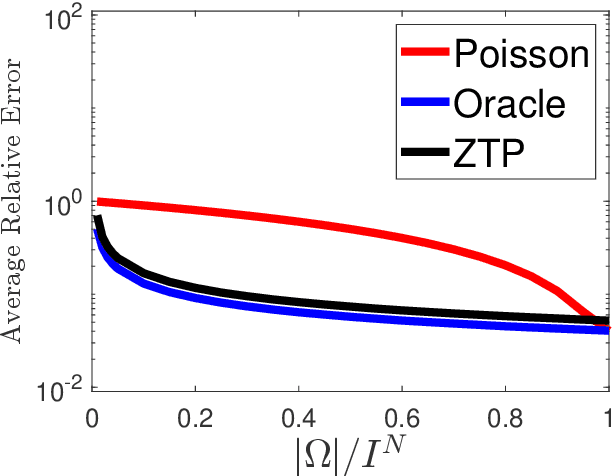
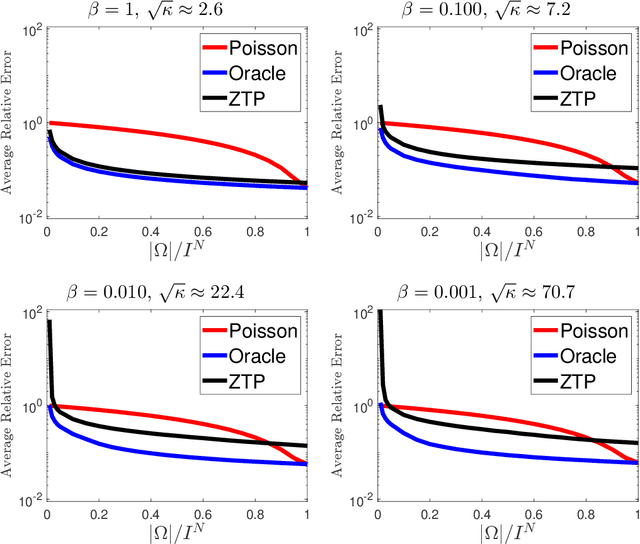
We propose a novel statistical inference paradigm for zero-inflated multiway count data that dispenses with the need to distinguish between true and false zero counts. Our approach ignores all zero entries and applies zero-truncated Poisson regression on the positive counts. Inference is accomplished via tensor completion that imposes low-rank structure on the Poisson parameter space. Our main result shows that an $N$-way rank-$R$ parametric tensor $\boldsymbol{\mathscr{M}}\in(0,\infty)^{I\times \cdots\times I}$ generating Poisson observations can be accurately estimated from approximately $IR^2\log_2^2(I)$ non-zero counts for a nonnegative canonical polyadic decomposition. Several numerical experiments are presented demonstrating that our zero-truncated paradigm is comparable to the ideal scenario where the locations of false zero counts are known a priori.

Using Neural Architecture Search for Improving Software Flaw Detection in Multimodal Deep Learning Models

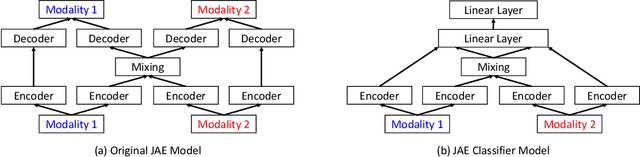
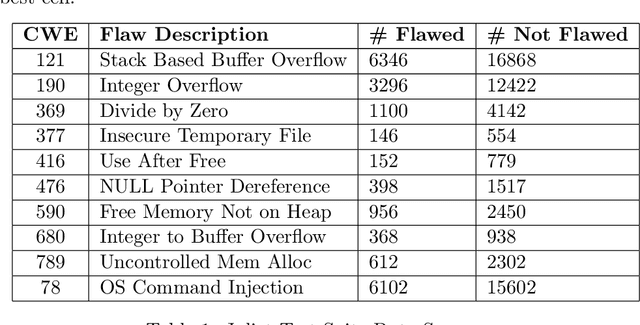
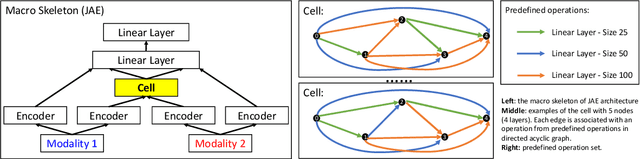
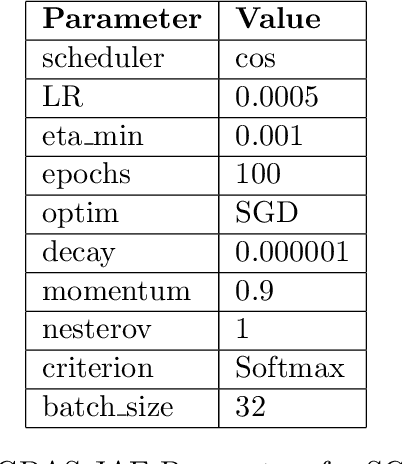
Software flaw detection using multimodal deep learning models has been demonstrated as a very competitive approach on benchmark problems. In this work, we demonstrate that even better performance can be achieved using neural architecture search (NAS) combined with multimodal learning models. We adapt a NAS framework aimed at investigating image classification to the problem of software flaw detection and demonstrate improved results on the Juliet Test Suite, a popular benchmarking data set for measuring performance of machine learning models in this problem domain.

Multimodal Deep Learning for Flaw Detection in Software Programs

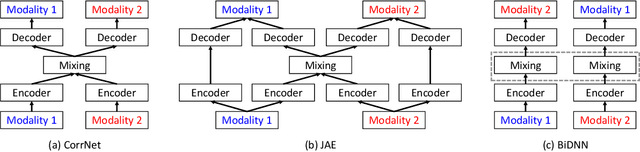
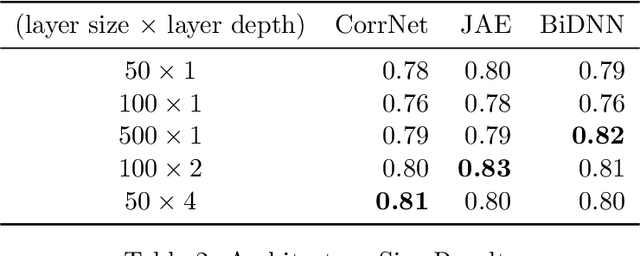
We explore the use of multiple deep learning models for detecting flaws in software programs. Current, standard approaches for flaw detection rely on a single representation of a software program (e.g., source code or a program binary). We illustrate that, by using techniques from multimodal deep learning, we can simultaneously leverage multiple representations of software programs to improve flaw detection over single representation analyses. Specifically, we adapt three deep learning models from the multimodal learning literature for use in flaw detection and demonstrate how these models outperform traditional deep learning models. We present results on detecting software flaws using the Juliet Test Suite and Linux Kernel.

All-at-once Optimization for Coupled Matrix and Tensor Factorizations

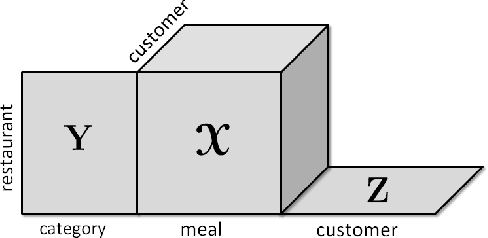
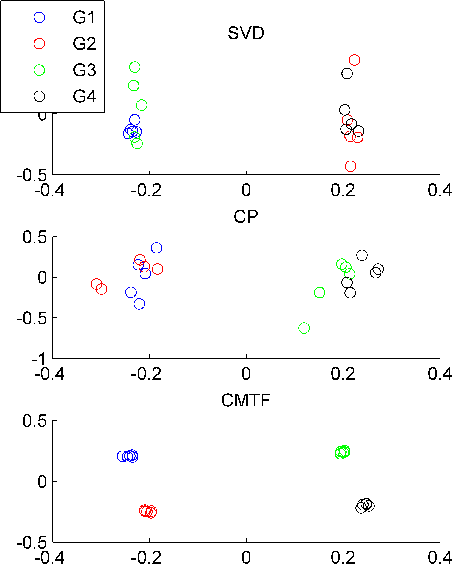
Joint analysis of data from multiple sources has the potential to improve our understanding of the underlying structures in complex data sets. For instance, in restaurant recommendation systems, recommendations can be based on rating histories of customers. In addition to rating histories, customers' social networks (e.g., Facebook friendships) and restaurant categories information (e.g., Thai or Italian) can also be used to make better recommendations. The task of fusing data, however, is challenging since data sets can be incomplete and heterogeneous, i.e., data consist of both matrices, e.g., the person by person social network matrix or the restaurant by category matrix, and higher-order tensors, e.g., the "ratings" tensor of the form restaurant by meal by person. In this paper, we are particularly interested in fusing data sets with the goal of capturing their underlying latent structures. We formulate this problem as a coupled matrix and tensor factorization (CMTF) problem where heterogeneous data sets are modeled by fitting outer-product models to higher-order tensors and matrices in a coupled manner. Unlike traditional approaches solving this problem using alternating algorithms, we propose an all-at-once optimization approach called CMTF-OPT (CMTF-OPTimization), which is a gradient-based optimization approach for joint analysis of matrices and higher-order tensors. We also extend the algorithm to handle coupled incomplete data sets. Using numerical experiments, we demonstrate that the proposed all-at-once approach is more accurate than the alternating least squares approach.

Temporal Link Prediction using Matrix and Tensor Factorizations

The data in many disciplines such as social networks, web analysis, etc. is link-based, and the link structure can be exploited for many different data mining tasks. In this paper, we consider the problem of temporal link prediction: Given link data for times 1 through T, can we predict the links at time T+1? If our data has underlying periodic structure, can we predict out even further in time, i.e., links at time T+2, T+3, etc.? In this paper, we consider bipartite graphs that evolve over time and consider matrix- and tensor-based methods for predicting future links. We present a weight-based method for collapsing multi-year data into a single matrix. We show how the well-known Katz method for link prediction can be extended to bipartite graphs and, moreover, approximated in a scalable way using a truncated singular value decomposition. Using a CANDECOMP/PARAFAC tensor decomposition of the data, we illustrate the usefulness of exploiting the natural three-dimensional structure of temporal link data. Through several numerical experiments, we demonstrate that both matrix- and tensor-based techniques are effective for temporal link prediction despite the inherent difficulty of the problem. Additionally, we show that tensor-based techniques are particularly effective for temporal data with varying periodic patterns.