Zero-Truncated Poisson Regression for Zero-Inflated Multiway Count Data
Paper and Code
Jan 25, 2022

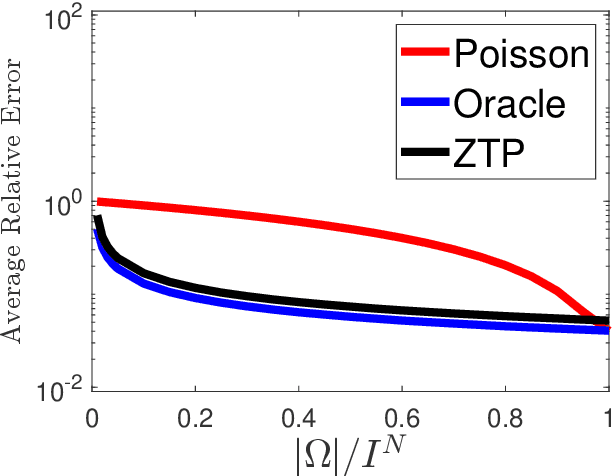
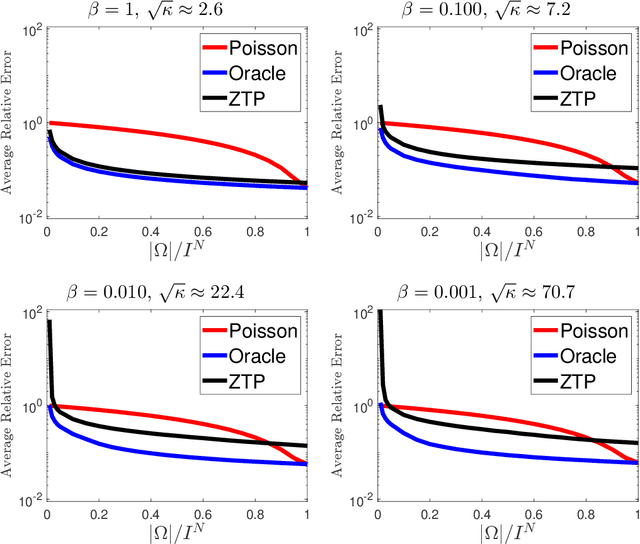
We propose a novel statistical inference paradigm for zero-inflated multiway count data that dispenses with the need to distinguish between true and false zero counts. Our approach ignores all zero entries and applies zero-truncated Poisson regression on the positive counts. Inference is accomplished via tensor completion that imposes low-rank structure on the Poisson parameter space. Our main result shows that an $N$-way rank-$R$ parametric tensor $\boldsymbol{\mathscr{M}}\in(0,\infty)^{I\times \cdots\times I}$ generating Poisson observations can be accurately estimated from approximately $IR^2\log_2^2(I)$ non-zero counts for a nonnegative canonical polyadic decomposition. Several numerical experiments are presented demonstrating that our zero-truncated paradigm is comparable to the ideal scenario where the locations of false zero counts are known a priori.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge