Near-Efficient and Non-Asymptotic Multiway Inference

We establish non-asymptotic efficiency guarantees for tensor decomposition-based inference in count data models. Under a Poisson framework, we consider two related goals: (i) parametric inference, the estimation of the full distributional parameter tensor, and (ii) multiway analysis, the recovery of its canonical polyadic (CP) decomposition factors. Our main result shows that in the rank-one setting, a rank-constrained maximum-likelihood estimator achieves multiway analysis with variance matching the Cram\'{e}r-Rao Lower Bound (CRLB) up to absolute constants and logarithmic factors. This provides a general framework for studying "near-efficient" multiway estimators in finite-sample settings. For higher ranks, we illustrate that our multiway estimator may not attain the CRLB; nevertheless, CP-based parametric inference remains nearly minimax optimal, with error bounds that improve on prior work by offering more favorable dependence on the CP rank. Numerical experiments corroborate near-efficiency in the rank-one case and highlight the efficiency gap in higher-rank scenarios.

A Latent-Variable Formulation of the Poisson Canonical Polyadic Tensor Model: Maximum Likelihood Estimation and Fisher Information

We establish parameter inference for the Poisson canonical polyadic (PCP) tensor model through a latent-variable formulation. Our approach exploits the observation that any random PCP tensor can be derived by marginalizing an unobservable random tensor of one dimension larger. The loglikelihood of this larger dimensional tensor, referred to as the "complete" loglikelihood, is comprised of multiple rank one PCP loglikelihoods. Using this methodology, we first derive non-iterative maximum likelihood estimators for the PCP model and demonstrate that several existing algorithms for fitting non-negative matrix and tensor factorizations are Expectation-Maximization algorithms. Next, we derive the observed and expected Fisher information matrices for the PCP model. The Fisher information provides us crucial insights into the well-posedness of the tensor model, such as the role that tensor rank plays in identifiability and indeterminacy. For the special case of rank one PCP models, we demonstrate that these results are greatly simplified.

Zero-Truncated Poisson Regression for Zero-Inflated Multiway Count Data

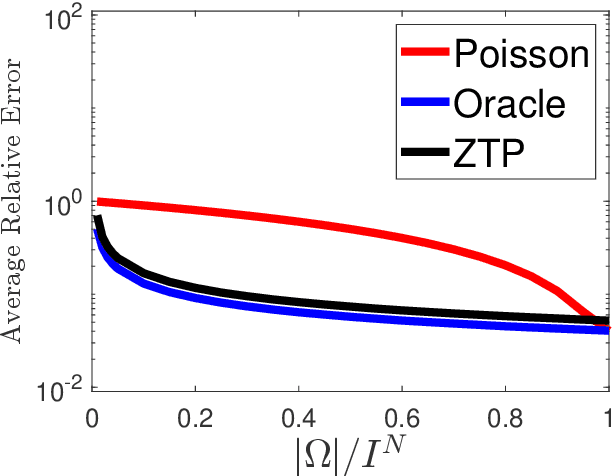
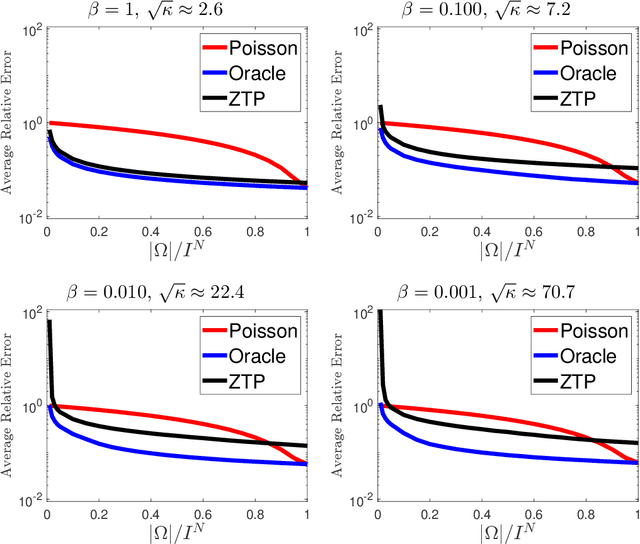
We propose a novel statistical inference paradigm for zero-inflated multiway count data that dispenses with the need to distinguish between true and false zero counts. Our approach ignores all zero entries and applies zero-truncated Poisson regression on the positive counts. Inference is accomplished via tensor completion that imposes low-rank structure on the Poisson parameter space. Our main result shows that an $N$-way rank-$R$ parametric tensor $\boldsymbol{\mathscr{M}}\in(0,\infty)^{I\times \cdots\times I}$ generating Poisson observations can be accurately estimated from approximately $IR^2\log_2^2(I)$ non-zero counts for a nonnegative canonical polyadic decomposition. Several numerical experiments are presented demonstrating that our zero-truncated paradigm is comparable to the ideal scenario where the locations of false zero counts are known a priori.

Neuromorphic scaling advantages for energy-efficient random walk computation

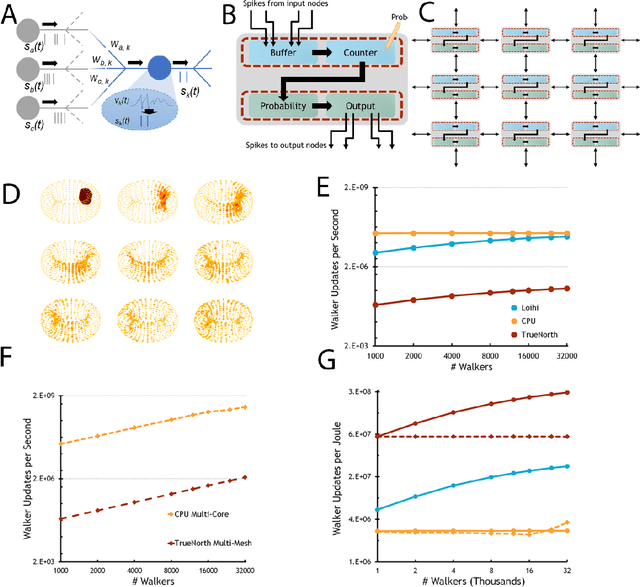
Computing stands to be radically improved by neuromorphic computing (NMC) approaches inspired by the brain's incredible efficiency and capabilities. Most NMC research, which aims to replicate the brain's computational structure and architecture in man-made hardware, has focused on artificial intelligence; however, less explored is whether this brain-inspired hardware can provide value beyond cognitive tasks. We demonstrate that high-degree parallelism and configurability of spiking neuromorphic architectures makes them well-suited to implement random walks via discrete time Markov chains. Such random walks are useful in Monte Carlo methods, which represent a fundamental computational tool for solving a wide range of numerical computing tasks. Additionally, we show how the mathematical basis for a probabilistic solution involving a class of stochastic differential equations can leverage those simulations to provide solutions for a range of broadly applicable computational tasks. Despite being in an early development stage, we find that NMC platforms, at a sufficient scale, can drastically reduce the energy demands of high-performance computing (HPC) platforms.

Solving a steady-state PDE using spiking networks and neuromorphic hardware

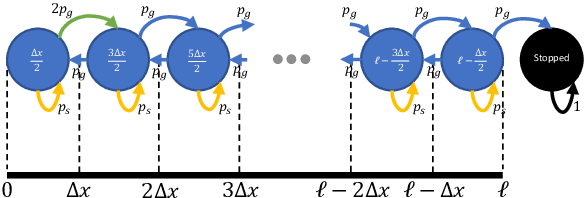
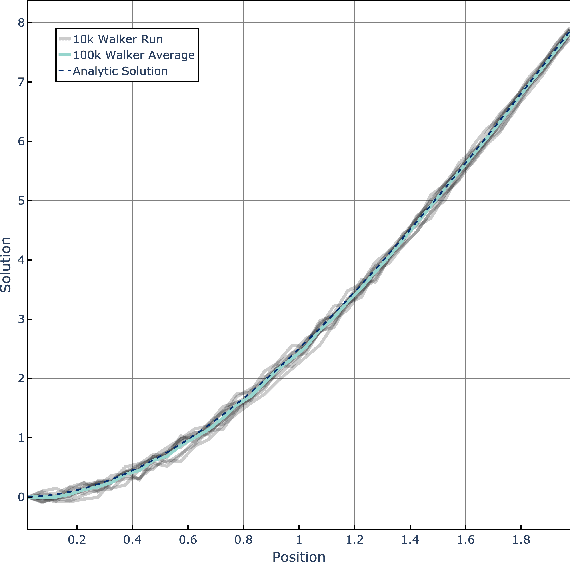
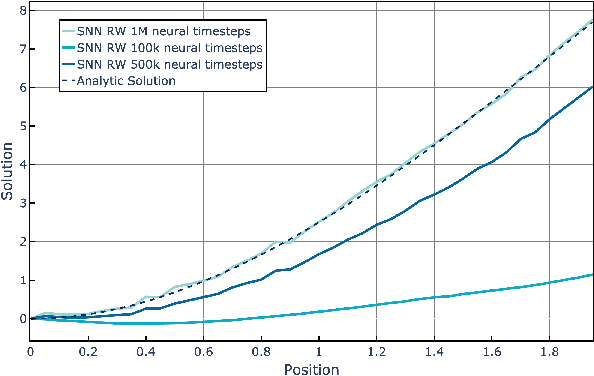
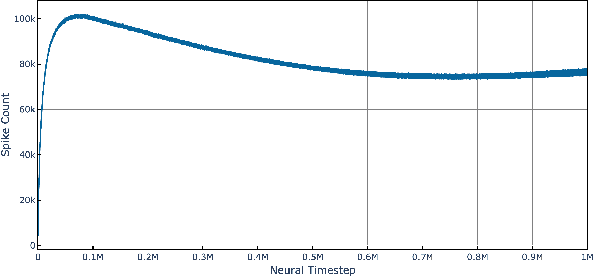
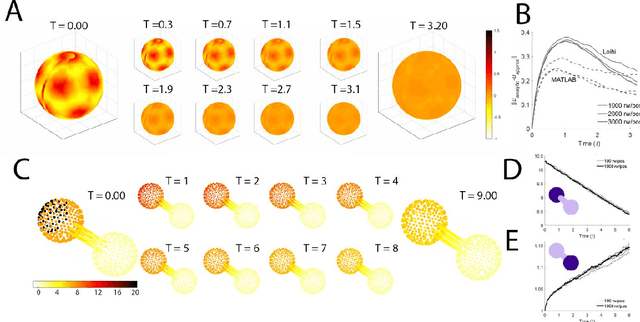
The widely parallel, spiking neural networks of neuromorphic processors can enable computationally powerful formulations. While recent interest has focused on primarily machine learning tasks, the space of appropriate applications is wide and continually expanding. Here, we leverage the parallel and event-driven structure to solve a steady state heat equation using a random walk method. The random walk can be executed fully within a spiking neural network using stochastic neuron behavior, and we provide results from both IBM TrueNorth and Intel Loihi implementations. Additionally, we position this algorithm as a potential scalable benchmark for neuromorphic systems.