Solving Sparse Finite Element Problems on Neuromorphic Hardware

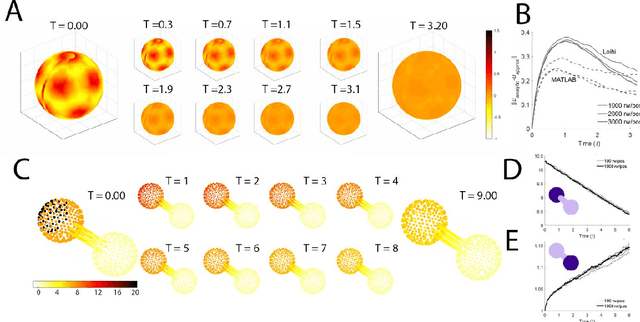
We demonstrate that scalable neuromorphic hardware can implement the finite element method, which is a critical numerical method for engineering and scientific discovery. Our approach maps the sparse interactions between neighboring finite elements to small populations of neurons that dynamically update according to the governing physics of a desired problem description. We show that for the Poisson equation, which describes many physical systems such as gravitational and electrostatic fields, this cortical-inspired neural circuit can achieve comparable levels of numerical accuracy and scaling while enabling the use of inherently parallel and energy-efficient neuromorphic hardware. We demonstrate that this approach can be used on the Intel Loihi 2 platform and illustrate how this approach can be extended to nontrivial mesh geometries and dynamics.

AI-Guided Codesign Framework for Novel Material and Device Design applied to MTJ-based True Random Number Generators

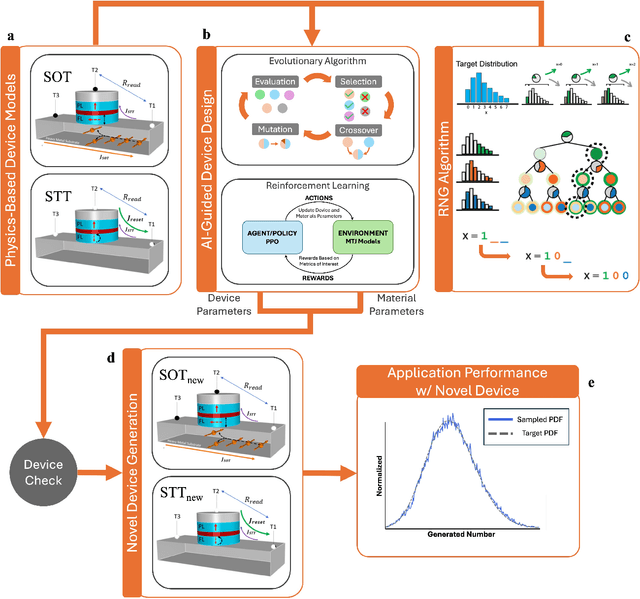
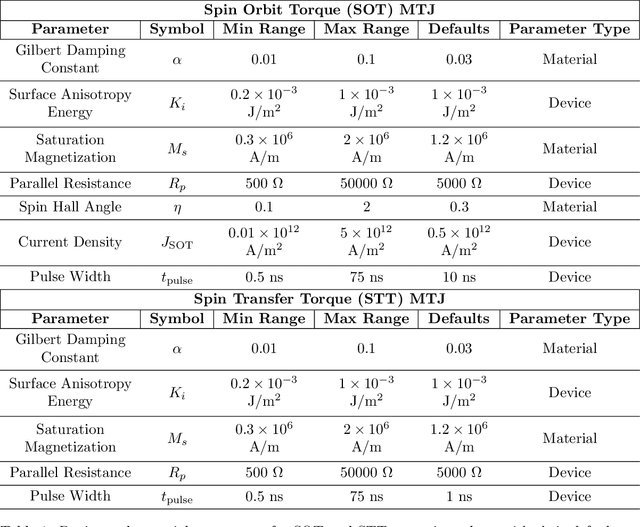
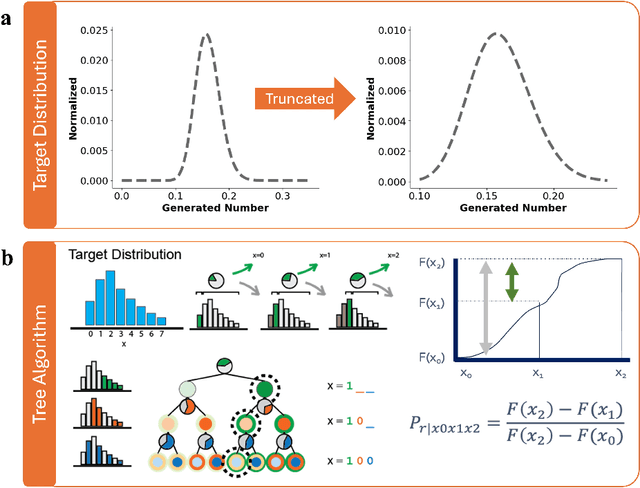
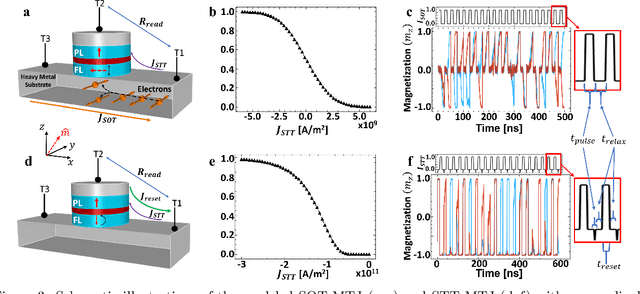
Novel devices and novel computing paradigms are key for energy efficient, performant future computing systems. However, designing devices for new applications is often time consuming and tedious. Here, we investigate the design and optimization of spin orbit torque and spin transfer torque magnetic tunnel junction models as the probabilistic devices for true random number generation. We leverage reinforcement learning and evolutionary optimization to vary key device and material properties of the various device models for stochastic operation. Our AI guided codesign methods generated different candidate devices capable of generating stochastic samples for a desired probability distribution, while also minimizing energy usage for the devices.

Neuromorphic Co-Design as a Game

Co-design is a prominent topic presently in computing, speaking to the mutual benefit of coordinating design choices of several layers in the technology stack. For example, this may be designing algorithms which can most efficiently take advantage of the acceleration properties of a given architecture, while simultaneously designing the hardware to support the structural needs of a class of computation. The implications of these design decisions are influential enough to be deemed a lottery, enabling an idea to win out over others irrespective of the individual merits. Coordination is a well studied topic in the mathematics of game theory, where in many cases without a coordination mechanism the outcome is sub-optimal. Here we consider what insights game theoretic analysis can offer for computer architecture co-design. In particular, we consider the interplay between algorithm and architecture advances in the field of neuromorphic computing. Analyzing developments of spiking neural network algorithms and neuromorphic hardware as a co-design game we use the Stag Hunt model to illustrate challenges for spiking algorithms or architectures to advance the field independently and advocate for a strategic pursuit to advance neuromorphic computing.

Synaptic Sampling of Neural Networks

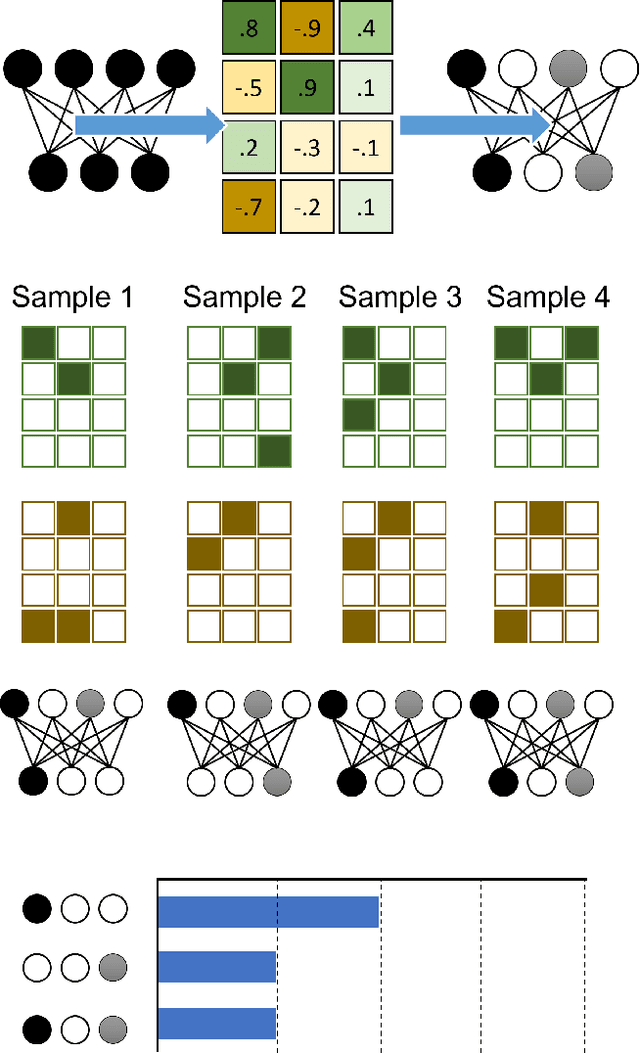
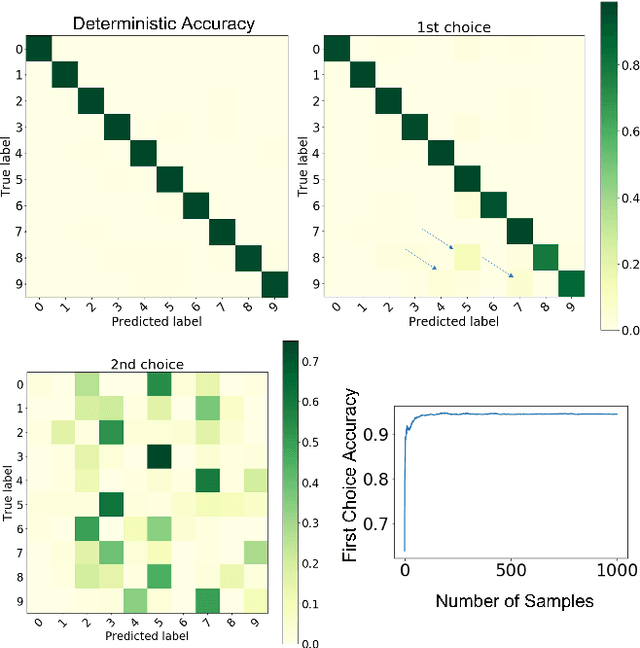
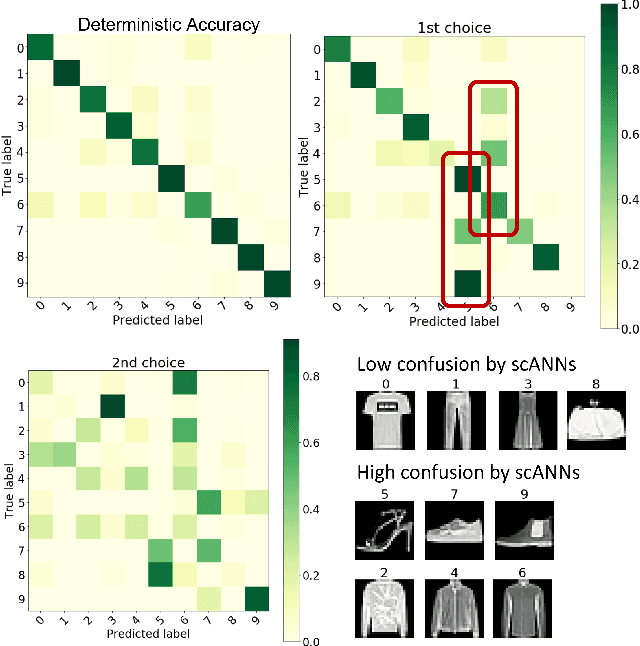
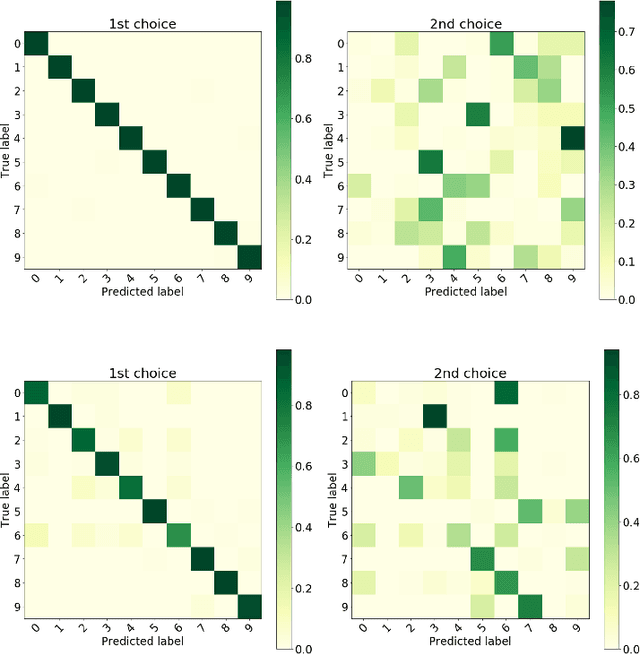
Probabilistic artificial neural networks offer intriguing prospects for enabling the uncertainty of artificial intelligence methods to be described explicitly in their function; however, the development of techniques that quantify uncertainty by well-understood methods such as Monte Carlo sampling has been limited by the high costs of stochastic sampling on deterministic computing hardware. Emerging computing systems that are amenable to hardware-level probabilistic computing, such as those that leverage stochastic devices, may make probabilistic neural networks more feasible in the not-too-distant future. This paper describes the scANN technique -- \textit{sampling (by coinflips) artificial neural networks} -- which enables neural networks to be sampled directly by treating the weights as Bernoulli coin flips. This method is natively well suited for probabilistic computing techniques that focus on tunable stochastic devices, nearly matches fully deterministic performance while also describing the uncertainty of correct and incorrect neural network outputs.

Design Principles for Lifelong Learning AI Accelerators

Lifelong learning - an agent's ability to learn throughout its lifetime - is a hallmark of biological learning systems and a central challenge for artificial intelligence (AI). The development of lifelong learning algorithms could lead to a range of novel AI applications, but this will also require the development of appropriate hardware accelerators, particularly if the models are to be deployed on edge platforms, which have strict size, weight, and power constraints. Here, we explore the design of lifelong learning AI accelerators that are intended for deployment in untethered environments. We identify key desirable capabilities for lifelong learning accelerators and highlight metrics to evaluate such accelerators. We then discuss current edge AI accelerators and explore the future design of lifelong learning accelerators, considering the role that different emerging technologies could play.

Decomposing spiking neural networks with Graphical Neural Activity Threads

A satisfactory understanding of information processing in spiking neural networks requires appropriate computational abstractions of neural activity. Traditionally, the neural population state vector has been the most common abstraction applied to spiking neural networks, but this requires artificially partitioning time into bins that are not obviously relevant to the network itself. We introduce a distinct set of techniques for analyzing spiking neural networks that decomposes neural activity into multiple, disjoint, parallel threads of activity. We construct these threads by estimating the degree of causal relatedness between pairs of spikes, then use these estimates to construct a directed acyclic graph that traces how the network activity evolves through individual spikes. We find that this graph of spiking activity naturally decomposes into disjoint connected components that overlap in space and time, which we call Graphical Neural Activity Threads (GNATs). We provide an efficient algorithm for finding analogous threads that reoccur in large spiking datasets, revealing that seemingly distinct spike trains are composed of similar underlying threads of activity, a hallmark of compositionality. The picture of spiking neural networks provided by our GNAT analysis points to new abstractions for spiking neural computation that are naturally adapted to the spatiotemporally distributed dynamics of spiking neural networks.

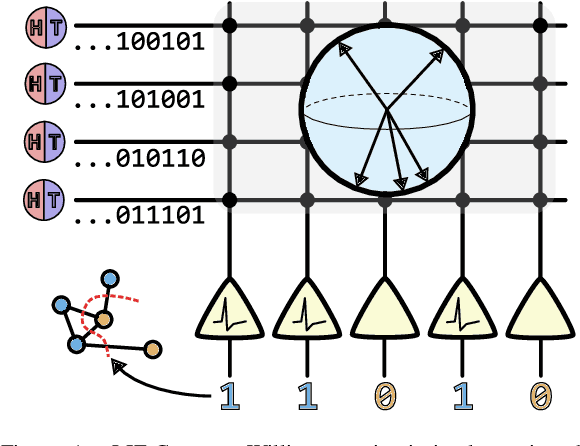
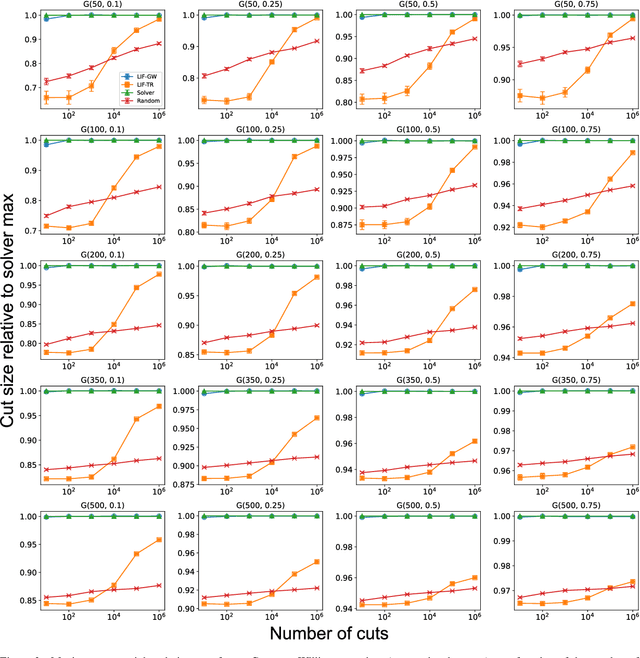
Stochastic Neuromorphic Circuits for Solving MAXCUT

Finding the maximum cut of a graph (MAXCUT) is a classic optimization problem that has motivated parallel algorithm development. While approximate algorithms to MAXCUT offer attractive theoretical guarantees and demonstrate compelling empirical performance, such approximation approaches can shift the dominant computational cost to the stochastic sampling operations. Neuromorphic computing, which uses the organizing principles of the nervous system to inspire new parallel computing architectures, offers a possible solution. One ubiquitous feature of natural brains is stochasticity: the individual elements of biological neural networks possess an intrinsic randomness that serves as a resource enabling their unique computational capacities. By designing circuits and algorithms that make use of randomness similarly to natural brains, we hypothesize that the intrinsic randomness in microelectronics devices could be turned into a valuable component of a neuromorphic architecture enabling more efficient computations. Here, we present neuromorphic circuits that transform the stochastic behavior of a pool of random devices into useful correlations that drive stochastic solutions to MAXCUT. We show that these circuits perform favorably in comparison to software solvers and argue that this neuromorphic hardware implementation provides a path for scaling advantages. This work demonstrates the utility of combining neuromorphic principles with intrinsic randomness as a computational resource for new computational architectures.

Spiking Neural Streaming Binary Arithmetic

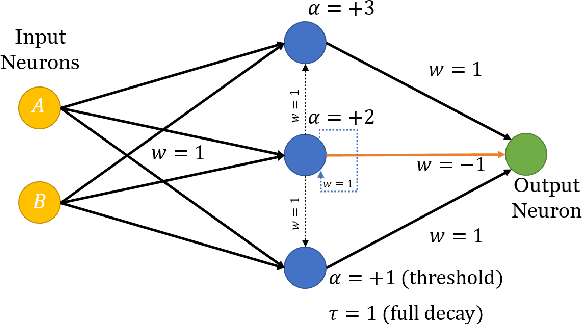
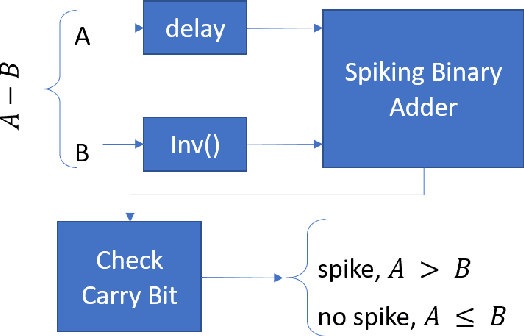
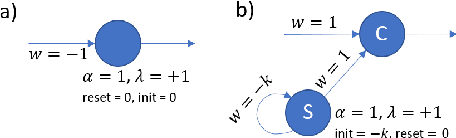
Boolean functions and binary arithmetic operations are central to standard computing paradigms. Accordingly, many advances in computing have focused upon how to make these operations more efficient as well as exploring what they can compute. To best leverage the advantages of novel computing paradigms it is important to consider what unique computing approaches they offer. However, for any special-purpose co-processor, Boolean functions and binary arithmetic operations are useful for, among other things, avoiding unnecessary I/O on-and-off the co-processor by pre- and post-processing data on-device. This is especially true for spiking neuromorphic architectures where these basic operations are not fundamental low-level operations. Instead, these functions require specific implementation. Here we discuss the implications of an advantageous streaming binary encoding method as well as a handful of circuits designed to exactly compute elementary Boolean and binary operations.

Neuromorphic scaling advantages for energy-efficient random walk computation

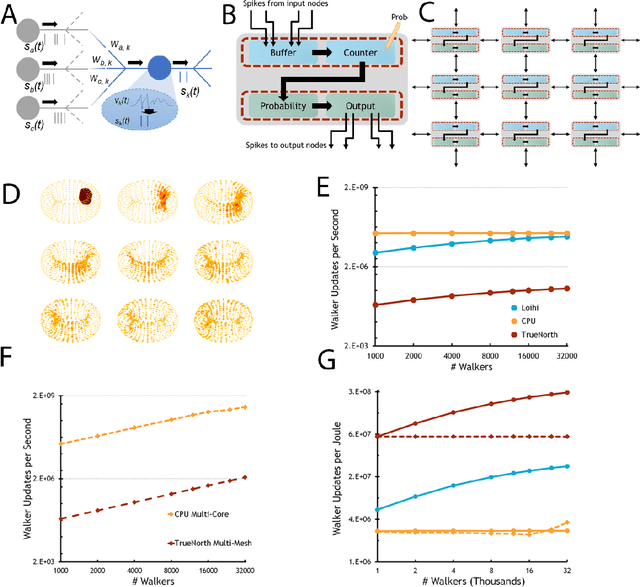
Computing stands to be radically improved by neuromorphic computing (NMC) approaches inspired by the brain's incredible efficiency and capabilities. Most NMC research, which aims to replicate the brain's computational structure and architecture in man-made hardware, has focused on artificial intelligence; however, less explored is whether this brain-inspired hardware can provide value beyond cognitive tasks. We demonstrate that high-degree parallelism and configurability of spiking neuromorphic architectures makes them well-suited to implement random walks via discrete time Markov chains. Such random walks are useful in Monte Carlo methods, which represent a fundamental computational tool for solving a wide range of numerical computing tasks. Additionally, we show how the mathematical basis for a probabilistic solution involving a class of stochastic differential equations can leverage those simulations to provide solutions for a range of broadly applicable computational tasks. Despite being in an early development stage, we find that NMC platforms, at a sufficient scale, can drastically reduce the energy demands of high-performance computing (HPC) platforms.

Constant-Depth and Subcubic-Size Threshold Circuits for Matrix Multiplication

Boolean circuits of McCulloch-Pitts threshold gates are a classic model of neural computation studied heavily in the late 20th century as a model of general computation. Recent advances in large-scale neural computing hardware has made their practical implementation a near-term possibility. We describe a theoretical approach for multiplying two $N$ by $N$ matrices that integrates threshold gate logic with conventional fast matrix multiplication algorithms, that perform $O(N^\omega)$ arithmetic operations for a positive constant $\omega < 3$. Our approach converts such a fast matrix multiplication algorithm into a constant-depth threshold circuit with approximately $O(N^\omega)$ gates. Prior to our work, it was not known whether the $\Theta(N^3)$-gate barrier for matrix multiplication was surmountable by constant-depth threshold circuits. Dense matrix multiplication is a core operation in convolutional neural network training. Performing this work on a neural architecture instead of off-loading it to a GPU may be an appealing option.