Neuromorphic scaling advantages for energy-efficient random walk computation

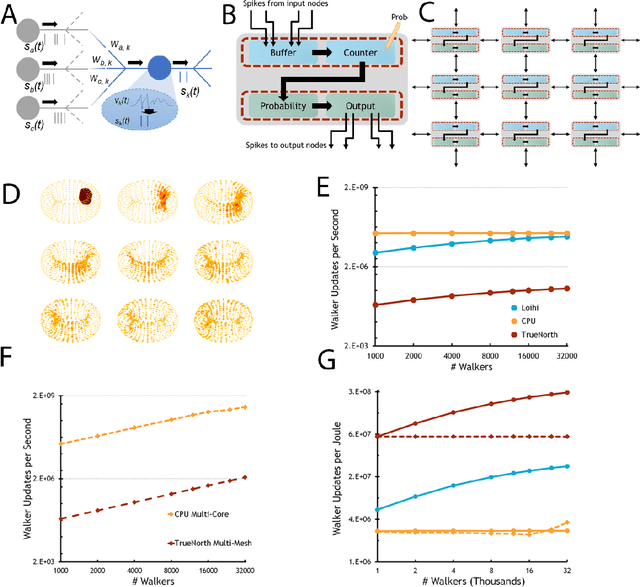
Computing stands to be radically improved by neuromorphic computing (NMC) approaches inspired by the brain's incredible efficiency and capabilities. Most NMC research, which aims to replicate the brain's computational structure and architecture in man-made hardware, has focused on artificial intelligence; however, less explored is whether this brain-inspired hardware can provide value beyond cognitive tasks. We demonstrate that high-degree parallelism and configurability of spiking neuromorphic architectures makes them well-suited to implement random walks via discrete time Markov chains. Such random walks are useful in Monte Carlo methods, which represent a fundamental computational tool for solving a wide range of numerical computing tasks. Additionally, we show how the mathematical basis for a probabilistic solution involving a class of stochastic differential equations can leverage those simulations to provide solutions for a range of broadly applicable computational tasks. Despite being in an early development stage, we find that NMC platforms, at a sufficient scale, can drastically reduce the energy demands of high-performance computing (HPC) platforms.

Constant-Depth and Subcubic-Size Threshold Circuits for Matrix Multiplication

Boolean circuits of McCulloch-Pitts threshold gates are a classic model of neural computation studied heavily in the late 20th century as a model of general computation. Recent advances in large-scale neural computing hardware has made their practical implementation a near-term possibility. We describe a theoretical approach for multiplying two $N$ by $N$ matrices that integrates threshold gate logic with conventional fast matrix multiplication algorithms, that perform $O(N^\omega)$ arithmetic operations for a positive constant $\omega < 3$. Our approach converts such a fast matrix multiplication algorithm into a constant-depth threshold circuit with approximately $O(N^\omega)$ gates. Prior to our work, it was not known whether the $\Theta(N^3)$-gate barrier for matrix multiplication was surmountable by constant-depth threshold circuits. Dense matrix multiplication is a core operation in convolutional neural network training. Performing this work on a neural architecture instead of off-loading it to a GPU may be an appealing option.

Spiking Neural Algorithms for Markov Process Random Walk

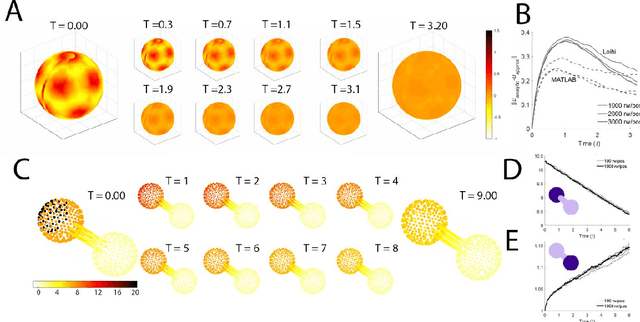
The random walk is a fundamental stochastic process that underlies many numerical tasks in scientific computing applications. We consider here two neural algorithms that can be used to efficiently implement random walks on spiking neuromorphic hardware. The first method tracks the positions of individual walkers independently by using a modular code inspired by the grid cell spatial representation in the brain. The second method tracks the densities of random walkers at each spatial location directly. We analyze the scaling complexity of each of these methods and illustrate their ability to model random walkers under different probabilistic conditions.