Solving Sparse Finite Element Problems on Neuromorphic Hardware

We demonstrate that scalable neuromorphic hardware can implement the finite element method, which is a critical numerical method for engineering and scientific discovery. Our approach maps the sparse interactions between neighboring finite elements to small populations of neurons that dynamically update according to the governing physics of a desired problem description. We show that for the Poisson equation, which describes many physical systems such as gravitational and electrostatic fields, this cortical-inspired neural circuit can achieve comparable levels of numerical accuracy and scaling while enabling the use of inherently parallel and energy-efficient neuromorphic hardware. We demonstrate that this approach can be used on the Intel Loihi 2 platform and illustrate how this approach can be extended to nontrivial mesh geometries and dynamics.

Decomposing spiking neural networks with Graphical Neural Activity Threads

A satisfactory understanding of information processing in spiking neural networks requires appropriate computational abstractions of neural activity. Traditionally, the neural population state vector has been the most common abstraction applied to spiking neural networks, but this requires artificially partitioning time into bins that are not obviously relevant to the network itself. We introduce a distinct set of techniques for analyzing spiking neural networks that decomposes neural activity into multiple, disjoint, parallel threads of activity. We construct these threads by estimating the degree of causal relatedness between pairs of spikes, then use these estimates to construct a directed acyclic graph that traces how the network activity evolves through individual spikes. We find that this graph of spiking activity naturally decomposes into disjoint connected components that overlap in space and time, which we call Graphical Neural Activity Threads (GNATs). We provide an efficient algorithm for finding analogous threads that reoccur in large spiking datasets, revealing that seemingly distinct spike trains are composed of similar underlying threads of activity, a hallmark of compositionality. The picture of spiking neural networks provided by our GNAT analysis points to new abstractions for spiking neural computation that are naturally adapted to the spatiotemporally distributed dynamics of spiking neural networks.

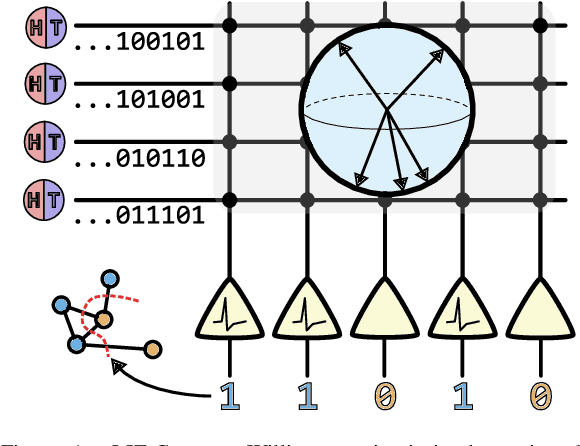
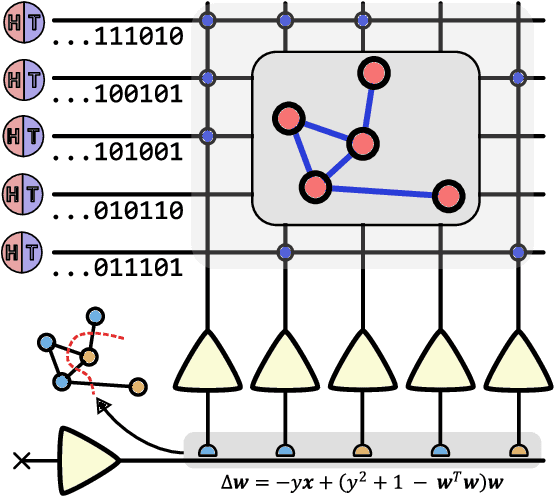
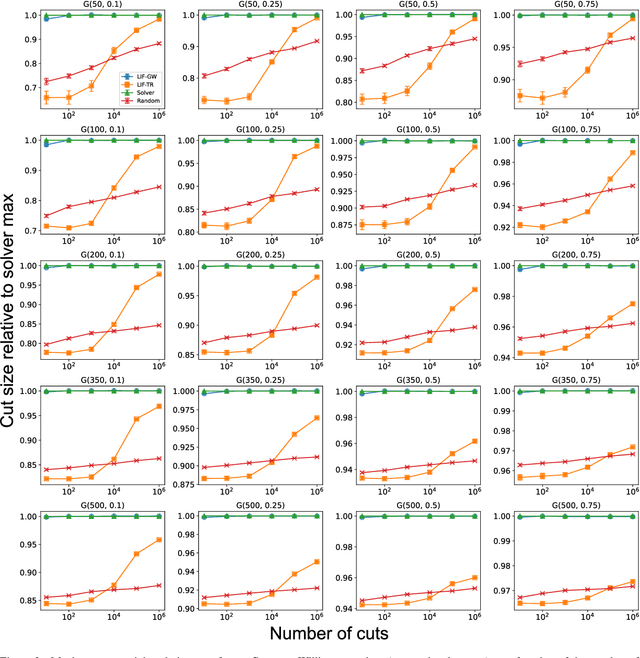
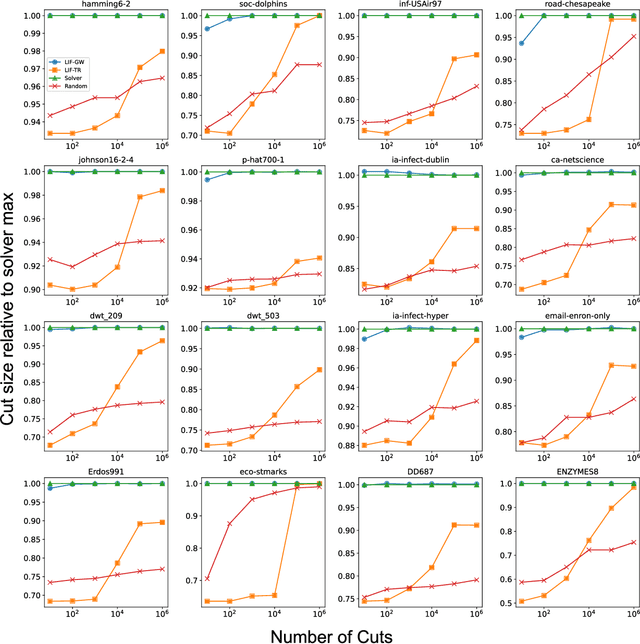
Stochastic Neuromorphic Circuits for Solving MAXCUT

Finding the maximum cut of a graph (MAXCUT) is a classic optimization problem that has motivated parallel algorithm development. While approximate algorithms to MAXCUT offer attractive theoretical guarantees and demonstrate compelling empirical performance, such approximation approaches can shift the dominant computational cost to the stochastic sampling operations. Neuromorphic computing, which uses the organizing principles of the nervous system to inspire new parallel computing architectures, offers a possible solution. One ubiquitous feature of natural brains is stochasticity: the individual elements of biological neural networks possess an intrinsic randomness that serves as a resource enabling their unique computational capacities. By designing circuits and algorithms that make use of randomness similarly to natural brains, we hypothesize that the intrinsic randomness in microelectronics devices could be turned into a valuable component of a neuromorphic architecture enabling more efficient computations. Here, we present neuromorphic circuits that transform the stochastic behavior of a pool of random devices into useful correlations that drive stochastic solutions to MAXCUT. We show that these circuits perform favorably in comparison to software solvers and argue that this neuromorphic hardware implementation provides a path for scaling advantages. This work demonstrates the utility of combining neuromorphic principles with intrinsic randomness as a computational resource for new computational architectures.