Emergent behavior and neural dynamics in artificial agents tracking turbulent plumes

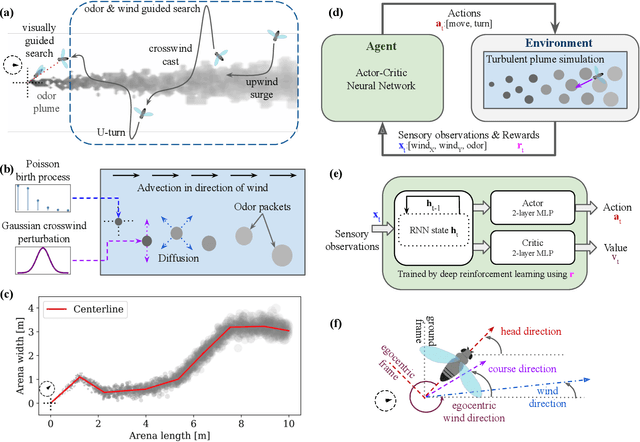
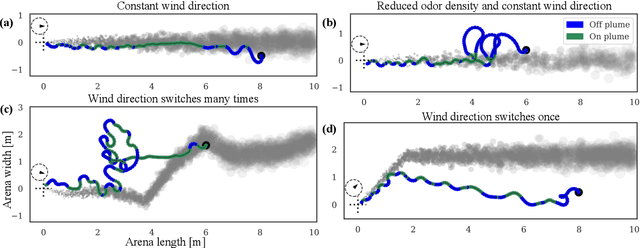
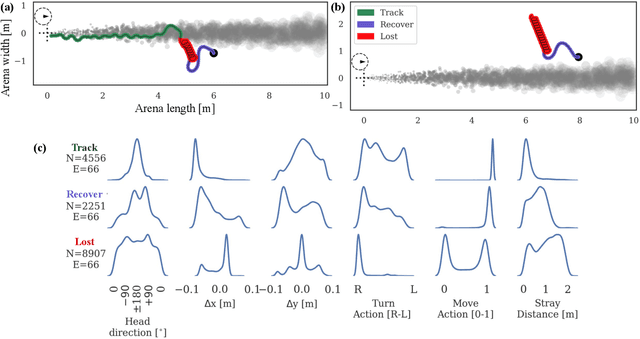
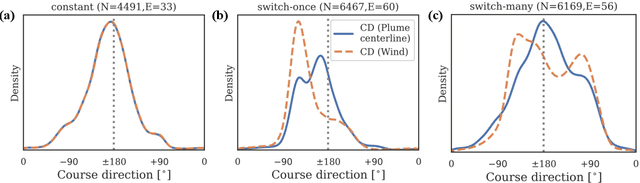
Tracking a turbulent plume to locate its source is a complex control problem because it requires multi-sensory integration and must be robust to intermittent odors, changing wind direction, and variable plume statistics. This task is routinely performed by flying insects, often over long distances, in pursuit of food or mates. Several aspects of this remarkable behavior have been studied in detail in many experimental studies. Here, we take a complementary in silico approach, using artificial agents trained with reinforcement learning to develop an integrated understanding of the behaviors and neural computations that support plume tracking. Specifically, we use deep reinforcement learning (DRL) to train recurrent neural network (RNN) agents to locate the source of simulated turbulent plumes. Interestingly, the agents' emergent behaviors resemble those of flying insects, and the RNNs learn to represent task-relevant variables, such as head direction and time since last odor encounter. Our analyses suggest an intriguing experimentally testable hypothesis for tracking plumes in changing wind direction -- that agents follow local plume shape rather than the current wind direction. While reflexive short-memory behaviors are sufficient for tracking plumes in constant wind, longer timescales of memory are essential for tracking plumes that switch direction. At the level of neural dynamics, the RNNs' population activity is low-dimensional and organized into distinct dynamical structures, with some correspondence to behavioral modules. Our in silico approach provides key intuitions for turbulent plume tracking strategies and motivates future targeted experimental and theoretical developments.

Time-varying Autoregression with Low Rank Tensors

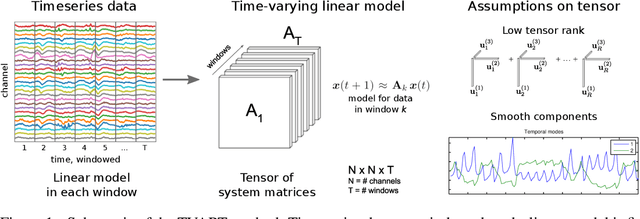
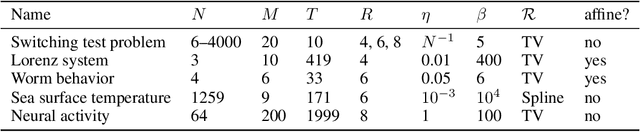
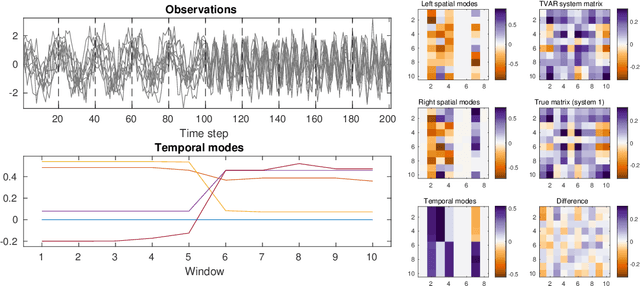
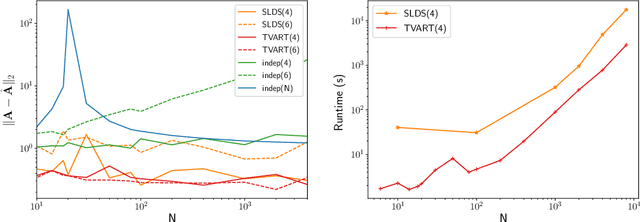
We present a windowed technique to learn parsimonious time-varying autoregressive models from multivariate timeseries. This unsupervised method uncovers spatiotemporal structure in data via non-smooth and non-convex optimization. In each time window, we assume the data follow a linear model parameterized by a potentially different system matrix, and we model this stack of system matrices as a low rank tensor. Because of its structure, the model is scalable to high-dimensional data and can easily incorporate priors such as smoothness over time. We find the components of the tensor using alternating minimization and prove that any stationary point of this algorithm is a local minimum. In a test case, our method identifies the true rank of a switching linear system in the presence of noise. We illustrate our model's utility and superior scalability over extant methods when applied to several synthetic and real examples, including a nonlinear dynamical system, worm behavior, sea surface temperature, and monkey brain recordings.