FC2T2: The Fast Continuous Convolutional Taylor Transform with Applications in Vision and Graphics

Series expansions have been a cornerstone of applied mathematics and engineering for centuries. In this paper, we revisit the Taylor series expansion from a modern Machine Learning perspective. Specifically, we introduce the Fast Continuous Convolutional Taylor Transform (FC2T2), a variant of the Fast Multipole Method (FMM), that allows for the efficient approximation of low dimensional convolutional operators in continuous space. We build upon the FMM which is an approximate algorithm that reduces the computational complexity of N-body problems from O(NM) to O(N+M) and finds application in e.g. particle simulations. As an intermediary step, the FMM produces a series expansion for every cell on a grid and we introduce algorithms that act directly upon this representation. These algorithms analytically but approximately compute the quantities required for the forward and backward pass of the backpropagation algorithm and can therefore be employed as (implicit) layers in Neural Networks. Specifically, we introduce a root-implicit layer that outputs surface normals and object distances as well as an integral-implicit layer that outputs a rendering of a radiance field given a 3D pose. In the context of Machine Learning, $N$ and $M$ can be understood as the number of model parameters and model evaluations respectively which entails that, for applications that require repeated function evaluations which are prevalent in Computer Vision and Graphics, unlike regular Neural Networks, the techniques introduce in this paper scale gracefully with parameters. For some applications, this results in a 200x reduction in FLOPs compared to state-of-the-art approaches at a reasonable or non-existent loss in accuracy.

Deep Probabilistic Koopman: Long-term time-series forecasting under periodic uncertainties

Probabilistic forecasting of complex phenomena is paramount to various scientific disciplines and applications. Despite the generality and importance of the problem, general mathematical techniques that allow for stable long-term forecasts with calibrated uncertainty measures are lacking. For most time series models, the difficulty of obtaining accurate probabilistic future time step predictions increases with the prediction horizon. In this paper, we introduce a surprisingly simple approach that characterizes time-varying distributions and enables reasonably accurate predictions thousands of timesteps into the future. This technique, which we call Deep Probabilistic Koopman (DPK), is based on recent advances in linear Koopman operator theory, and does not require time stepping for future time predictions. Koopman models also tend to have a small parameter footprint (often less than 10,000 parameters). We demonstrate the long-term forecasting performance of these models on a diversity of domains, including electricity demand forecasting, atmospheric chemistry, and neuroscience. For electricity demand modeling, our domain-agnostic technique outperforms all of 177 domain-specific competitors in the most recent Global Energy Forecasting Competition.

Learning to Solve AC Optimal Power Flow by Differentiating through Holomorphic Embeddings

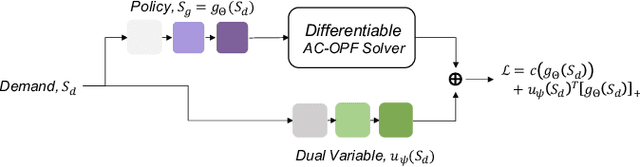
Alternating current optimal power flow (AC-OPF) is one of the fundamental problems in power systems operation. AC-OPF is traditionally cast as a constrained optimization problem that seeks optimal generation set points whilst fulfilling a set of non-linear equality constraints -- the power flow equations. With increasing penetration of renewable generation, grid operators need to solve larger problems at shorter intervals. This motivates the research interest in learning OPF solutions with neural networks, which have fast inference time and is potentially scalable to large networks. The main difficulty in solving the AC-OPF problem lies in dealing with this equality constraint that has spurious roots, i.e. there are assignments of voltages that fulfill the power flow equations that however are not physically realizable. This property renders any method relying on projected-gradients brittle because these non-physical roots can act as attractors. In this paper, we show efficient strategies that circumvent this problem by differentiating through the operations of a power flow solver that embeds the power flow equations into a holomorphic function. The resulting learning-based approach is validated experimentally on a 200-bus system and we show that, after training, the learned agent produces optimized power flow solutions reliably and fast. Specifically, we report a 12x increase in speed and a 40% increase in robustness compared to a traditional solver. To the best of our knowledge, this approach constitutes the first learning-based approach that successfully respects the full non-linear AC-OPF equations.

From Fourier to Koopman: Spectral Methods for Long-term Time Series Prediction

We propose spectral methods for long-term forecasting of temporal signals stemming from linear and nonlinear quasi-periodic dynamical systems. For linear signals, we introduce an algorithm with similarities to the Fourier transform but which does not rely on periodicity assumptions, allowing for forecasting given potentially arbitrary sampling intervals. We then extend this algorithm to handle nonlinearities by leveraging Koopman theory. The resulting algorithm performs a spectral decomposition in a nonlinear, data-dependent basis. The optimization objective for both algorithms is highly non-convex. However, expressing the objective in the frequency domain allows us to compute global optima of the error surface in a scalable and efficient manner, partially by exploiting the computational properties of the Fast Fourier Transform. Because of their close relation to Bayesian Spectral Analysis, uncertainty quantification metrics are a natural byproduct of the spectral forecasting methods. We extensively benchmark these algorithms against other leading forecasting methods on a range of synthetic experiments as well as in the context of real-world power systems and fluid flows.