Splitting physics-informed neural networks for inferring the dynamics of integer- and fractional-order neuron models

We introduce a new approach for solving forward systems of differential equations using a combination of splitting methods and physics-informed neural networks (PINNs). The proposed method, splitting PINN, effectively addresses the challenge of applying PINNs to forward dynamical systems and demonstrates improved accuracy through its application to neuron models. Specifically, we apply operator splitting to decompose the original neuron model into sub-problems that are then solved using PINNs. Moreover, we develop an $L^1$ scheme for discretizing fractional derivatives in fractional neuron models, leading to improved accuracy and efficiency. The results of this study highlight the potential of splitting PINNs in solving both integer- and fractional-order neuron models, as well as other similar systems in computational science and engineering.

PIAT: Physics Informed Adversarial Training for Solving Partial Differential Equations

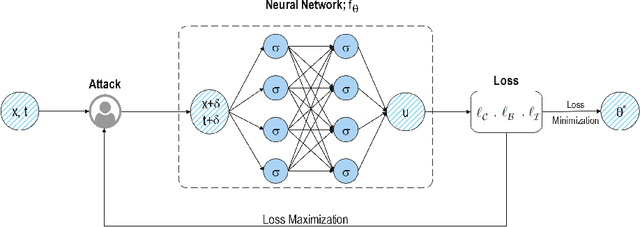
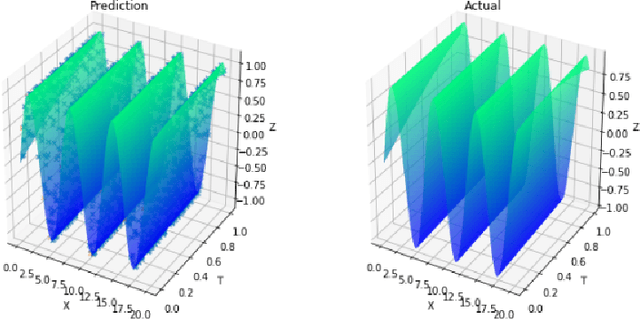
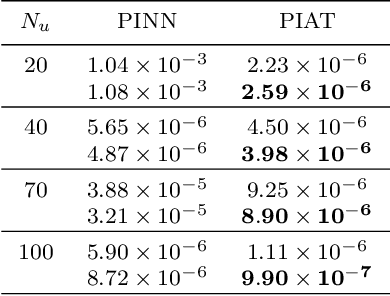
In this paper, we propose the physics informed adversarial training (PIAT) of neural networks for solving nonlinear differential equations (NDE). It is well-known that the standard training of neural networks results in non-smooth functions. Adversarial training (AT) is an established defense mechanism against adversarial attacks, which could also help in making the solution smooth. AT include augmenting the training mini-batch with a perturbation that makes the network output mismatch the desired output adversarially. Unlike formal AT, which relies only on the training data, here we encode the governing physical laws in the form of nonlinear differential equations using automatic differentiation in the adversarial network architecture. We compare PIAT with PINN to indicate the effectiveness of our method in solving NDEs for up to 10 dimensions. Moreover, we propose weight decay and Gaussian smoothing to demonstrate the PIAT advantages. The code repository is available at https://github.com/rohban-lab/PIAT.