STONet: A novel neural operator for modeling solute transport in micro-cracked reservoirs

In this work, we develop a novel neural operator, the Solute Transport Operator Network (STONet), to efficiently model contaminant transport in micro-cracked reservoirs. The model combines different networks to encode heterogeneous properties effectively. By predicting the concentration rate, we are able to accurately model the transport process. Numerical experiments demonstrate that our neural operator approach achieves accuracy comparable to that of the finite element method. The previously introduced Enriched DeepONet architecture has been revised, motivated by the architecture of the popular multi-head attention of transformers, to improve its performance without increasing the compute cost. The computational efficiency of the proposed model enables rapid and accurate predictions of solute transport, facilitating the optimization of reservoir management strategies and the assessment of environmental impacts. The data and code for the paper will be published at https://github.com/ehsanhaghighat/STONet.

Inverse modeling of nonisothermal multiphase poromechanics using physics-informed neural networks

We propose a solution strategy for parameter identification in multiphase thermo-hydro-mechanical (THM) processes in porous media using physics-informed neural networks (PINNs). We employ a dimensionless form of the THM governing equations that is particularly well suited for the inverse problem, and we leverage the sequential multiphysics PINN solver we developed in previous work. We validate the proposed inverse-modeling approach on multiple benchmark problems, including Terzaghi's isothermal consolidation problem, Barry-Mercer's isothermal injection-production problem, and nonisothermal consolidation of an unsaturated soil layer. We report the excellent performance of the proposed sequential PINN-THM inverse solver, thus paving the way for the application of PINNs to inverse modeling of complex nonlinear multiphysics problems.

Physics-informed neural network solution of thermo-hydro-mechanical (THM) processes in porous media

Physics-Informed Neural Networks (PINNs) have received increased interest for forward, inverse, and surrogate modeling of problems described by partial differential equations (PDE). However, their application to multiphysics problem, governed by several coupled PDEs, present unique challenges that have hindered the robustness and widespread applicability of this approach. Here we investigate the application of PINNs to the forward solution of problems involving thermo-hydro-mechanical (THM) processes in porous media, which exhibit disparate spatial and temporal scales in thermal conductivity, hydraulic permeability, and elasticity. In addition, PINNs are faced with the challenges of the multi-objective and non-convex nature of the optimization problem. To address these fundamental issues, we: (1)~rewrite the THM governing equations in dimensionless form that is best suited for deep-learning algorithms; (2)~propose a sequential training strategy that circumvents the need for a simultaneous solution of the multiphysics problem and facilitates the task of optimizers in the solution search; and (3)~leverage adaptive weight strategies to overcome the stiffness in the gradient flow of the multi-objective optimization problem. Finally, we apply this framework to the solution of several synthetic problems in 1D and~2D.

Physics-informed neural network simulation of multiphase poroelasticity using stress-split sequential training

Physics-informed neural networks (PINNs) have received significant attention as a unified framework for forward, inverse, and surrogate modeling of problems governed by partial differential equations (PDEs). Training PINNs for forward problems, however, pose significant challenges, mainly because of the complex non-convex and multi-objective loss function. In this work, we present a PINN approach to solving the equations of coupled flow and deformation in porous media for both single-phase and multiphase flow. To this end, we construct the solution space using multi-layer neural networks. Due to the dynamics of the problem, we find that incorporating multiple differential relations into the loss function results in an unstable optimization problem, meaning that sometimes it converges to the trivial null solution, other times it moves very far from the expected solution. We report a dimensionless form of the coupled governing equations that we find most favourable to the optimizer. Additionally, we propose a sequential training approach based on the stress-split algorithms of poromechanics. Notably, we find that sequential training based on stress-split performs well for different problems, while the classical strain-split algorithm shows an unstable behaviour similar to what is reported in the context of finite element solvers. We use the approach to solve benchmark problems of poroelasticity, including Mandel's consolidation problem, Barry-Mercer's injection-production problem, and a reference two-phase drainage problem. The Python-SciANN codes reproducing the results reported in this manuscript will be made publicly available at https://github.com/sciann/sciann-applications.

Deep learning for solution and inversion of structural mechanics and vibrations

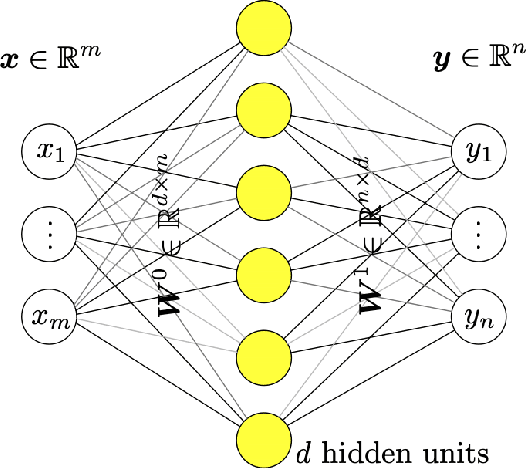
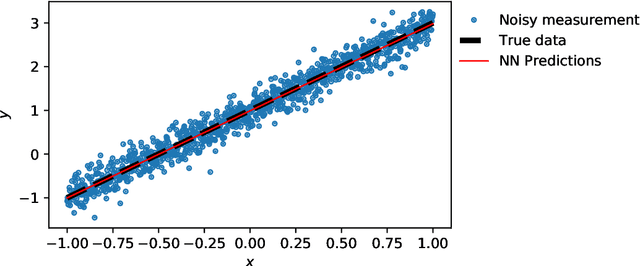
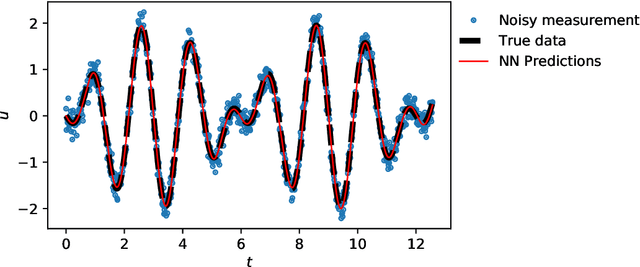
Deep learning has been the most popular machine learning method in the last few years. In this chapter, we present the application of deep learning and physics-informed neural networks concerning structural mechanics and vibration problems. Demonstration problems involve de-noising data, solution to time-dependent ordinary and partial differential equations, and characterizing the system's response for a given data.

A nonlocal physics-informed deep learning framework using the peridynamic differential operator

The Physics-Informed Neural Network (PINN) framework introduced recently incorporates physics into deep learning, and offers a promising avenue for the solution of partial differential equations (PDEs) as well as identification of the equation parameters. The performance of existing PINN approaches, however, may degrade in the presence of sharp gradients, as a result of the inability of the network to capture the solution behavior globally. We posit that this shortcoming may be remedied by introducing long-range (nonlocal) interactions into the network's input, in addition to the short-range (local) space and time variables. Following this ansatz, here we develop a nonlocal PINN approach using the Peridynamic Differential Operator (PDDO)---a numerical method which incorporates long-range interactions and removes spatial derivatives in the governing equations. Because the PDDO functions can be readily incorporated in the neural network architecture, the nonlocality does not degrade the performance of modern deep-learning algorithms. We apply nonlocal PDDO-PINN to the solution and identification of material parameters in solid mechanics and, specifically, to elastoplastic deformation in a domain subjected to indentation by a rigid punch, for which the mixed displacement--traction boundary condition leads to localized deformation and sharp gradients in the solution. We document the superior behavior of nonlocal PINN with respect to local PINN in both solution accuracy and parameter inference, illustrating its potential for simulation and discovery of partial differential equations whose solution develops sharp gradients.

SciANN: A Keras wrapper for scientific computations and physics-informed deep learning using artificial neural networks

In this paper, we introduce SciANN, a Python package for scientific computing and physics-informed deep learning using artificial neural networks. SciANN uses the widely used deep-learning packages Tensorflow and Keras to build deep neural networks and optimization models, thus inheriting many of Keras's functionalities, such as batch optimization and model reuse for transfer learning. SciANN is designed to abstract neural network construction for scientific computations and solution and discovery of partial differential equations (PDE) using the physics-informed neural networks (PINN) architecture, therefore providing the flexibility to set up complex functional forms. We illustrate, in a series of examples, how the framework can be used for curve fitting on discrete data, and for solution and discovery of PDEs in strong and weak forms. We summarize the features currently available in SciANN, and also outline ongoing and future developments.

A deep learning framework for solution and discovery in solid mechanics: linear elasticity

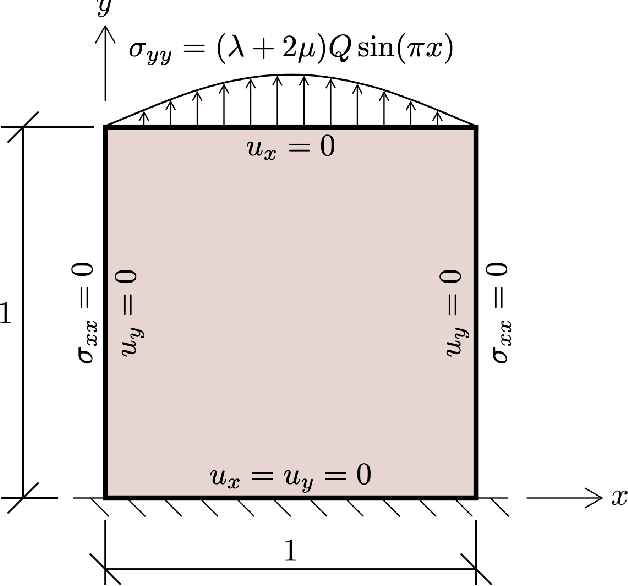
We present the application of a class of deep learning, known as Physics Informed Neural Networks (PINN), to learning and discovery in solid mechanics. We explain how to incorporate the momentum balance and constitutive relations into PINN, and explore in detail the application to linear elasticity, although the framework is rather general and can be extended to other solid-mechanics problems. While common PINN algorithms are based on training one deep neural network (DNN), we propose a multi-network model that results in more accurate representation of the field variables. To validate the model, we test the framework on synthetic data generated from analytical and numerical reference solutions. We study convergence of the PINN model, and show that Isogeometric Analysis (IGA) results in superior accuracy and convergence characteristics compared with classic low-order Finite Element Method (FEM). We also show the applicability of the framework for transfer learning, and find vastly accelerated convergence during network re-training. Finally, we find that honoring the physics leads to improved robustness: when trained only on a few parameters, we find that the PINN model can accurately predict the solution for a wide range of parameters new to the network---thus pointing to an important application of this framework to sensitivity analysis and surrogate modeling.