Patient-specific, mechanistic models of tumor growth incorporating artificial intelligence and big data

Despite the remarkable advances in cancer diagnosis, treatment, and management that have occurred over the past decade, malignant tumors remain a major public health problem. Further progress in combating cancer may be enabled by personalizing the delivery of therapies according to the predicted response for each individual patient. The design of personalized therapies requires patient-specific information integrated into an appropriate mathematical model of tumor response. A fundamental barrier to realizing this paradigm is the current lack of a rigorous, yet practical, mathematical theory of tumor initiation, development, invasion, and response to therapy. In this review, we begin by providing an overview of different approaches to modeling tumor growth and treatment, including mechanistic as well as data-driven models based on ``big data" and artificial intelligence. Next, we present illustrative examples of mathematical models manifesting their utility and discussing the limitations of stand-alone mechanistic and data-driven models. We further discuss the potential of mechanistic models for not only predicting, but also optimizing response to therapy on a patient-specific basis. We then discuss current efforts and future possibilities to integrate mechanistic and data-driven models. We conclude by proposing five fundamental challenges that must be addressed to fully realize personalized care for cancer patients driven by computational models.

A deep learning framework for solution and discovery in solid mechanics: linear elasticity

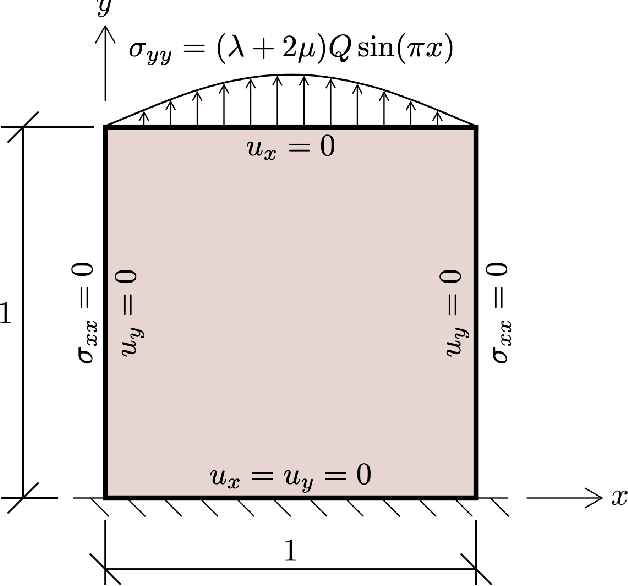
We present the application of a class of deep learning, known as Physics Informed Neural Networks (PINN), to learning and discovery in solid mechanics. We explain how to incorporate the momentum balance and constitutive relations into PINN, and explore in detail the application to linear elasticity, although the framework is rather general and can be extended to other solid-mechanics problems. While common PINN algorithms are based on training one deep neural network (DNN), we propose a multi-network model that results in more accurate representation of the field variables. To validate the model, we test the framework on synthetic data generated from analytical and numerical reference solutions. We study convergence of the PINN model, and show that Isogeometric Analysis (IGA) results in superior accuracy and convergence characteristics compared with classic low-order Finite Element Method (FEM). We also show the applicability of the framework for transfer learning, and find vastly accelerated convergence during network re-training. Finally, we find that honoring the physics leads to improved robustness: when trained only on a few parameters, we find that the PINN model can accurately predict the solution for a wide range of parameters new to the network---thus pointing to an important application of this framework to sensitivity analysis and surrogate modeling.