Patient-specific, mechanistic models of tumor growth incorporating artificial intelligence and big data

Despite the remarkable advances in cancer diagnosis, treatment, and management that have occurred over the past decade, malignant tumors remain a major public health problem. Further progress in combating cancer may be enabled by personalizing the delivery of therapies according to the predicted response for each individual patient. The design of personalized therapies requires patient-specific information integrated into an appropriate mathematical model of tumor response. A fundamental barrier to realizing this paradigm is the current lack of a rigorous, yet practical, mathematical theory of tumor initiation, development, invasion, and response to therapy. In this review, we begin by providing an overview of different approaches to modeling tumor growth and treatment, including mechanistic as well as data-driven models based on ``big data" and artificial intelligence. Next, we present illustrative examples of mathematical models manifesting their utility and discussing the limitations of stand-alone mechanistic and data-driven models. We further discuss the potential of mechanistic models for not only predicting, but also optimizing response to therapy on a patient-specific basis. We then discuss current efforts and future possibilities to integrate mechanistic and data-driven models. We conclude by proposing five fundamental challenges that must be addressed to fully realize personalized care for cancer patients driven by computational models.

An untrained deep learning method for reconstructing dynamic magnetic resonance images from accelerated model-based data

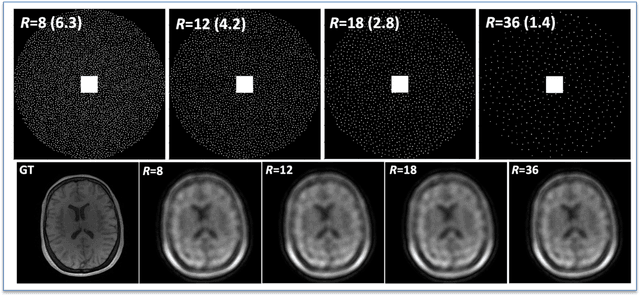
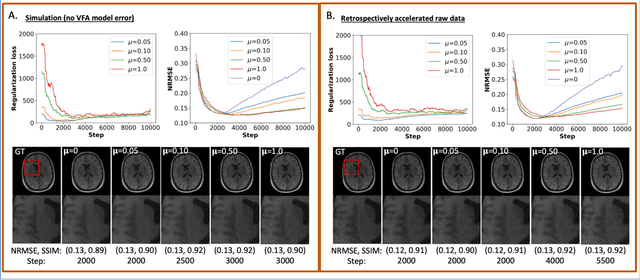
The purpose of this work is to implement physics-based regularization as a stopping condition in tuning an untrained deep neural network for reconstructing MR images from accelerated data. The ConvDecoder neural network was trained with a physics-based regularization term incorporating the spoiled gradient echo equation that describes variable-flip angle (VFA) data. Fully-sampled VFA k-space data were retrospectively accelerated by factors of R={8,12,18,36} and reconstructed with ConvDecoder (CD), ConvDecoder with the proposed regularization (CD+r), locally low-rank (LR) reconstruction, and compressed sensing with L1-wavelet regularization (L1). Final images from CD+r training were evaluated at the \emph{argmin} of the regularization loss; whereas the CD, LR, and L1 reconstructions were chosen optimally based on ground truth data. The performance measures used were the normalized root-mean square error, the concordance correlation coefficient (CCC), and the structural similarity index (SSIM). The CD+r reconstructions, chosen using the stopping condition, yielded SSIMs that were similar to the CD (p=0.47) and LR SSIMs (p=0.95) across R and that were significantly higher than the L1 SSIMs (p=0.04). The CCC values for the CD+r T1 maps across all R and subjects were greater than those corresponding to the L1 (p=0.15) and LR (p=0.13) T1 maps, respectively. For R > 12 (<4.2 minutes scan time), L1 and LR T1 maps exhibit a loss of spatially refined details compared to CD+r. We conclude that the use of an untrained neural network together with a physics-based regularization loss shows promise as a measure for determining the optimal stopping point in training without relying on fully-sampled ground truth data.