Viraj Wadhwa
An untrained deep learning method for reconstructing dynamic magnetic resonance images from accelerated model-based data
May 04, 2022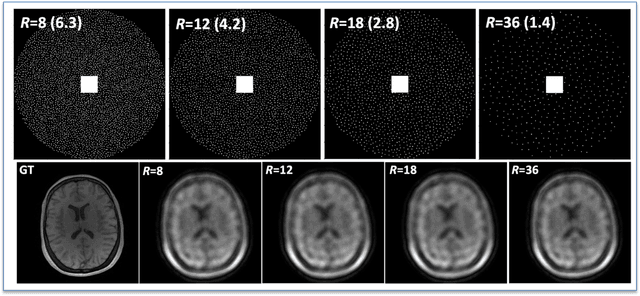

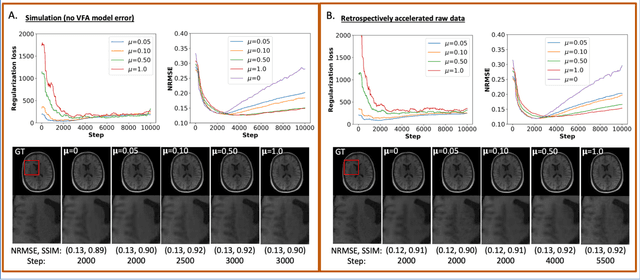

Abstract:The purpose of this work is to implement physics-based regularization as a stopping condition in tuning an untrained deep neural network for reconstructing MR images from accelerated data. The ConvDecoder neural network was trained with a physics-based regularization term incorporating the spoiled gradient echo equation that describes variable-flip angle (VFA) data. Fully-sampled VFA k-space data were retrospectively accelerated by factors of R={8,12,18,36} and reconstructed with ConvDecoder (CD), ConvDecoder with the proposed regularization (CD+r), locally low-rank (LR) reconstruction, and compressed sensing with L1-wavelet regularization (L1). Final images from CD+r training were evaluated at the \emph{argmin} of the regularization loss; whereas the CD, LR, and L1 reconstructions were chosen optimally based on ground truth data. The performance measures used were the normalized root-mean square error, the concordance correlation coefficient (CCC), and the structural similarity index (SSIM). The CD+r reconstructions, chosen using the stopping condition, yielded SSIMs that were similar to the CD (p=0.47) and LR SSIMs (p=0.95) across R and that were significantly higher than the L1 SSIMs (p=0.04). The CCC values for the CD+r T1 maps across all R and subjects were greater than those corresponding to the L1 (p=0.15) and LR (p=0.13) T1 maps, respectively. For R > 12 (<4.2 minutes scan time), L1 and LR T1 maps exhibit a loss of spatially refined details compared to CD+r. We conclude that the use of an untrained neural network together with a physics-based regularization loss shows promise as a measure for determining the optimal stopping point in training without relying on fully-sampled ground truth data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge