A solution for the mean parametrization of the von Mises-Fisher distribution

The von Mises-Fisher distribution as an exponential family can be expressed in terms of either its natural or its mean parameters. Unfortunately, however, the normalization function for the distribution in terms of its mean parameters is not available in closed form, limiting the practicality of the mean parametrization and complicating maximum-likelihood estimation more generally. We derive a second-order ordinary differential equation, the solution to which yields the mean-parameter normalizer along with its first two derivatives, as well as the variance function of the family. We also provide closed-form approximations to the solution of the differential equation. This allows rapid evaluation of both densities and natural parameters in terms of mean parameters. We show applications to topic modeling with mixtures of von Mises-Fisher distributions using Bregman Clustering.

Automatic Posterior Transformation for Likelihood-Free Inference

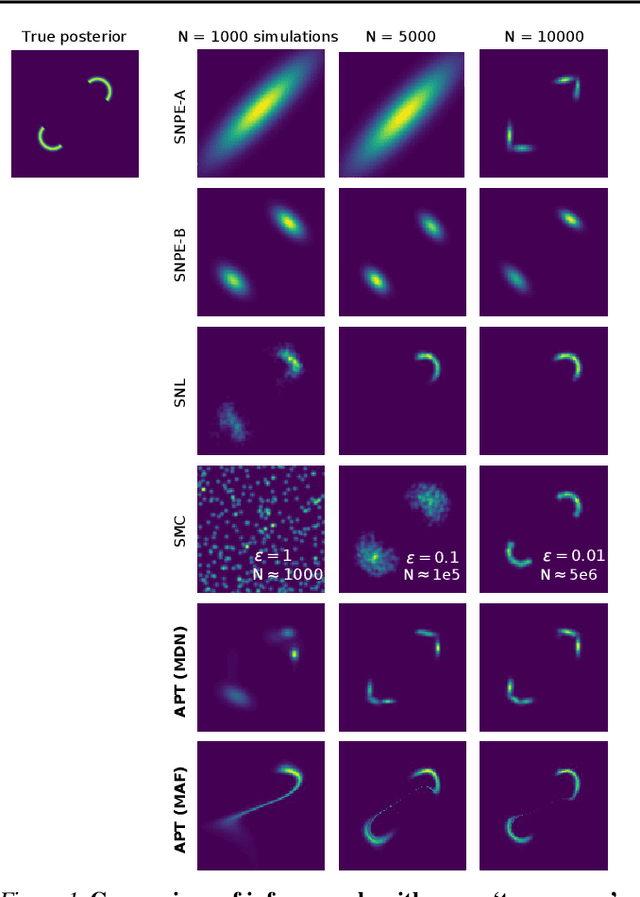
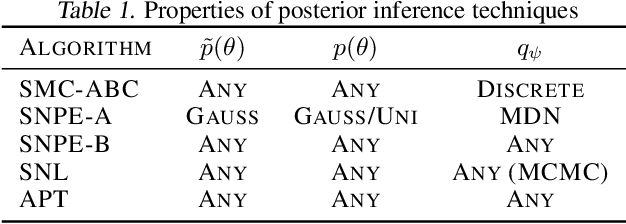
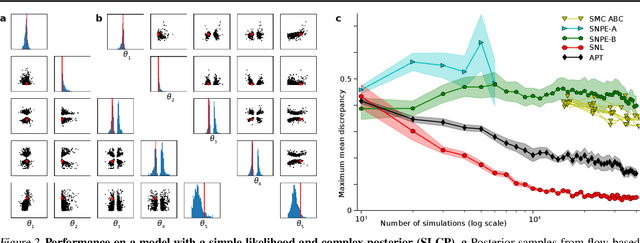
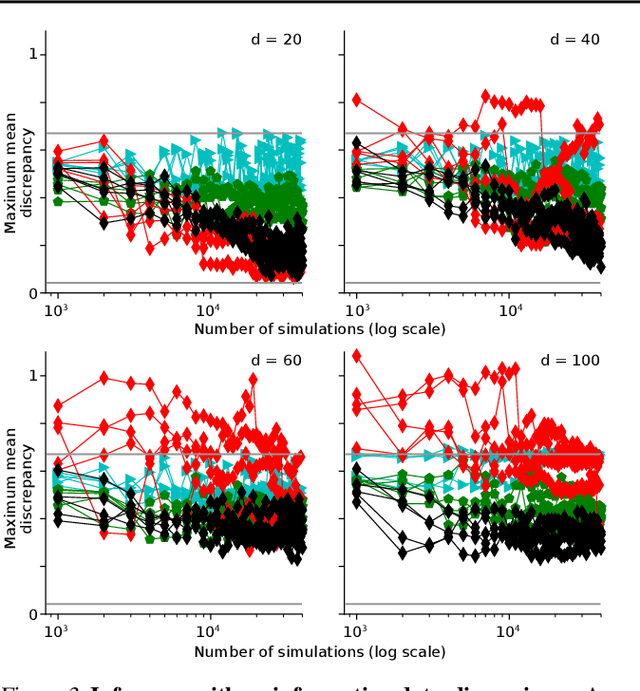
How can one perform Bayesian inference on stochastic simulators with intractable likelihoods? A recent approach is to learn the posterior from adaptively proposed simulations using neural network-based conditional density estimators. However, existing methods are limited to a narrow range of proposal distributions or require importance weighting that can limit performance in practice. Here we present automatic posterior transformation (APT), a new sequential neural posterior estimation method for simulation-based inference. APT can modify the posterior estimate using arbitrary, dynamically updated proposals, and is compatible with powerful flow-based density estimators. It is more flexible, scalable and efficient than previous simulation-based inference techniques. APT can operate directly on high-dimensional time series and image data, opening up new applications for likelihood-free inference.

Flexible statistical inference for mechanistic models of neural dynamics

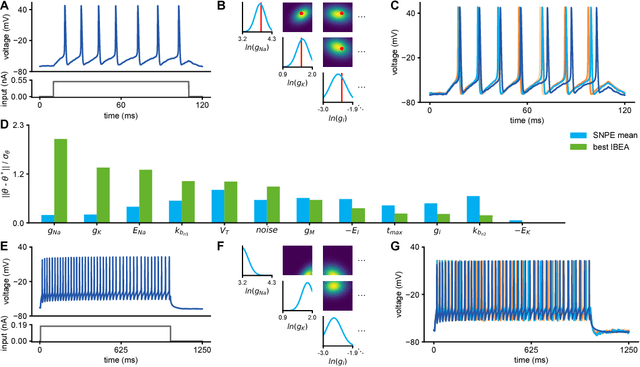
Mechanistic models of single-neuron dynamics have been extensively studied in computational neuroscience. However, identifying which models can quantitatively reproduce empirically measured data has been challenging. We propose to overcome this limitation by using likelihood-free inference approaches (also known as Approximate Bayesian Computation, ABC) to perform full Bayesian inference on single-neuron models. Our approach builds on recent advances in ABC by learning a neural network which maps features of the observed data to the posterior distribution over parameters. We learn a Bayesian mixture-density network approximating the posterior over multiple rounds of adaptively chosen simulations. Furthermore, we propose an efficient approach for handling missing features and parameter settings for which the simulator fails, as well as a strategy for automatically learning relevant features using recurrent neural networks. On synthetic data, our approach efficiently estimates posterior distributions and recovers ground-truth parameters. On in-vitro recordings of membrane voltages, we recover multivariate posteriors over biophysical parameters, which yield model-predicted voltage traces that accurately match empirical data. Our approach will enable neuroscientists to perform Bayesian inference on complex neuron models without having to design model-specific algorithms, closing the gap between mechanistic and statistical approaches to single-neuron modelling.

Extracting low-dimensional dynamics from multiple large-scale neural population recordings by learning to predict correlations

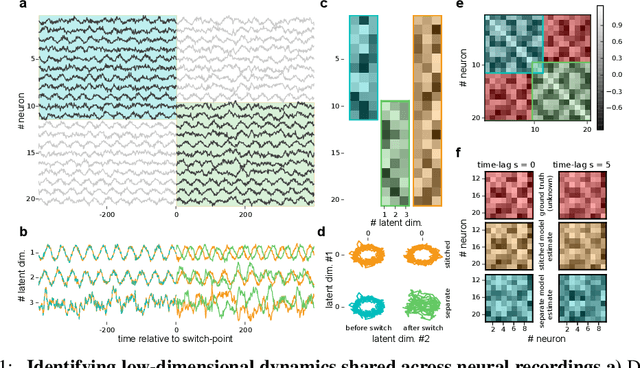
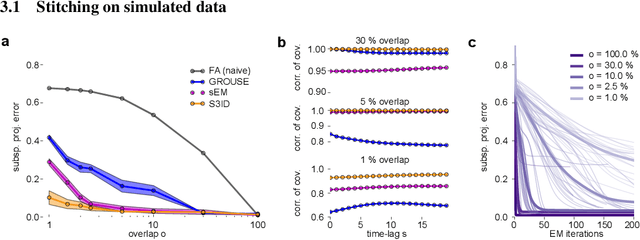
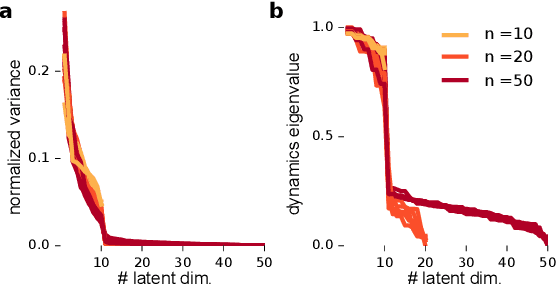
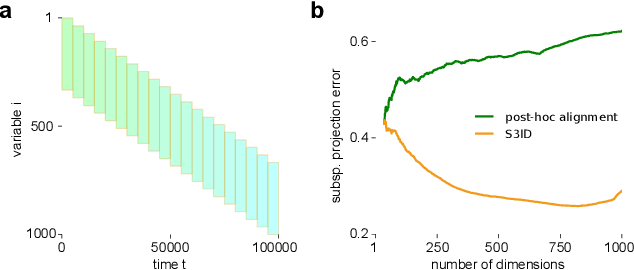
A powerful approach for understanding neural population dynamics is to extract low-dimensional trajectories from population recordings using dimensionality reduction methods. Current approaches for dimensionality reduction on neural data are limited to single population recordings, and can not identify dynamics embedded across multiple measurements. We propose an approach for extracting low-dimensional dynamics from multiple, sequential recordings. Our algorithm scales to data comprising millions of observed dimensions, making it possible to access dynamics distributed across large populations or multiple brain areas. Building on subspace-identification approaches for dynamical systems, we perform parameter estimation by minimizing a moment-matching objective using a scalable stochastic gradient descent algorithm: The model is optimized to predict temporal covariations across neurons and across time. We show how this approach naturally handles missing data and multiple partial recordings, and can identify dynamics and predict correlations even in the presence of severe subsampling and small overlap between recordings. We demonstrate the effectiveness of the approach both on simulated data and a whole-brain larval zebrafish imaging dataset.