Scientific Inference With Interpretable Machine Learning: Analyzing Models to Learn About Real-World Phenomena

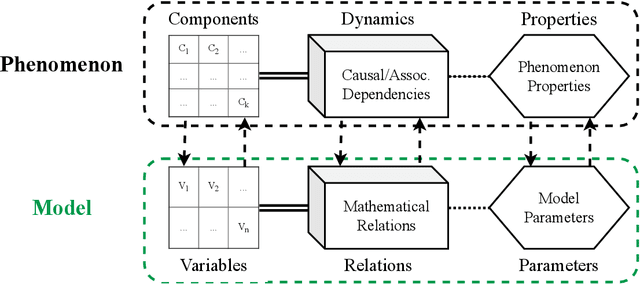
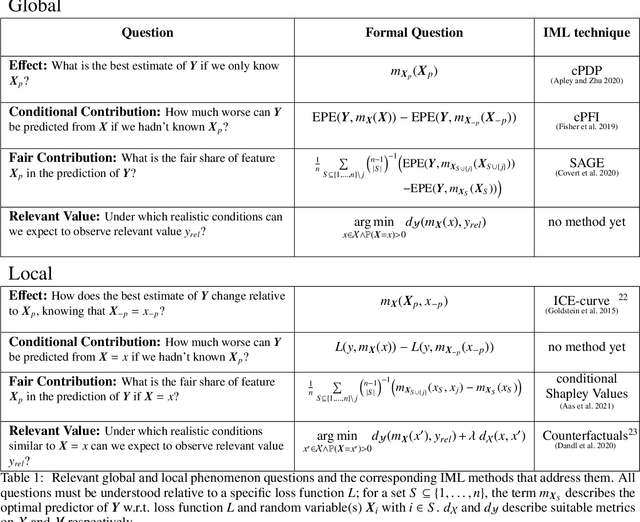
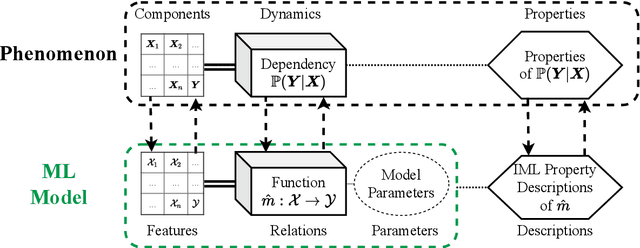
Interpretable machine learning (IML) is concerned with the behavior and the properties of machine learning models. Scientists, however, are only interested in the model as a gateway to understanding the modeled phenomenon. We show how to develop IML methods such that they allow insight into relevant phenomenon properties. We argue that current IML research conflates two goals of model-analysis -- model audit and scientific inference. Thereby, it remains unclear if model interpretations have corresponding phenomenon interpretation. Building on statistical decision theory, we show that ML model analysis allows to describe relevant aspects of the joint data probability distribution. We provide a five-step framework for constructing IML descriptors that can help in addressing scientific questions, including a natural way to quantify epistemic uncertainty. Our phenomenon-centric approach to IML in science clarifies: the opportunities and limitations of IML for inference; that conditional not marginal sampling is required; and, the conditions under which we can trust IML methods.

SBI -- A toolkit for simulation-based inference

Scientists and engineers employ stochastic numerical simulators to model empirically observed phenomena. In contrast to purely statistical models, simulators express scientific principles that provide powerful inductive biases, improve generalization to new data or scenarios and allow for fewer, more interpretable and domain-relevant parameters. Despite these advantages, tuning a simulator's parameters so that its outputs match data is challenging. Simulation-based inference (SBI) seeks to identify parameter sets that a) are compatible with prior knowledge and b) match empirical observations. Importantly, SBI does not seek to recover a single 'best' data-compatible parameter set, but rather to identify all high probability regions of parameter space that explain observed data, and thereby to quantify parameter uncertainty. In Bayesian terminology, SBI aims to retrieve the posterior distribution over the parameters of interest. In contrast to conventional Bayesian inference, SBI is also applicable when one can run model simulations, but no formula or algorithm exists for evaluating the probability of data given parameters, i.e. the likelihood. We present $\texttt{sbi}$, a PyTorch-based package that implements SBI algorithms based on neural networks. $\texttt{sbi}$ facilitates inference on black-box simulators for practising scientists and engineers by providing a unified interface to state-of-the-art algorithms together with documentation and tutorials.