Scientific Inference With Interpretable Machine Learning: Analyzing Models to Learn About Real-World Phenomena

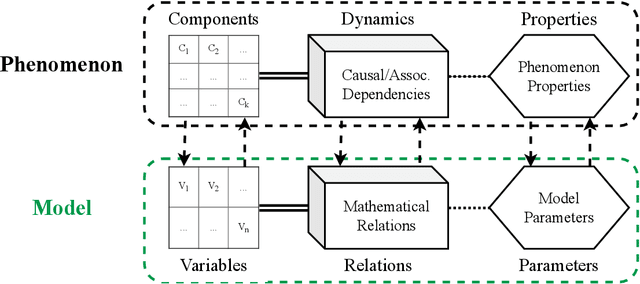
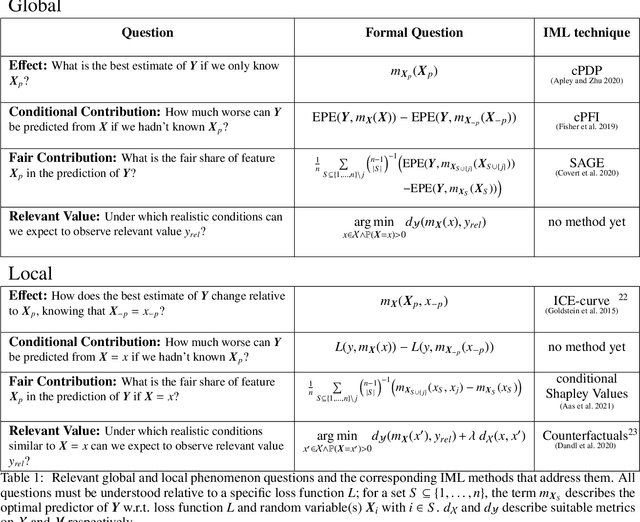
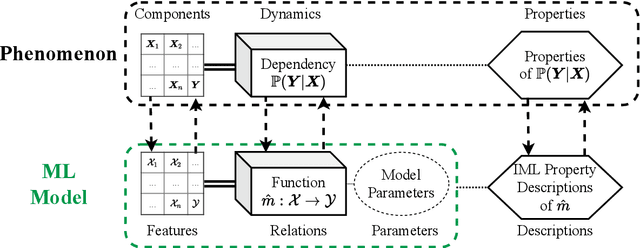
Interpretable machine learning (IML) is concerned with the behavior and the properties of machine learning models. Scientists, however, are only interested in the model as a gateway to understanding the modeled phenomenon. We show how to develop IML methods such that they allow insight into relevant phenomenon properties. We argue that current IML research conflates two goals of model-analysis -- model audit and scientific inference. Thereby, it remains unclear if model interpretations have corresponding phenomenon interpretation. Building on statistical decision theory, we show that ML model analysis allows to describe relevant aspects of the joint data probability distribution. We provide a five-step framework for constructing IML descriptors that can help in addressing scientific questions, including a natural way to quantify epistemic uncertainty. Our phenomenon-centric approach to IML in science clarifies: the opportunities and limitations of IML for inference; that conditional not marginal sampling is required; and, the conditions under which we can trust IML methods.

Marginal Effects for Non-Linear Prediction Functions

Beta coefficients for linear regression models represent the ideal form of an interpretable feature effect. However, for non-linear models and especially generalized linear models, the estimated coefficients cannot be interpreted as a direct feature effect on the predicted outcome. Hence, marginal effects are typically used as approximations for feature effects, either in the shape of derivatives of the prediction function or forward differences in prediction due to a change in a feature value. While marginal effects are commonly used in many scientific fields, they have not yet been adopted as a model-agnostic interpretation method for machine learning models. This may stem from their inflexibility as a univariate feature effect and their inability to deal with the non-linearities found in black box models. We introduce a new class of marginal effects termed forward marginal effects. We argue to abandon derivatives in favor of better-interpretable forward differences. Furthermore, we generalize marginal effects based on forward differences to multivariate changes in feature values. To account for the non-linearity of prediction functions, we introduce a non-linearity measure for marginal effects. We argue against summarizing feature effects of a non-linear prediction function in a single metric such as the average marginal effect. Instead, we propose to partition the feature space to compute conditional average marginal effects on feature subspaces, which serve as conditional feature effect estimates.

Relating the Partial Dependence Plot and Permutation Feature Importance to the Data Generating Process

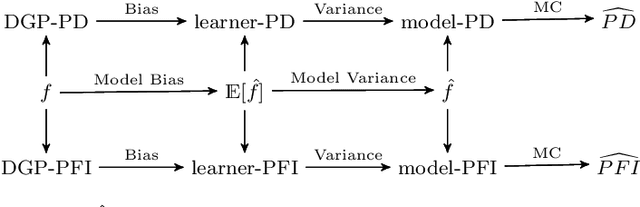
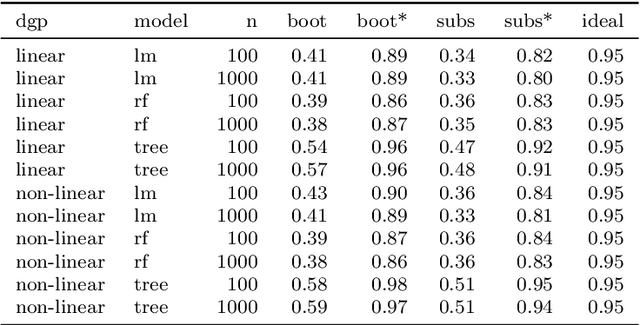
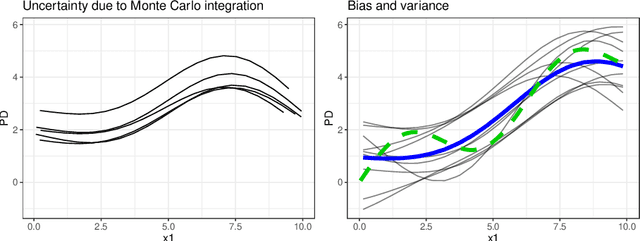
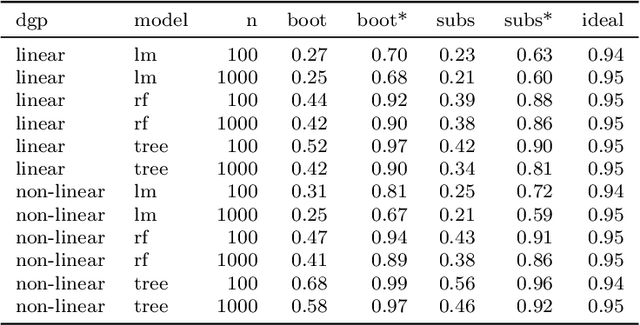
Scientists and practitioners increasingly rely on machine learning to model data and draw conclusions. Compared to statistical modeling approaches, machine learning makes fewer explicit assumptions about data structures, such as linearity. However, their model parameters usually cannot be easily related to the data generating process. To learn about the modeled relationships, partial dependence (PD) plots and permutation feature importance (PFI) are often used as interpretation methods. However, PD and PFI lack a theory that relates them to the data generating process. We formalize PD and PFI as statistical estimators of ground truth estimands rooted in the data generating process. We show that PD and PFI estimates deviate from this ground truth due to statistical biases, model variance and Monte Carlo approximation errors. To account for model variance in PD and PFI estimation, we propose the learner-PD and the learner-PFI based on model refits, and propose corrected variance and confidence interval estimators.

Interpretable Machine Learning -- A Brief History, State-of-the-Art and Challenges

We present a brief history of the field of interpretable machine learning (IML), give an overview of state-of-the-art interpretation methods, and discuss challenges. Research in IML has boomed in recent years. As young as the field is, it has over 200 years old roots in regression modeling and rule-based machine learning, starting in the 1960s. Recently, many new IML methods have been proposed, many of them model-agnostic, but also interpretation techniques specific to deep learning and tree-based ensembles. IML methods either directly analyze model components, study sensitivity to input perturbations, or analyze local or global surrogate approximations of the ML model. The field approaches a state of readiness and stability, with many methods not only proposed in research, but also implemented in open-source software. But many important challenges remain for IML, such as dealing with dependent features, causal interpretation, and uncertainty estimation, which need to be resolved for its successful application to scientific problems. A further challenge is a missing rigorous definition of interpretability, which is accepted by the community. To address the challenges and advance the field, we urge to recall our roots of interpretable, data-driven modeling in statistics and (rule-based) ML, but also to consider other areas such as sensitivity analysis, causal inference, and the social sciences.

Relative Feature Importance

Interpretable Machine Learning (IML) methods are used to gain insight into the relevance of a feature of interest for the performance of a model. Commonly used IML methods differ in whether they consider features of interest in isolation, e.g., Permutation Feature Importance (PFI), or in relation to all remaining feature variables, e.g., Conditional Feature Importance (CFI). As such, the perturbation mechanisms inherent to PFI and CFI represent extreme reference points. We introduce Relative Feature Importance (RFI), a generalization of PFI and CFI that allows for a more nuanced feature importance computation beyond the PFI versus CFI dichotomy. With RFI, the importance of a feature relative to any other subset of features can be assessed, including variables that were not available at training time. We derive general interpretation rules for RFI based on a detailed theoretical analysis of the implications of relative feature relevance, and demonstrate the method's usefulness on simulated examples.

Pitfalls to Avoid when Interpreting Machine Learning Models

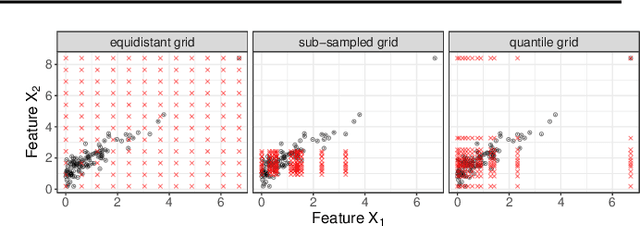
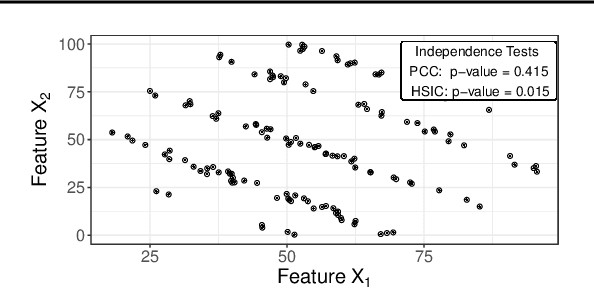
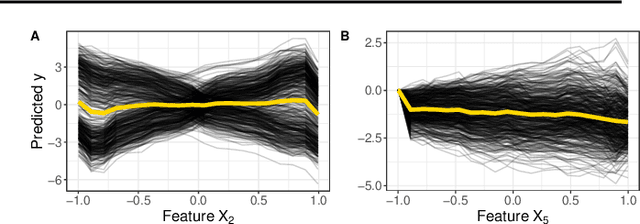
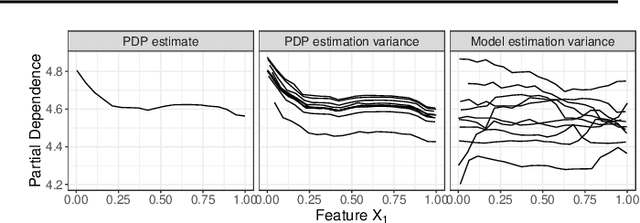
Modern requirements for machine learning (ML) models include both high predictive performance and model interpretability. A growing number of techniques provide model interpretations, but can lead to wrong conclusions if applied incorrectly. We illustrate pitfalls of ML model interpretation such as bad model generalization, dependent features, feature interactions or unjustified causal interpretations. Our paper addresses ML practitioners by raising awareness of pitfalls and pointing out solutions for correct model interpretation, as well as ML researchers by discussing open issues for further research.

Model-agnostic Feature Importance and Effects with Dependent Features -- A Conditional Subgroup Approach

Partial dependence plots and permutation feature importance are popular model-agnostic interpretation methods. Both methods are based on predicting artificially created data points. When features are dependent, both methods extrapolate to feature areas with low data density. The extrapolation can cause misleading interpretations. To overcome extrapolation, we propose conditional variants of partial dependence plots and permutation feature importance. Our approach is based on perturbations in subgroups. The subgroups partition the feature space to make the feature distribution within a group more homogeneous and between the groups more heterogeneous. The interpretable subgroups enable additional local, nuanced interpretations of the feature dependence structure as well as the feature effects and importance values within the subgroups. We also introduce a data fidelity measure that captures the degree of extrapolation when data is transformed with a certain perturbation. In simulations and benchmarks on real data we show that our conditional interpretation methods reduce extrapolation. In an application we show that these methods provide more nuanced and richer explanations.

Multi-Objective Counterfactual Explanations

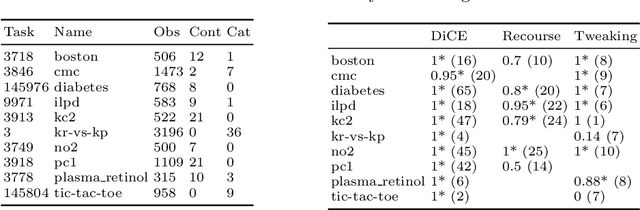
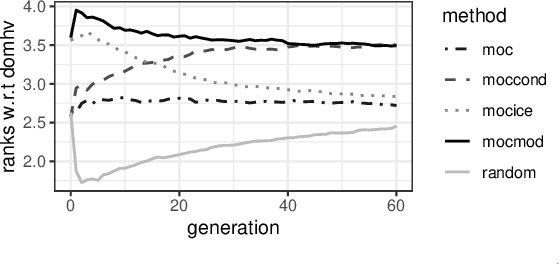
Counterfactual explanations are one of the most popular methods to make predictions of black box machine learning models interpretable by providing explanations in the form of `what-if scenarios'. Current approaches can compute counterfactuals only for certain model classes or feature types, or they generate counterfactuals that are not consistent with the observed data distribution. To overcome these limitations, we propose the Multi-Objective Counterfactuals (MOC) method, which translates the counterfactual search into a multi-objective optimization problem and solves it with a genetic algorithm based on NSGA-II. It returns a diverse set of counterfactuals with different trade-offs between the proposed objectives, enabling either a more detailed post-hoc analysis to facilitate better understanding or more options for actionable user responses to change the predicted outcome. We show the usefulness of MOC in concrete cases and compare our approach with state-of-the-art methods for counterfactual explanations.

Sampling, Intervention, Prediction, Aggregation: A Generalized Framework for Model Agnostic Interpretations

Non-linear machine learning models often trade off a great predictive performance for a lack of interpretability. However, model agnostic interpretation techniques now allow us to estimate the effect and importance of features for any predictive model. Different notations and terminology have complicated their understanding and how they are related. A unified view on these methods has been missing. We present the generalized SIPA (Sampling, Intervention, Prediction, Aggregation) framework of work stages for model agnostic interpretation techniques and demonstrate how several prominent methods for feature effects can be embedded into the proposed framework. We also formally introduce pre-existing marginal effects to describe feature effects for black box models. Furthermore, we extend the framework to feature importance computations by pointing out how variance-based and performance-based importance measures are based on the same work stages. The generalized framework may serve as a guideline to conduct model agnostic interpretations in machine learning.

Quantifying Interpretability of Arbitrary Machine Learning Models Through Functional Decomposition

To obtain interpretable machine learning models, either interpretable models are constructed from the outset - e.g. shallow decision trees, rule lists, or sparse generalized linear models - or post-hoc interpretation methods - e.g. partial dependence or ALE plots - are employed. Both approaches have disadvantages. While the former can restrict the hypothesis space too conservatively, leading to potentially suboptimal solutions, the latter can produce too verbose or misleading results if the resulting model is too complex, especially w.r.t. feature interactions. We propose to make the compromise between predictive power and interpretability explicit by quantifying the complexity / interpretability of machine learning models. Based on functional decomposition, we propose measures of number of features used, interaction strength and main effect complexity. We show that post-hoc interpretation of models that minimize the three measures becomes more reliable and compact. Furthermore, we demonstrate the application of such measures in a multi-objective optimization approach which considers predictive power and interpretability at the same time.