Position Paper: Bridging the Gap Between Machine Learning and Sensitivity Analysis

We argue that interpretations of machine learning (ML) models or the model-building process can bee seen as a form of sensitivity analysis (SA), a general methodology used to explain complex systems in many fields such as environmental modeling, engineering, or economics. We address both researchers and practitioners, calling attention to the benefits of a unified SA-based view of explanations in ML and the necessity to fully credit related work. We bridge the gap between both fields by formally describing how (a) the ML process is a system suitable for SA, (b) how existing ML interpretation methods relate to this perspective, and (c) how other SA techniques could be applied to ML.

fmeffects: An R Package for Forward Marginal Effects

Forward marginal effects (FMEs) have recently been introduced as a versatile and effective model-agnostic interpretation method. They provide comprehensible and actionable model explanations in the form of: If we change $x$ by an amount $h$, what is the change in predicted outcome $\widehat{y}$? We present the R package fmeffects, the first software implementation of FMEs. The relevant theoretical background, package functionality and handling, as well as the software design and options for future extensions are discussed in this paper.

Algorithm-Agnostic Interpretations for Clustering

A clustering outcome for high-dimensional data is typically interpreted via post-processing, involving dimension reduction and subsequent visualization. This destroys the meaning of the data and obfuscates interpretations. We propose algorithm-agnostic interpretation methods to explain clustering outcomes in reduced dimensions while preserving the integrity of the data. The permutation feature importance for clustering represents a general framework based on shuffling feature values and measuring changes in cluster assignments through custom score functions. The individual conditional expectation for clustering indicates observation-wise changes in the cluster assignment due to changes in the data. The partial dependence for clustering evaluates average changes in cluster assignments for the entire feature space. All methods can be used with any clustering algorithm able to reassign instances through soft or hard labels. In contrast to common post-processing methods such as principal component analysis, the introduced methods maintain the original structure of the features.

Marginal Effects for Non-Linear Prediction Functions

Beta coefficients for linear regression models represent the ideal form of an interpretable feature effect. However, for non-linear models and especially generalized linear models, the estimated coefficients cannot be interpreted as a direct feature effect on the predicted outcome. Hence, marginal effects are typically used as approximations for feature effects, either in the shape of derivatives of the prediction function or forward differences in prediction due to a change in a feature value. While marginal effects are commonly used in many scientific fields, they have not yet been adopted as a model-agnostic interpretation method for machine learning models. This may stem from their inflexibility as a univariate feature effect and their inability to deal with the non-linearities found in black box models. We introduce a new class of marginal effects termed forward marginal effects. We argue to abandon derivatives in favor of better-interpretable forward differences. Furthermore, we generalize marginal effects based on forward differences to multivariate changes in feature values. To account for the non-linearity of prediction functions, we introduce a non-linearity measure for marginal effects. We argue against summarizing feature effects of a non-linear prediction function in a single metric such as the average marginal effect. Instead, we propose to partition the feature space to compute conditional average marginal effects on feature subspaces, which serve as conditional feature effect estimates.

Pitfalls to Avoid when Interpreting Machine Learning Models

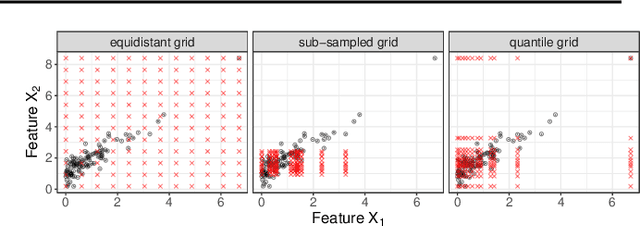
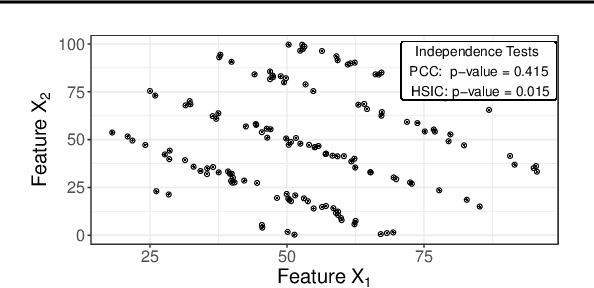
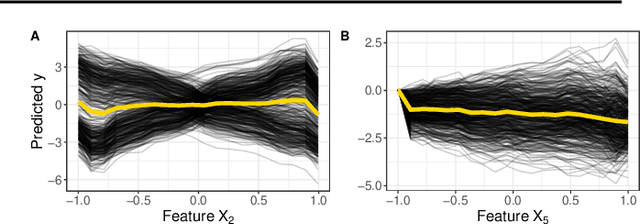
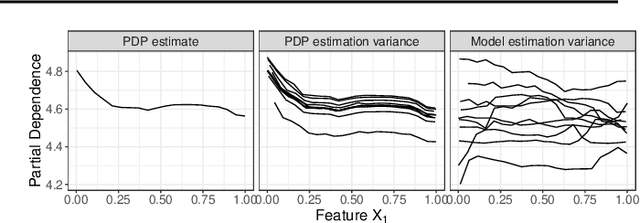
Modern requirements for machine learning (ML) models include both high predictive performance and model interpretability. A growing number of techniques provide model interpretations, but can lead to wrong conclusions if applied incorrectly. We illustrate pitfalls of ML model interpretation such as bad model generalization, dependent features, feature interactions or unjustified causal interpretations. Our paper addresses ML practitioners by raising awareness of pitfalls and pointing out solutions for correct model interpretation, as well as ML researchers by discussing open issues for further research.

Sampling, Intervention, Prediction, Aggregation: A Generalized Framework for Model Agnostic Interpretations

Non-linear machine learning models often trade off a great predictive performance for a lack of interpretability. However, model agnostic interpretation techniques now allow us to estimate the effect and importance of features for any predictive model. Different notations and terminology have complicated their understanding and how they are related. A unified view on these methods has been missing. We present the generalized SIPA (Sampling, Intervention, Prediction, Aggregation) framework of work stages for model agnostic interpretation techniques and demonstrate how several prominent methods for feature effects can be embedded into the proposed framework. We also formally introduce pre-existing marginal effects to describe feature effects for black box models. Furthermore, we extend the framework to feature importance computations by pointing out how variance-based and performance-based importance measures are based on the same work stages. The generalized framework may serve as a guideline to conduct model agnostic interpretations in machine learning.