Disentangling Interactions and Dependencies in Feature Attribution

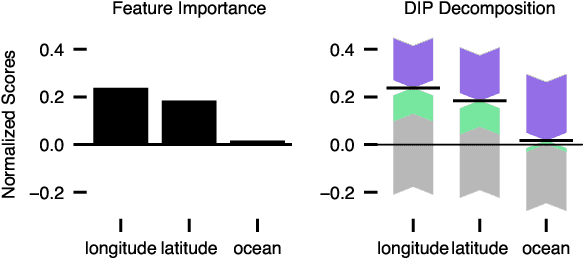
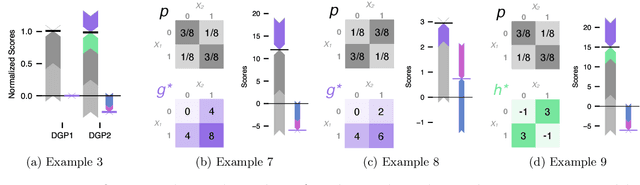
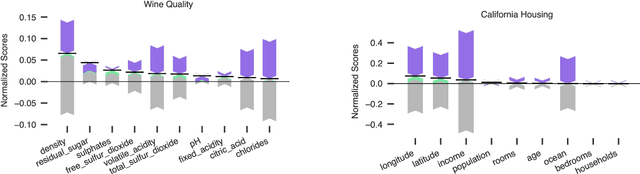
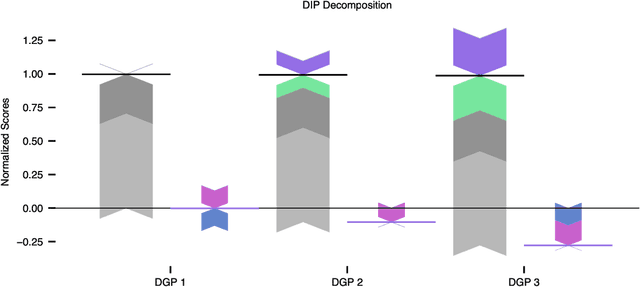
In explainable machine learning, global feature importance methods try to determine how much each individual feature contributes to predicting the target variable, resulting in one importance score for each feature. But often, predicting the target variable requires interactions between several features (such as in the XOR function), and features might have complex statistical dependencies that allow to partially replace one feature with another one. In commonly used feature importance scores these cooperative effects are conflated with the features' individual contributions, making them prone to misinterpretations. In this work, we derive DIP, a new mathematical decomposition of individual feature importance scores that disentangles three components: the standalone contribution and the contributions stemming from interactions and dependencies. We prove that the DIP decomposition is unique and show how it can be estimated in practice. Based on these results, we propose a new visualization of feature importance scores that clearly illustrates the different contributions.

A Guide to Feature Importance Methods for Scientific Inference

While machine learning (ML) models are increasingly used due to their high predictive power, their use in understanding the data-generating process (DGP) is limited. Understanding the DGP requires insights into feature-target associations, which many ML models cannot directly provide, due to their opaque internal mechanisms. Feature importance (FI) methods provide useful insights into the DGP under certain conditions. Since the results of different FI methods have different interpretations, selecting the correct FI method for a concrete use case is crucial and still requires expert knowledge. This paper serves as a comprehensive guide to help understand the different interpretations of FI methods. Through an extensive review of FI methods and providing new proofs regarding their interpretation, we facilitate a thorough understanding of these methods and formulate concrete recommendations for scientific inference. We conclude by discussing options for FI uncertainty estimation and point to directions for future research aiming at full statistical inference from black-box ML models.

CountARFactuals -- Generating plausible model-agnostic counterfactual explanations with adversarial random forests

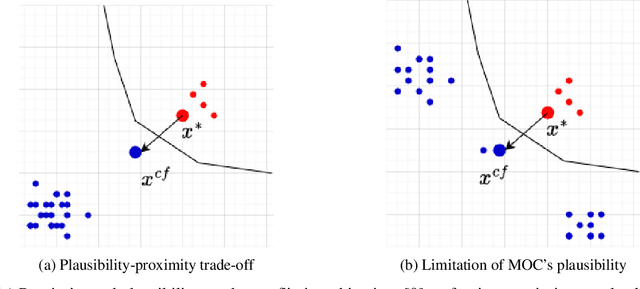
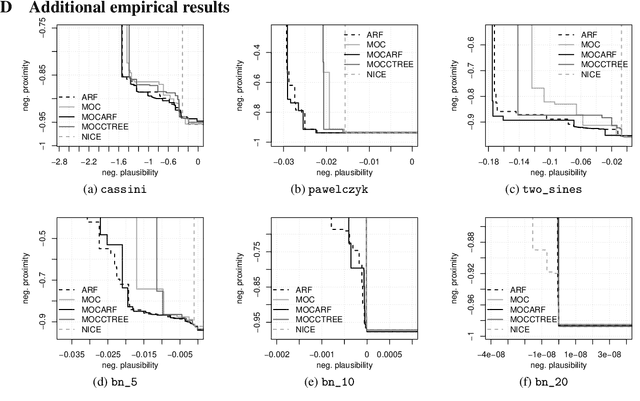
Counterfactual explanations elucidate algorithmic decisions by pointing to scenarios that would have led to an alternative, desired outcome. Giving insight into the model's behavior, they hint users towards possible actions and give grounds for contesting decisions. As a crucial factor in achieving these goals, counterfactuals must be plausible, i.e., describing realistic alternative scenarios within the data manifold. This paper leverages a recently developed generative modeling technique -- adversarial random forests (ARFs) -- to efficiently generate plausible counterfactuals in a model-agnostic way. ARFs can serve as a plausibility measure or directly generate counterfactual explanations. Our ARF-based approach surpasses the limitations of existing methods that aim to generate plausible counterfactual explanations: It is easy to train and computationally highly efficient, handles continuous and categorical data naturally, and allows integrating additional desiderata such as sparsity in a straightforward manner.

Dear XAI Community, We Need to Talk! Fundamental Misconceptions in Current XAI Research

Despite progress in the field, significant parts of current XAI research are still not on solid conceptual, ethical, or methodological grounds. Unfortunately, these unfounded parts are not on the decline but continue to grow. Many explanation techniques are still proposed without clarifying their purpose. Instead, they are advertised with ever more fancy-looking heatmaps or only seemingly relevant benchmarks. Moreover, explanation techniques are motivated with questionable goals, such as building trust, or rely on strong assumptions about the 'concepts' that deep learning algorithms learn. In this paper, we highlight and discuss these and other misconceptions in current XAI research. We also suggest steps to make XAI a more substantive area of research.

Efficient SAGE Estimation via Causal Structure Learning

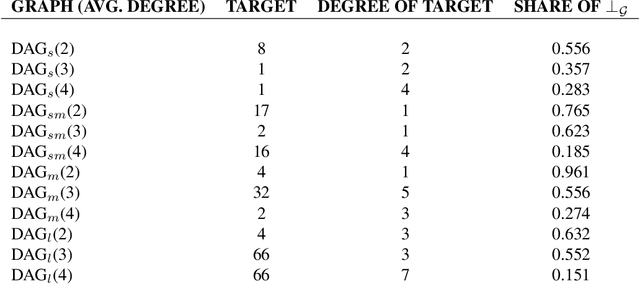
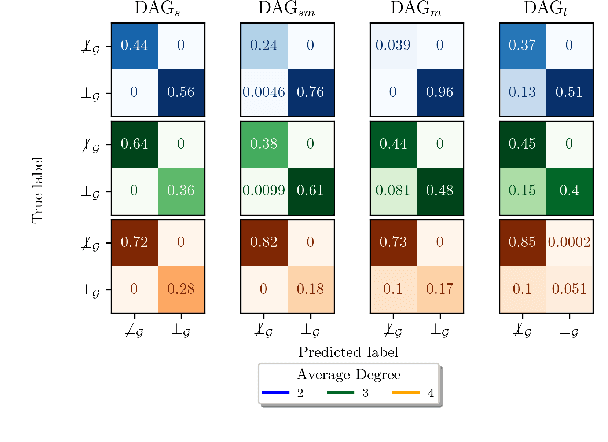
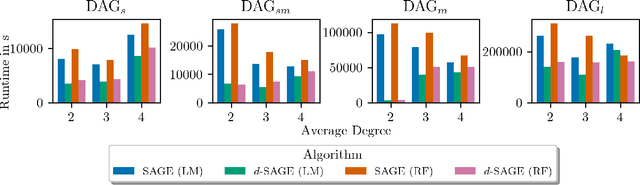
The Shapley Additive Global Importance (SAGE) value is a theoretically appealing interpretability method that fairly attributes global importance to a model's features. However, its exact calculation requires the computation of the feature's surplus performance contributions over an exponential number of feature sets. This is computationally expensive, particularly because estimating the surplus contributions requires sampling from conditional distributions. Thus, SAGE approximation algorithms only take a fraction of the feature sets into account. We propose $d$-SAGE, a method that accelerates SAGE approximation. $d$-SAGE is motivated by the observation that conditional independencies (CIs) between a feature and the model target imply zero surplus contributions, such that their computation can be skipped. To identify CIs, we leverage causal structure learning (CSL) to infer a graph that encodes (conditional) independencies in the data as $d$-separations. This is computationally more efficient because the expense of the one-time graph inference and the $d$-separation queries is negligible compared to the expense of surplus contribution evaluations. Empirically we demonstrate that $d$-SAGE enables the efficient and accurate estimation of SAGE values.

Improvement-Focused Causal Recourse (ICR)

Algorithmic recourse recommendations, such as Karimi et al.'s (2021) causal recourse (CR), inform stakeholders of how to act to revert unfavourable decisions. However, some actions lead to acceptance (i.e., revert the model's decision) but do not lead to improvement (i.e., may not revert the underlying real-world state). To recommend such actions is to recommend fooling the predictor. We introduce a novel method, Improvement-Focused Causal Recourse (ICR), which involves a conceptual shift: Firstly, we require ICR recommendations to guide towards improvement. Secondly, we do not tailor the recommendations to be accepted by a specific predictor. Instead, we leverage causal knowledge to design decision systems that predict accurately pre- and post-recourse. As a result, improvement guarantees translate into acceptance guarantees. We demonstrate that given correct causal knowledge, ICR, in contrast to existing approaches, guides towards both acceptance and improvement.

Scientific Inference With Interpretable Machine Learning: Analyzing Models to Learn About Real-World Phenomena

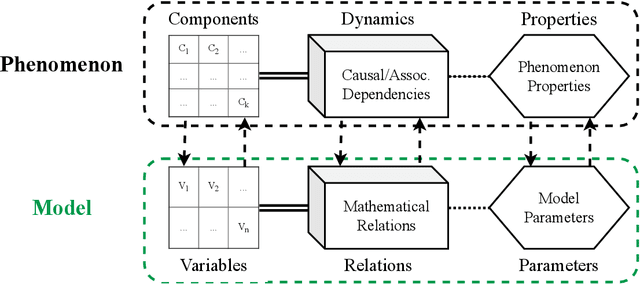
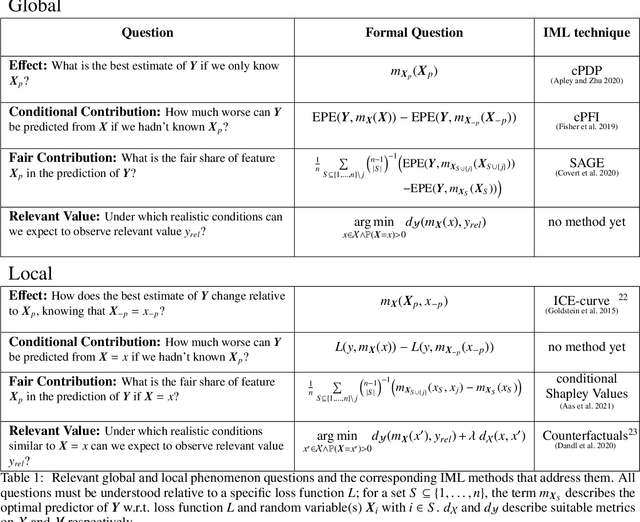
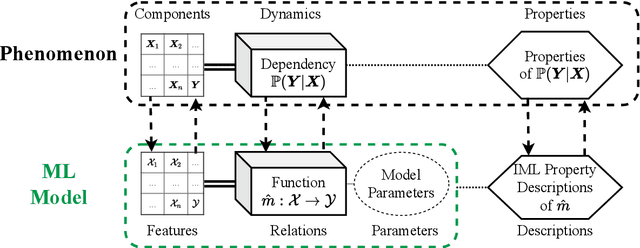
Interpretable machine learning (IML) is concerned with the behavior and the properties of machine learning models. Scientists, however, are only interested in the model as a gateway to understanding the modeled phenomenon. We show how to develop IML methods such that they allow insight into relevant phenomenon properties. We argue that current IML research conflates two goals of model-analysis -- model audit and scientific inference. Thereby, it remains unclear if model interpretations have corresponding phenomenon interpretation. Building on statistical decision theory, we show that ML model analysis allows to describe relevant aspects of the joint data probability distribution. We provide a five-step framework for constructing IML descriptors that can help in addressing scientific questions, including a natural way to quantify epistemic uncertainty. Our phenomenon-centric approach to IML in science clarifies: the opportunities and limitations of IML for inference; that conditional not marginal sampling is required; and, the conditions under which we can trust IML methods.

Relating the Partial Dependence Plot and Permutation Feature Importance to the Data Generating Process

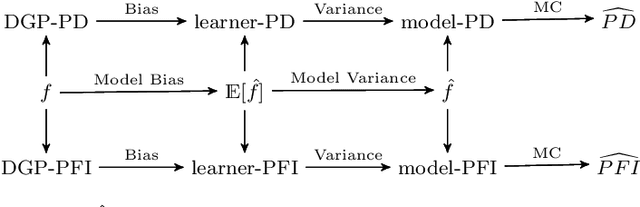
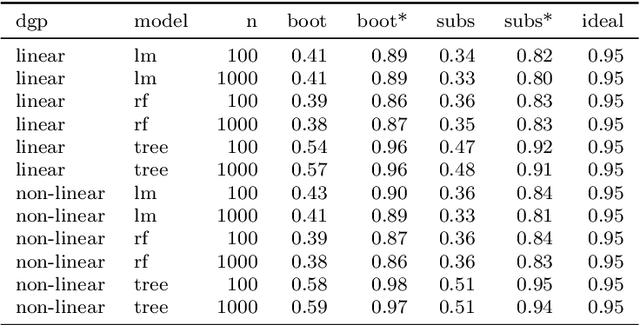
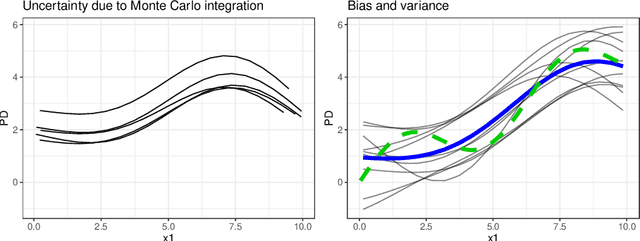
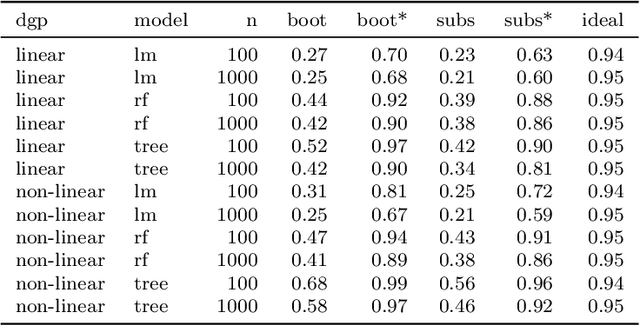
Scientists and practitioners increasingly rely on machine learning to model data and draw conclusions. Compared to statistical modeling approaches, machine learning makes fewer explicit assumptions about data structures, such as linearity. However, their model parameters usually cannot be easily related to the data generating process. To learn about the modeled relationships, partial dependence (PD) plots and permutation feature importance (PFI) are often used as interpretation methods. However, PD and PFI lack a theory that relates them to the data generating process. We formalize PD and PFI as statistical estimators of ground truth estimands rooted in the data generating process. We show that PD and PFI estimates deviate from this ground truth due to statistical biases, model variance and Monte Carlo approximation errors. To account for model variance in PD and PFI estimation, we propose the learner-PD and the learner-PFI based on model refits, and propose corrected variance and confidence interval estimators.

A Causal Perspective on Meaningful and Robust Algorithmic Recourse

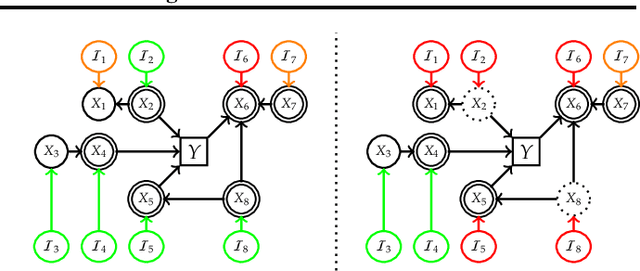
Algorithmic recourse explanations inform stakeholders on how to act to revert unfavorable predictions. However, in general ML models do not predict well in interventional distributions. Thus, an action that changes the prediction in the desired way may not lead to an improvement of the underlying target. Such recourse is neither meaningful nor robust to model refits. Extending the work of Karimi et al. (2021), we propose meaningful algorithmic recourse (MAR) that only recommends actions that improve both prediction and target. We justify this selection constraint by highlighting the differences between model audit and meaningful, actionable recourse explanations. Additionally, we introduce a relaxation of MAR called effective algorithmic recourse (EAR), which, under certain assumptions, yields meaningful recourse by only allowing interventions on causes of the target.

Decomposition of Global Feature Importance into Direct and Associative Components (DEDACT)

Global model-agnostic feature importance measures either quantify whether features are directly used for a model's predictions (direct importance) or whether they contain prediction-relevant information (associative importance). Direct importance provides causal insight into the model's mechanism, yet it fails to expose the leakage of information from associated but not directly used variables. In contrast, associative importance exposes information leakage but does not provide causal insight into the model's mechanism. We introduce DEDACT - a framework to decompose well-established direct and associative importance measures into their respective associative and direct components. DEDACT provides insight into both the sources of prediction-relevant information in the data and the direct and indirect feature pathways by which the information enters the model. We demonstrate the method's usefulness on simulated examples.