Conditional Feature Importance with Generative Modeling Using Adversarial Random Forests

This paper proposes a method for measuring conditional feature importance via generative modeling. In explainable artificial intelligence (XAI), conditional feature importance assesses the impact of a feature on a prediction model's performance given the information of other features. Model-agnostic post hoc methods to do so typically evaluate changes in the predictive performance under on-manifold feature value manipulations. Such procedures require creating feature values that respect conditional feature distributions, which can be challenging in practice. Recent advancements in generative modeling can facilitate this. For tabular data, which may consist of both categorical and continuous features, the adversarial random forest (ARF) stands out as a generative model that can generate on-manifold data points without requiring intensive tuning efforts or computational resources, making it a promising candidate model for subroutines in XAI methods. This paper proposes cARFi (conditional ARF feature importance), a method for measuring conditional feature importance through feature values sampled from ARF-estimated conditional distributions. cARFi requires only little tuning to yield robust importance scores that can flexibly adapt for conditional or marginal notions of feature importance, including straightforward extensions to condition on feature subsets and allows for inferring the significance of feature importances through statistical tests.

CountARFactuals -- Generating plausible model-agnostic counterfactual explanations with adversarial random forests

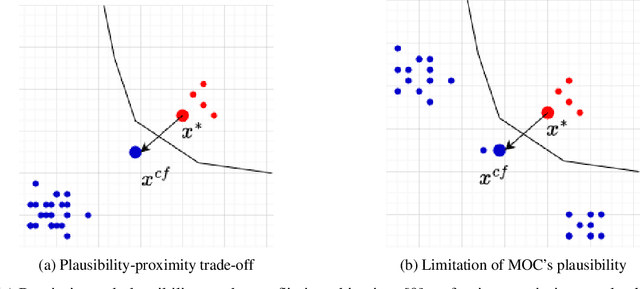
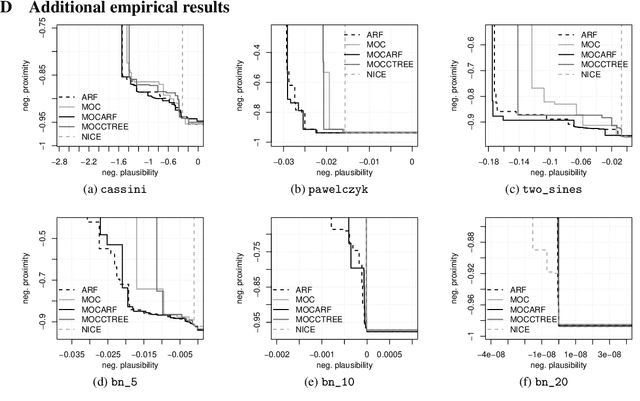
Counterfactual explanations elucidate algorithmic decisions by pointing to scenarios that would have led to an alternative, desired outcome. Giving insight into the model's behavior, they hint users towards possible actions and give grounds for contesting decisions. As a crucial factor in achieving these goals, counterfactuals must be plausible, i.e., describing realistic alternative scenarios within the data manifold. This paper leverages a recently developed generative modeling technique -- adversarial random forests (ARFs) -- to efficiently generate plausible counterfactuals in a model-agnostic way. ARFs can serve as a plausibility measure or directly generate counterfactual explanations. Our ARF-based approach surpasses the limitations of existing methods that aim to generate plausible counterfactual explanations: It is easy to train and computationally highly efficient, handles continuous and categorical data naturally, and allows integrating additional desiderata such as sparsity in a straightforward manner.

arfpy: A python package for density estimation and generative modeling with adversarial random forests

This paper introduces $\textit{arfpy}$, a python implementation of Adversarial Random Forests (ARF) (Watson et al., 2023), which is a lightweight procedure for synthesizing new data that resembles some given data. The software $\textit{arfpy}$ equips practitioners with straightforward functionalities for both density estimation and generative modeling. The method is particularly useful for tabular data and its competitive performance is demonstrated in previous literature. As a major advantage over the mostly deep learning based alternatives, $\textit{arfpy}$ combines the method's reduced requirements in tuning efforts and computational resources with a user-friendly python interface. This supplies audiences across scientific fields with software to generate data effortlessly.

Conditional Feature Importance for Mixed Data

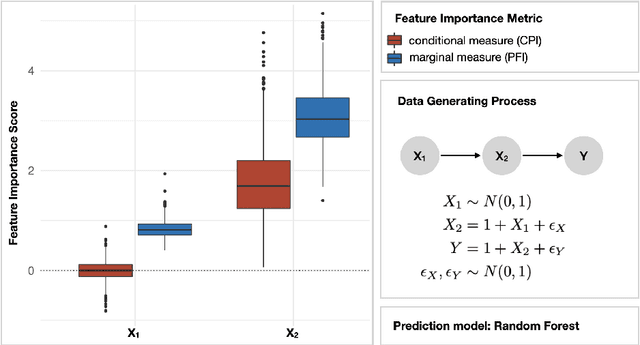
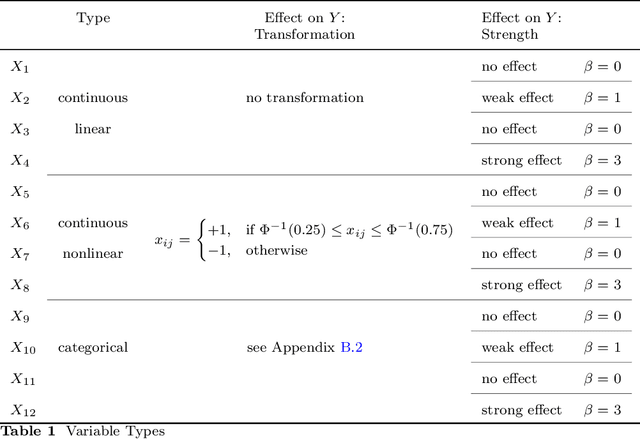
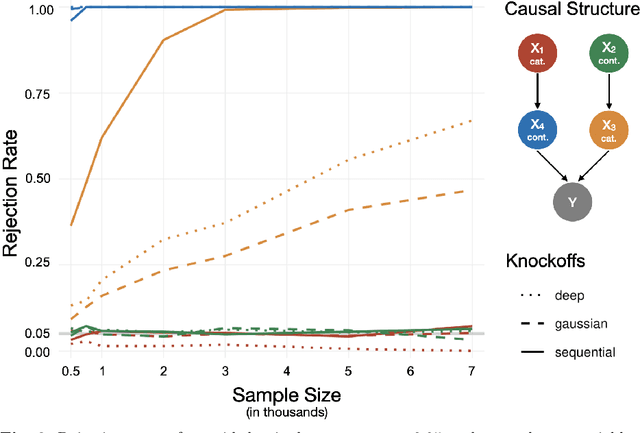
Despite the popularity of feature importance measures in interpretable machine learning, the statistical adequacy of these methods is rarely discussed. From a statistical perspective, a major distinction is between analyzing a variable's importance before and after adjusting for covariates - i.e., between marginal and conditional measures. Our work draws attention to this rarely acknowledged, yet crucial distinction and showcases its implications. Further, we reveal that for testing conditional feature importance (CFI), only few methods are available and practitioners have hitherto been severely restricted in method application due to mismatching data requirements. Most real-world data exhibits complex feature dependencies and incorporates both continuous and categorical data (mixed data). Both properties are oftentimes neglected by CFI measures. To fill this gap, we propose to combine the conditional predictive impact (CPI) framework (arXiv:1901.09917) with sequential knockoff sampling (arXiv:2010.14026). The CPI enables CFI measurement that controls for any feature dependencies by sampling valid knockoffs - hence, generating synthetic data with similar statistical properties - for the data to be analyzed. Sequential knockoffs were deliberately designed to handle mixed data and thus allow us to extend the CPI approach to such datasets. We demonstrate through numerous simulations and a real-world example that our proposed workflow controls type I error, achieves high power and is in line with results given by other CFI measures, whereas marginal feature importance metrics result in misleading interpretations. Our findings highlight the necessity of developing statistically adequate, specialized methods for mixed data.

Smooth densities and generative modeling with unsupervised random forests

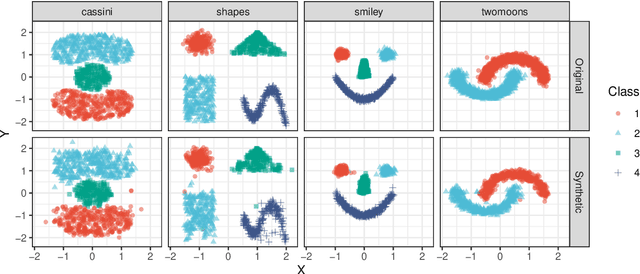
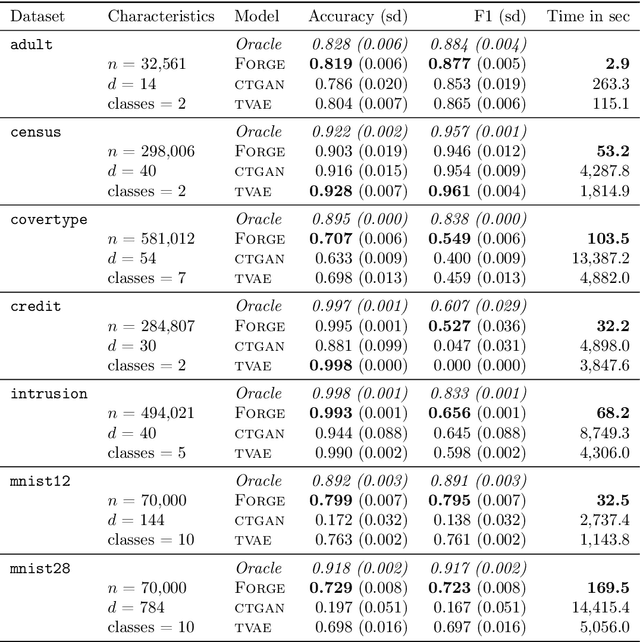
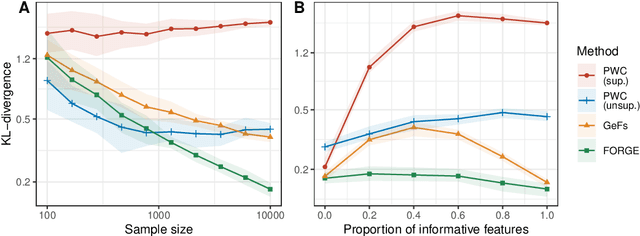
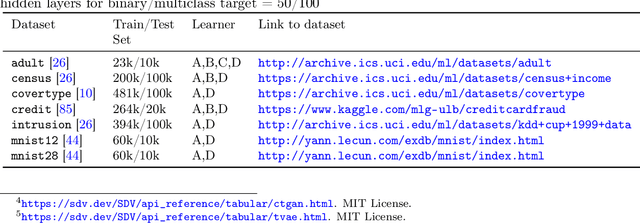
Density estimation is a fundamental problem in statistics, and any attempt to do so in high dimensions typically requires strong assumptions or complex deep learning architectures. An important application for density estimators is synthetic data generation, an area currently dominated by neural networks that often demand enormous training datasets and extensive tuning. We propose a new method based on unsupervised random forests for estimating smooth densities in arbitrary dimensions without parametric constraints, as well as generating realistic synthetic data. We prove the consistency of our approach and demonstrate its advantages over existing tree-based density estimators, which generally rely on ill-chosen split criteria and do not scale well with data dimensionality. Experiments illustrate that our algorithm compares favorably to state-of-the-art deep learning generative models, achieving superior performance in a range of benchmark trials while executing about two orders of magnitude faster on average. Our method is implemented in easy-to-use $\texttt{R}$ and Python packages.