Gradient-based Explanations for Deep Learning Survival Models

Deep learning survival models often outperform classical methods in time-to-event predictions, particularly in personalized medicine, but their "black box" nature hinders broader adoption. We propose a framework for gradient-based explanation methods tailored to survival neural networks, extending their use beyond regression and classification. We analyze the implications of their theoretical assumptions for time-dependent explanations in the survival setting and propose effective visualizations incorporating the temporal dimension. Experiments on synthetic data show that gradient-based methods capture the magnitude and direction of local and global feature effects, including time dependencies. We introduce GradSHAP(t), a gradient-based counterpart to SurvSHAP(t), which outperforms SurvSHAP(t) and SurvLIME in a computational speed vs. accuracy trade-off. Finally, we apply these methods to medical data with multi-modal inputs, revealing relevant tabular features and visual patterns, as well as their temporal dynamics.

Conditional Feature Importance with Generative Modeling Using Adversarial Random Forests

This paper proposes a method for measuring conditional feature importance via generative modeling. In explainable artificial intelligence (XAI), conditional feature importance assesses the impact of a feature on a prediction model's performance given the information of other features. Model-agnostic post hoc methods to do so typically evaluate changes in the predictive performance under on-manifold feature value manipulations. Such procedures require creating feature values that respect conditional feature distributions, which can be challenging in practice. Recent advancements in generative modeling can facilitate this. For tabular data, which may consist of both categorical and continuous features, the adversarial random forest (ARF) stands out as a generative model that can generate on-manifold data points without requiring intensive tuning efforts or computational resources, making it a promising candidate model for subroutines in XAI methods. This paper proposes cARFi (conditional ARF feature importance), a method for measuring conditional feature importance through feature values sampled from ARF-estimated conditional distributions. cARFi requires only little tuning to yield robust importance scores that can flexibly adapt for conditional or marginal notions of feature importance, including straightforward extensions to condition on feature subsets and allows for inferring the significance of feature importances through statistical tests.

Toward Understanding the Disagreement Problem in Neural Network Feature Attribution

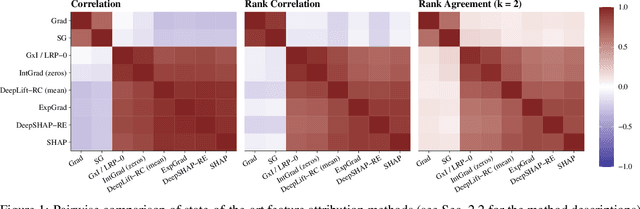
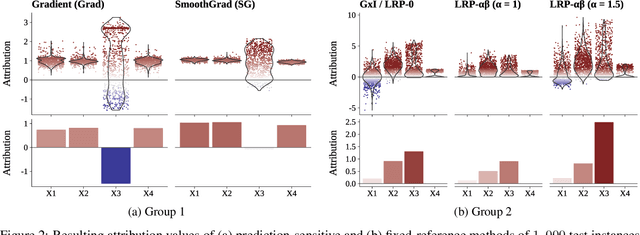
In recent years, neural networks have demonstrated their remarkable ability to discern intricate patterns and relationships from raw data. However, understanding the inner workings of these black box models remains challenging, yet crucial for high-stake decisions. Among the prominent approaches for explaining these black boxes are feature attribution methods, which assign relevance or contribution scores to each input variable for a model prediction. Despite the plethora of proposed techniques, ranging from gradient-based to backpropagation-based methods, a significant debate persists about which method to use. Various evaluation metrics have been proposed to assess the trustworthiness or robustness of their results. However, current research highlights disagreement among state-of-the-art methods in their explanations. Our work addresses this confusion by investigating the explanations' fundamental and distributional behavior. Additionally, through a comprehensive simulation study, we illustrate the impact of common scaling and encoding techniques on the explanation quality, assess their efficacy across different effect sizes, and demonstrate the origin of inconsistency in rank-based evaluation metrics.

Interpreting Deep Neural Networks with the Package innsight

The R package innsight offers a general toolbox for revealing variable-wise interpretations of deep neural networks' predictions with so-called feature attribution methods. Aside from the unified and user-friendly framework, the package stands out in three ways: It is generally the first R package implementing feature attribution methods for neural networks. Secondly, it operates independently of the deep learning library allowing the interpretation of models from any R package, including keras, torch, neuralnet, and even custom models. Despite its flexibility, innsight benefits internally from the torch package's fast and efficient array calculations, which builds on LibTorch $-$ PyTorch's C++ backend $-$ without a Python dependency. Finally, it offers a variety of visualization tools for tabular, signal, image data or a combination of these. Additionally, the plots can be rendered interactively using the plotly package.

Generalization of the Change of Variables Formula with Applications to Residual Flows

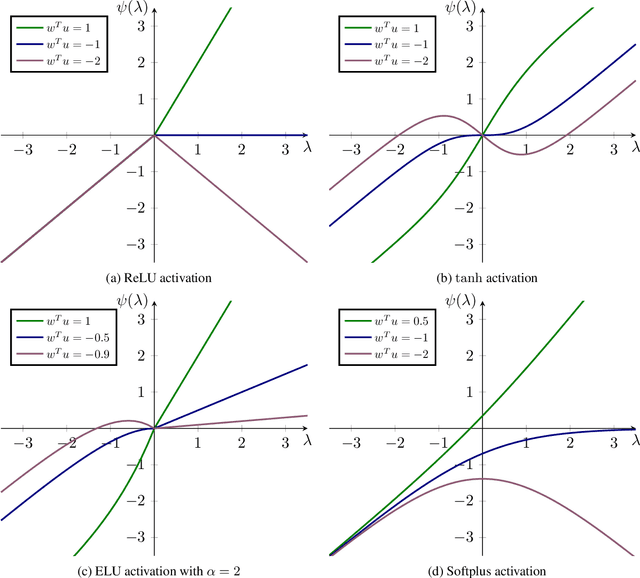
Normalizing flows leverage the Change of Variables Formula (CVF) to define flexible density models. Yet, the requirement of smooth transformations (diffeomorphisms) in the CVF poses a significant challenge in the construction of these models. To enlarge the design space of flows, we introduce $\mathcal{L}$-diffeomorphisms as generalized transformations which may violate these requirements on zero Lebesgue-measure sets. This relaxation allows e.g. the use of non-smooth activation functions such as ReLU. Finally, we apply the obtained results to planar, radial, and contractive residual flows.