Generalization of the Change of Variables Formula with Applications to Residual Flows
Paper and Code
Jul 09, 2021

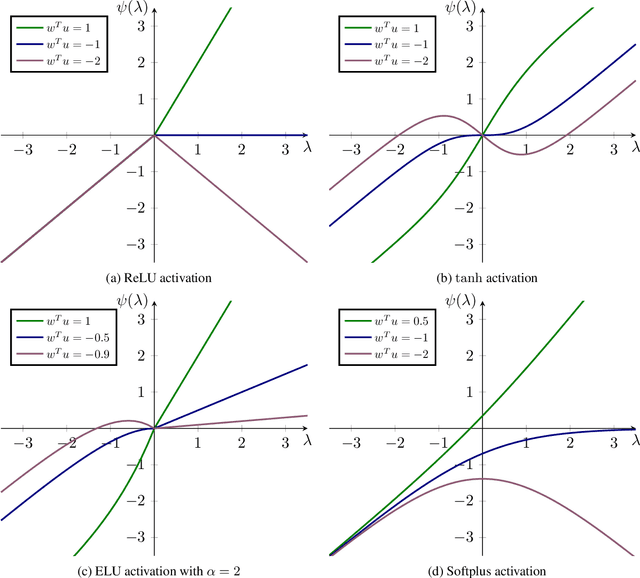
Normalizing flows leverage the Change of Variables Formula (CVF) to define flexible density models. Yet, the requirement of smooth transformations (diffeomorphisms) in the CVF poses a significant challenge in the construction of these models. To enlarge the design space of flows, we introduce $\mathcal{L}$-diffeomorphisms as generalized transformations which may violate these requirements on zero Lebesgue-measure sets. This relaxation allows e.g. the use of non-smooth activation functions such as ReLU. Finally, we apply the obtained results to planar, radial, and contractive residual flows.
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge