Smooth Deep Saliency

In this work, we investigate methods to reduce the noise in deep saliency maps coming from convolutional downsampling, with the purpose of explaining how a deep learning model detects tumors in scanned histological tissue samples. Those methods make the investigated models more interpretable for gradient-based saliency maps, computed in hidden layers. We test our approach on different models trained for image classification on ImageNet1K, and models trained for tumor detection on Camelyon16 and in-house real-world digital pathology scans of stained tissue samples. Our results show that the checkerboard noise in the gradient gets reduced, resulting in smoother and therefore easier to interpret saliency maps.

Is Deep Image Prior in Need of a Good Education?

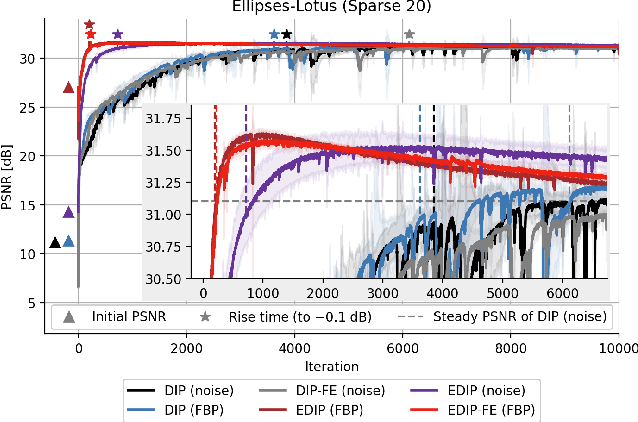
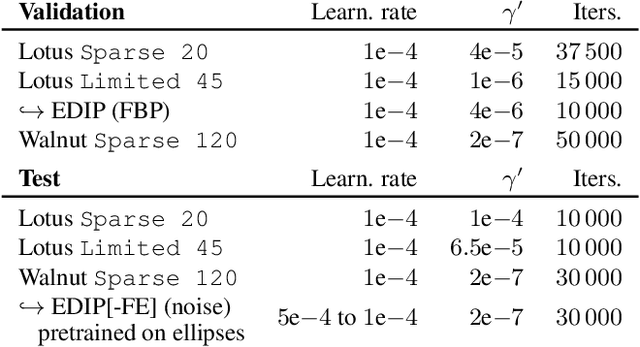
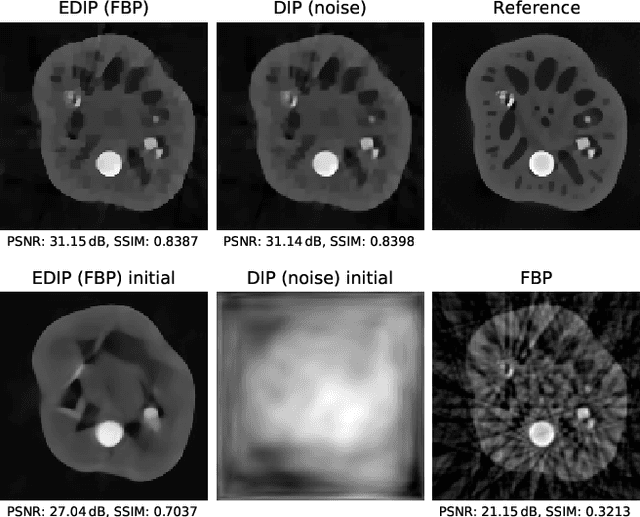
Deep image prior was recently introduced as an effective prior for image reconstruction. It represents the image to be recovered as the output of a deep convolutional neural network, and learns the network's parameters such that the output fits the corrupted observation. Despite its impressive reconstructive properties, the approach is slow when compared to learned or traditional reconstruction techniques. Our work develops a two-stage learning paradigm to address the computational challenge: (i) we perform a supervised pretraining of the network on a synthetic dataset; (ii) we fine-tune the network's parameters to adapt to the target reconstruction. We showcase that pretraining considerably speeds up the subsequent reconstruction from real-measured micro computed tomography data of biological specimens. The code and additional experimental materials are available at https://educateddip.github.io/docs.educated_deep_image_prior/.

Generalization of the Change of Variables Formula with Applications to Residual Flows

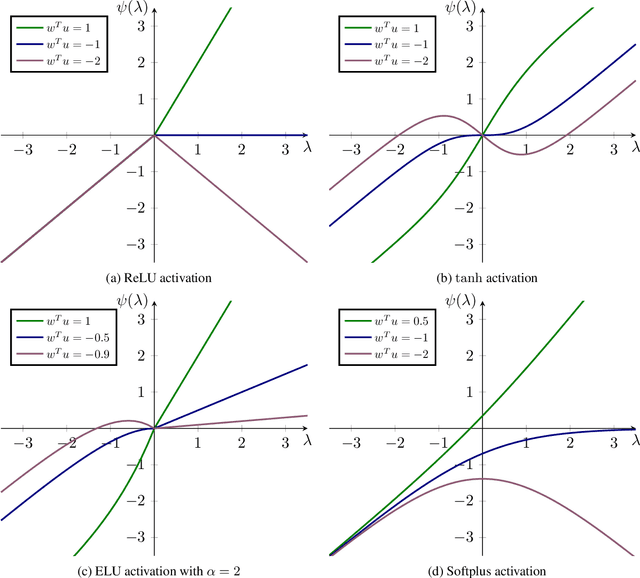
Normalizing flows leverage the Change of Variables Formula (CVF) to define flexible density models. Yet, the requirement of smooth transformations (diffeomorphisms) in the CVF poses a significant challenge in the construction of these models. To enlarge the design space of flows, we introduce $\mathcal{L}$-diffeomorphisms as generalized transformations which may violate these requirements on zero Lebesgue-measure sets. This relaxation allows e.g. the use of non-smooth activation functions such as ReLU. Finally, we apply the obtained results to planar, radial, and contractive residual flows.

Deeply supervised UNet for semantic segmentation to assist dermatopathological assessment of Basal Cell Carcinoma (BCC)

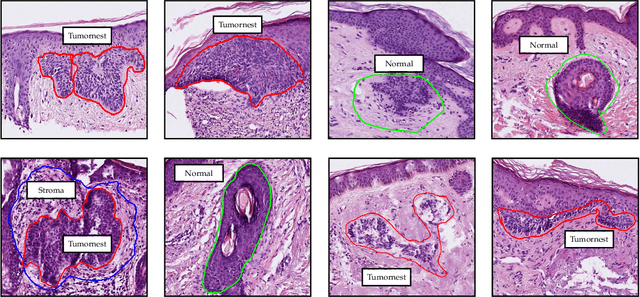
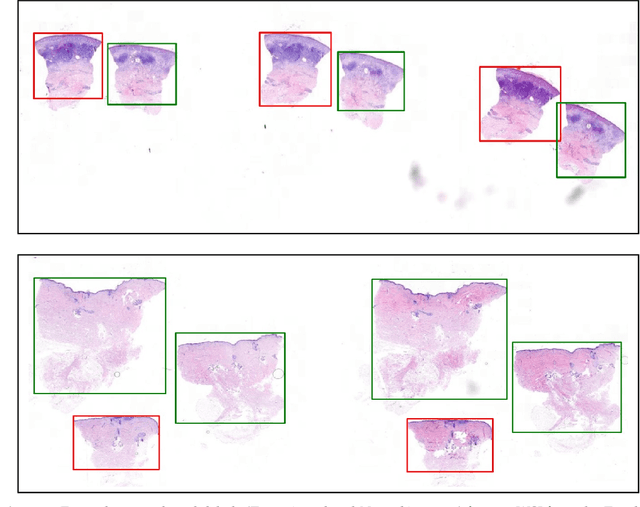
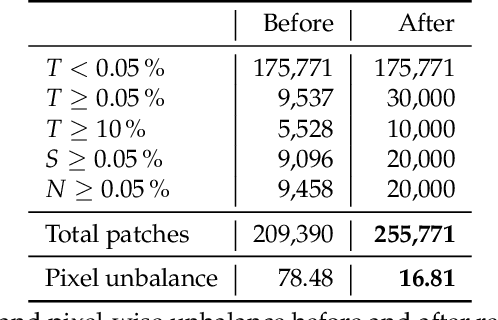
Accurate and fast assessment of resection margins is an essential part of a dermatopathologist's clinical routine. In this work, we successfully develop a deep learning method to assist the pathologists by marking critical regions that have a high probability of exhibiting pathological features in Whole Slide Images (WSI). We focus on detecting Basal Cell Carcinoma (BCC) through semantic segmentation using several models based on the UNet architecture. The study includes 650 WSI with 3443 tissue sections in total. Two clinical dermatopathologists annotated the data, marking tumor tissues' exact location on 100 WSI. The rest of the data, with ground-truth section-wise labels, is used to further validate and test the models. We analyze two different encoders for the first part of the UNet network and two additional training strategies: a) deep supervision, b) linear combination of decoder outputs, and obtain some interpretations about what the network's decoder does in each case. The best model achieves over 96%, accuracy, sensitivity, and specificity on the test set.

The LoDoPaB-CT Dataset: A Benchmark Dataset for Low-Dose CT Reconstruction Methods

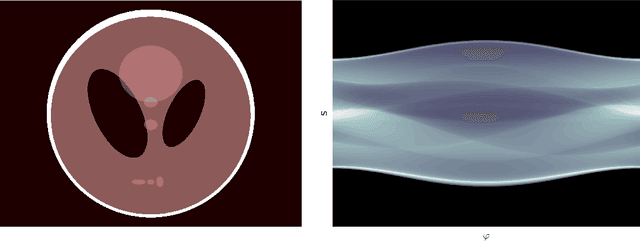
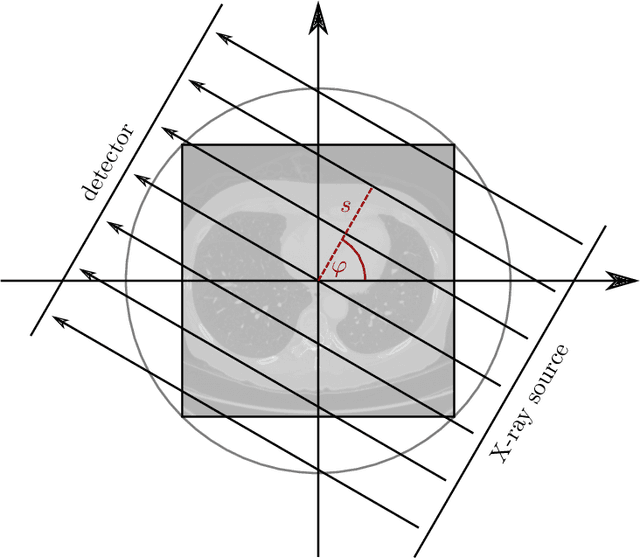
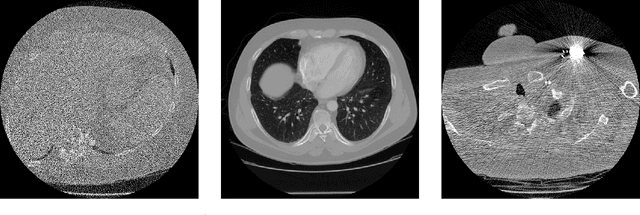
Deep Learning approaches for solving Inverse Problems in imaging have become very effective and are demonstrated to be quite competitive in the field. Comparing these approaches is a challenging task since they highly rely on the data and the setup that is used for training. We provide a public dataset of computed tomography images and simulated low-dose measurements suitable for training this kind of methods. With the LoDoPaB-CT Dataset we aim to create a benchmark that allows for a fair comparison. It contains over 40,000 scan slices from around 800 patients selected from the LIDC/IDRI Database. In this paper we describe how we processed the original slices and how we simulated the measurements. We also include first baseline results.

Analysis of Invariance and Robustness via Invertibility of ReLU-Networks

Studying the invertibility of deep neural networks (DNNs) provides a principled approach to better understand the behavior of these powerful models. Despite being a promising diagnostic tool, a consistent theory on their invertibility is still lacking. We derive a theoretically motivated approach to explore the preimages of ReLU-layers and mechanisms affecting the stability of the inverse. Using the developed theory, we numerically show how this approach uncovers characteristic properties of the network.