Convergence of Stochastic Gradient Methods for Wide Two-Layer Physics-Informed Neural Networks

Physics informed neural networks (PINNs) represent a very popular class of neural solvers for partial differential equations. In practice, one often employs stochastic gradient descent type algorithms to train the neural network. Therefore, the convergence guarantee of stochastic gradient descent is of fundamental importance. In this work, we establish the linear convergence of stochastic gradient descent / flow in training over-parameterized two layer PINNs for a general class of activation functions in the sense of high probability. These results extend the existing result [18] in which gradient descent was analyzed. The challenge of the analysis lies in handling the dynamic randomness introduced by stochastic optimization methods. The key of the analysis lies in ensuring the positive definiteness of suitable Gram matrices during the training. The analysis sheds insight into the dynamics of the optimization process, and provides guarantees on the neural networks trained by stochastic algorithms.

Deep Learning Based Reconstruction Methods for Electrical Impedance Tomography

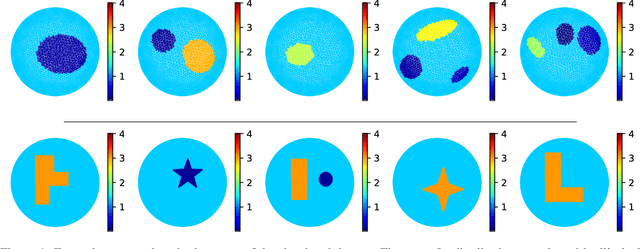
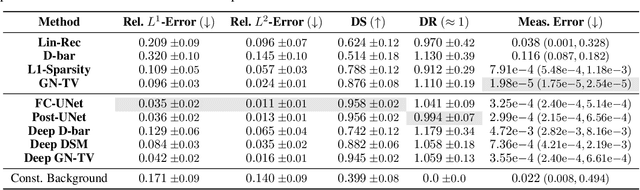
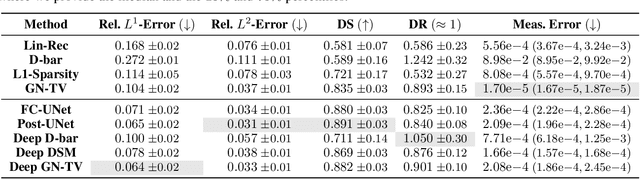
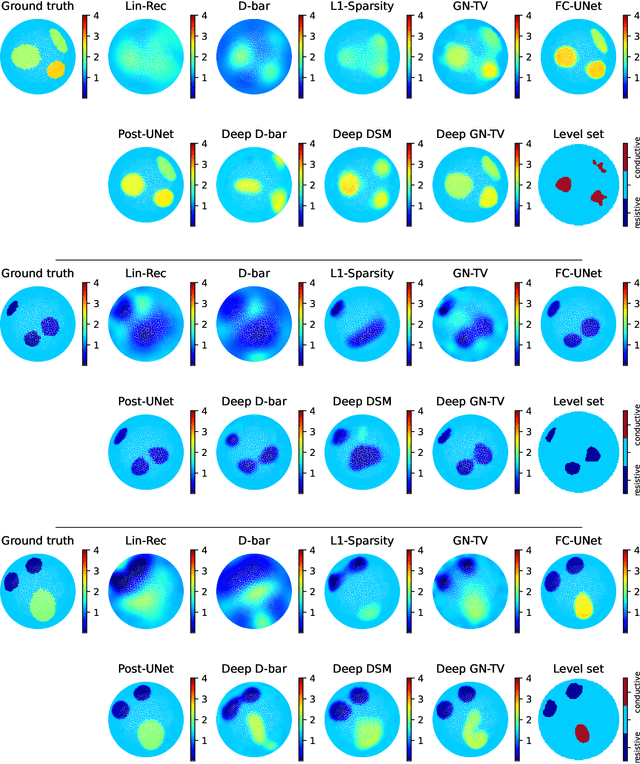
Electrical Impedance Tomography (EIT) is a powerful imaging modality widely used in medical diagnostics, industrial monitoring, and environmental studies. The EIT inverse problem is about inferring the internal conductivity distribution of the concerned object from the voltage measurements taken on its boundary. This problem is severely ill-posed, and requires advanced computational approaches for accurate and reliable image reconstruction. Recent innovations in both model-based reconstruction and deep learning have driven significant progress in the field. In this review, we explore learned reconstruction methods that employ deep neural networks for solving the EIT inverse problem. The discussion focuses on the complete electrode model, one popular mathematical model for real-world applications of EIT. We compare a wide variety of learned approaches, including fully-learned, post-processing and learned iterative methods, with several conventional model-based reconstruction techniques, e.g., sparsity regularization, regularized Gauss-Newton iteration and level set method. The evaluation is based on three datasets: a simulated dataset of ellipses, an out-of-distribution simulated dataset, and the KIT4 dataset, including real-world measurements. Our results demonstrate that learned methods outperform model-based methods for in-distribution data but face challenges in generalization, where hybrid methods exhibit a good balance of accuracy and adaptability.

An Iterative Deep Ritz Method for Monotone Elliptic Problems

In this work, we present a novel iterative deep Ritz method (IDRM) for solving a general class of elliptic problems. It is inspired by the iterative procedure for minimizing the loss during the training of the neural network, but at each step encodes the geometry of the underlying function space and incorporates a convex penalty to enhance the performance of the algorithm. The algorithm is applicable to elliptic problems involving a monotone operator (not necessarily of variational form) and does not impose any stringent regularity assumption on the solution. It improves several existing neural PDE solvers, e.g., physics informed neural network and deep Ritz method, in terms of the accuracy for the concerned class of elliptic problems. Further, we establish a convergence rate for the method using tools from geometry of Banach spaces and theory of monotone operators, and also analyze the learning error. To illustrate the effectiveness of the method, we present several challenging examples, including a comparative study with existing techniques.

Point Source Identification Using Singularity Enriched Neural Networks

The inverse problem of recovering point sources represents an important class of applied inverse problems. However, there is still a lack of neural network-based methods for point source identification, mainly due to the inherent solution singularity. In this work, we develop a novel algorithm to identify point sources, utilizing a neural network combined with a singularity enrichment technique. We employ the fundamental solution and neural networks to represent the singular and regular parts, respectively, and then minimize an empirical loss involving the intensities and locations of the unknown point sources, as well as the parameters of the neural network. Moreover, by combining the conditional stability argument of the inverse problem with the generalization error of the empirical loss, we conduct a rigorous error analysis of the algorithm. We demonstrate the effectiveness of the method with several challenging experiments.

Electrical Impedance Tomography: A Fair Comparative Study on Deep Learning and Analytic-based Approaches

Electrical Impedance Tomography (EIT) is a powerful imaging technique with diverse applications, e.g., medical diagnosis, industrial monitoring, and environmental studies. The EIT inverse problem is about inferring the internal conductivity distribution of an object from measurements taken on its boundary. It is severely ill-posed, necessitating advanced computational methods for accurate image reconstructions. Recent years have witnessed significant progress, driven by innovations in analytic-based approaches and deep learning. This review explores techniques for solving the EIT inverse problem, focusing on the interplay between contemporary deep learning-based strategies and classical analytic-based methods. Four state-of-the-art deep learning algorithms are rigorously examined, harnessing the representational capabilities of deep neural networks to reconstruct intricate conductivity distributions. In parallel, two analytic-based methods, rooted in mathematical formulations and regularisation techniques, are dissected for their strengths and limitations. These methodologies are evaluated through various numerical experiments, encompassing diverse scenarios that reflect real-world complexities. A suite of performance metrics is employed to assess the efficacy of these methods. These metrics collectively provide a nuanced understanding of the methods' ability to capture essential features and delineate complex conductivity patterns. One novel feature of the study is the incorporation of variable conductivity scenarios, introducing a level of heterogeneity that mimics textured inclusions. This departure from uniform conductivity assumptions mimics realistic scenarios where tissues or materials exhibit spatially varying electrical properties. Exploring how each method responds to such variable conductivity scenarios opens avenues for understanding their robustness and adaptability.

Steerable Conditional Diffusion for Out-of-Distribution Adaptation in Imaging Inverse Problems

Denoising diffusion models have emerged as the go-to framework for solving inverse problems in imaging. A critical concern regarding these models is their performance on out-of-distribution (OOD) tasks, which remains an under-explored challenge. Realistic reconstructions inconsistent with the measured data can be generated, hallucinating image features that are uniquely present in the training dataset. To simultaneously enforce data-consistency and leverage data-driven priors, we introduce a novel sampling framework called Steerable Conditional Diffusion. This framework adapts the denoising network specifically to the available measured data. Utilising our proposed method, we achieve substantial enhancements in OOD performance across diverse imaging modalities, advancing the robust deployment of denoising diffusion models in real-world applications.

Score-Based Generative Models for PET Image Reconstruction

Score-based generative models have demonstrated highly promising results for medical image reconstruction tasks in magnetic resonance imaging or computed tomography. However, their application to Positron Emission Tomography (PET) is still largely unexplored. PET image reconstruction involves a variety of challenges, including Poisson noise with high variance and a wide dynamic range. To address these challenges, we propose several PET-specific adaptations of score-based generative models. The proposed framework is developed for both 2D and 3D PET. In addition, we provide an extension to guided reconstruction using magnetic resonance images. We validate the approach through extensive 2D and 3D $\textit{in-silico}$ experiments with a model trained on patient-realistic data without lesions, and evaluate on data without lesions as well as out-of-distribution data with lesions. This demonstrates the proposed method's robustness and significant potential for improved PET reconstruction.

Solving Elliptic Optimal Control Problems using Physics Informed Neural Networks

In this work, we present and analyze a numerical solver for optimal control problems (without / with box constraint) for linear and semilinear second-order elliptic problems. The approach is based on a coupled system derived from the first-order optimality system of the optimal control problem, and applies physics informed neural networks (PINNs) to solve the coupled system. We present an error analysis of the numerical scheme, and provide $L^2(\Omega)$ error bounds on the state, control and adjoint state in terms of deep neural network parameters (e.g., depth, width, and parameter bounds) and the number of sampling points in the domain and on the boundary. The main tools in the analysis include offset Rademacher complexity and boundedness and Lipschitz continuity of neural network functions. We present several numerical examples to illustrate the approach and compare it with three existing approaches.

On the Approximation of Bi-Lipschitz Maps by Invertible Neural Networks

Invertible neural networks (INNs) represent an important class of deep neural network architectures that have been widely used in several applications. The universal approximation properties of INNs have also been established recently. However, the approximation rate of INNs is largely missing. In this work, we provide an analysis of the capacity of a class of coupling-based INNs to approximate bi-Lipschitz continuous mappings on a compact domain, and the result shows that it can well approximate both forward and inverse maps simultaneously. Furthermore, we develop an approach for approximating bi-Lipschitz maps on infinite-dimensional spaces that simultaneously approximate the forward and inverse maps, by combining model reduction with principal component analysis and INNs for approximating the reduced map, and we analyze the overall approximation error of the approach. Preliminary numerical results show the feasibility of the approach for approximating the solution operator for parameterized second-order elliptic problems.

Electrical Impedance Tomography with Deep Calderón Method

Electrical impedance tomography (EIT) is a noninvasive medical imaging modality utilizing the current-density/voltage data measured on the surface of the subject. Calder\'on's method is a relatively recent EIT imaging algorithm that is non-iterative, fast, and capable of reconstructing complex-valued electric impedances. However, due to the regularization via low-pass filtering and linearization, the reconstructed images suffer from severe blurring and underestimation of the exact conductivity values. In this work, we develop an enhanced version of Calder\'on's method, using convolution neural networks (i.e., U-net) via a postprocessing step. Specifically, we learn a U-net to postprocess the EIT images generated by Calder\'on's method so as to have better resolutions and more accurate estimates of conductivity values. We simulate chest configurations with which we generate the current-density/voltage boundary measurements and the corresponding reconstructed images by Calder\'on's method. With the paired training data, we learn the neural network and evaluate its performance on real tank measurement data. The experimental results indicate that the proposed approach indeed provides a fast and direct (complex-valued) impedance tomography imaging technique, and substantially improves the capability of the standard Calder\'on's method.