An Iterative Deep Ritz Method for Monotone Elliptic Problems

In this work, we present a novel iterative deep Ritz method (IDRM) for solving a general class of elliptic problems. It is inspired by the iterative procedure for minimizing the loss during the training of the neural network, but at each step encodes the geometry of the underlying function space and incorporates a convex penalty to enhance the performance of the algorithm. The algorithm is applicable to elliptic problems involving a monotone operator (not necessarily of variational form) and does not impose any stringent regularity assumption on the solution. It improves several existing neural PDE solvers, e.g., physics informed neural network and deep Ritz method, in terms of the accuracy for the concerned class of elliptic problems. Further, we establish a convergence rate for the method using tools from geometry of Banach spaces and theory of monotone operators, and also analyze the learning error. To illustrate the effectiveness of the method, we present several challenging examples, including a comparative study with existing techniques.

Point Source Identification Using Singularity Enriched Neural Networks

The inverse problem of recovering point sources represents an important class of applied inverse problems. However, there is still a lack of neural network-based methods for point source identification, mainly due to the inherent solution singularity. In this work, we develop a novel algorithm to identify point sources, utilizing a neural network combined with a singularity enrichment technique. We employ the fundamental solution and neural networks to represent the singular and regular parts, respectively, and then minimize an empirical loss involving the intensities and locations of the unknown point sources, as well as the parameters of the neural network. Moreover, by combining the conditional stability argument of the inverse problem with the generalization error of the empirical loss, we conduct a rigorous error analysis of the algorithm. We demonstrate the effectiveness of the method with several challenging experiments.

Self-playing Adversarial Language Game Enhances LLM Reasoning

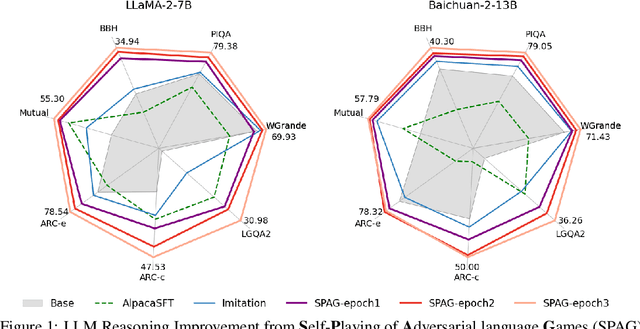
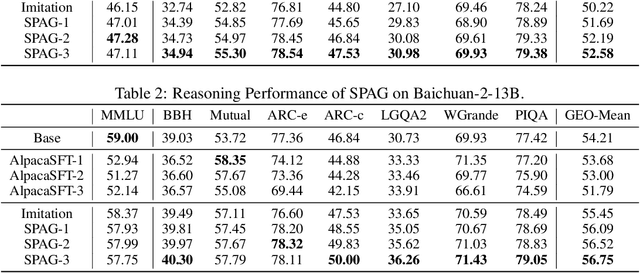
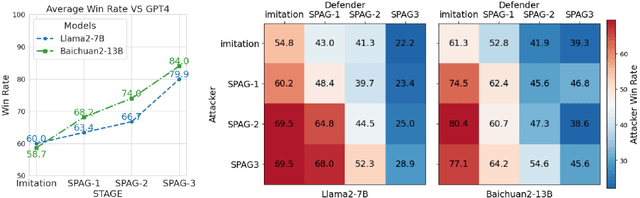
We explore the self-play training procedure of large language models (LLMs) in a two-player adversarial language game called Adversarial Taboo. In this game, an attacker and a defender communicate with respect to a target word only visible to the attacker. The attacker aims to induce the defender to utter the target word unconsciously, while the defender tries to infer the target word from the attacker's utterances. To win the game, both players should have sufficient knowledge about the target word and high-level reasoning ability to infer and express in this information-reserved conversation. Hence, we are curious about whether LLMs' reasoning ability can be further enhanced by Self-Play in this Adversarial language Game (SPAG). With this goal, we let LLMs act as the attacker and play with a copy of itself as the defender on an extensive range of target words. Through reinforcement learning on the game outcomes, we observe that the LLMs' performance uniformly improves on a broad range of reasoning benchmarks. Furthermore, iteratively adopting this self-play process can continuously promote LLM's reasoning ability. The code is at https://github.com/Linear95/SPAG.

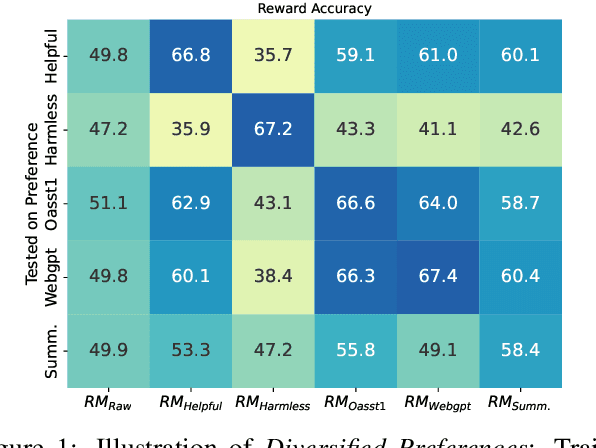
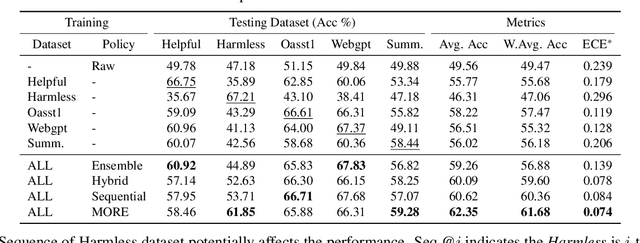
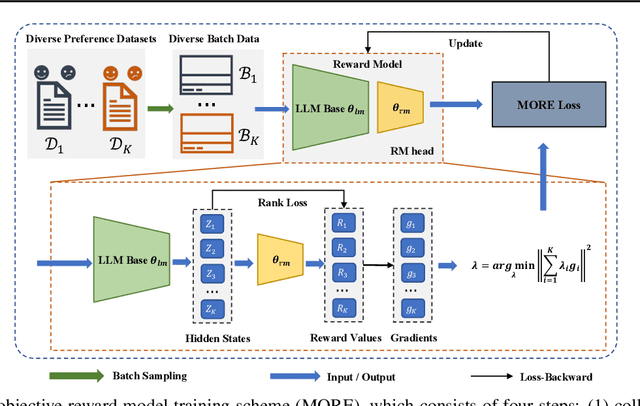
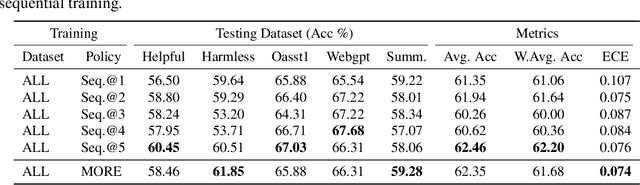
On Diversified Preferences of Large Language Model Alignment

Aligning large language models (LLMs) with human preferences has been recognized as the key to improving LLMs' interaction quality. However, in this pluralistic world, human preferences can be diversified by people's different tastes, which hinders the effectiveness of LLM alignment methods. In this paper, we provide the first quantitative analysis to verify the existence of diversified preferences in commonly used human feedback datasets. To mitigate the alignment ineffectiveness caused by diversified preferences, we propose a novel \textbf{M}ulti-\textbf{O}bjective \textbf{Re}ward learning method (MORE), which can automatically adjust the learning gradients across different preference data sources. In experiments, we evaluate MORE with the Pythia-1.4B model on five mixed human preference datasets, on which our method achieves superior performance compared with other baselines in terms of preference accuracy and prediction calibration.

Solving Elliptic Problems with Singular Sources using Singularity Splitting Deep Ritz Method

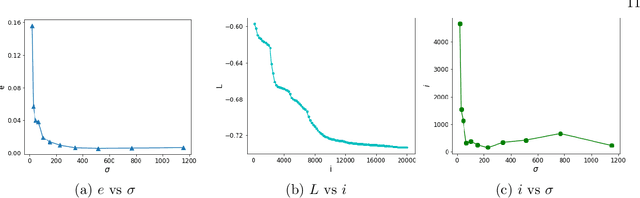
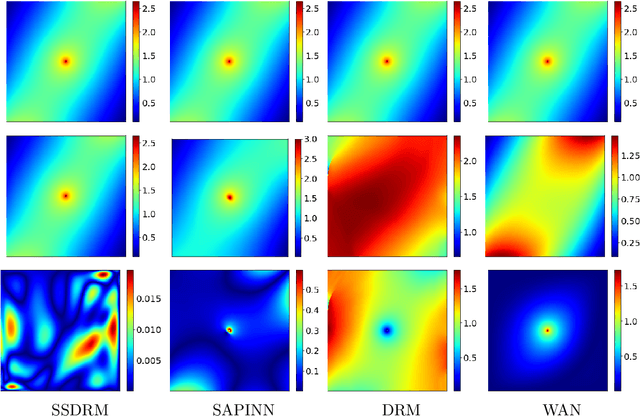
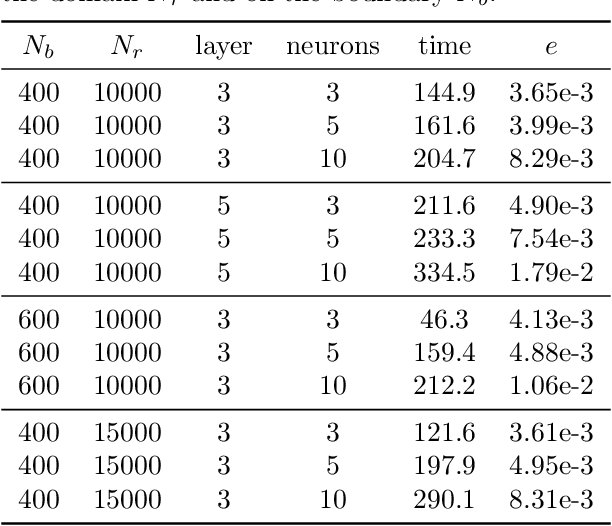
In this work, we develop an efficient solver based on deep neural networks for the Poisson equation with variable coefficients and singular sources expressed by the Dirac delta function $\delta(\mathbf{x})$. This class of problems covers general point sources, line sources and point-line combinations, and has a broad range of practical applications. The proposed approach is based on decomposing the true solution into a singular part that is known analytically using the fundamental solution of the Laplace equation and a regular part that satisfies a suitable elliptic PDE with smoother sources, and then solving for the regular part using the deep Ritz method. A path-following strategy is suggested to select the penalty parameter for penalizing the Dirichlet boundary condition. Extensive numerical experiments in two- and multi-dimensional spaces with point sources, line sources or their combinations are presented to illustrate the efficiency of the proposed approach, and a comparative study with several existing approaches is also given, which shows clearly its competitiveness for the specific class of problems. In addition, we briefly discuss the error analysis of the approach.