Deep Learning Based Reconstruction Methods for Electrical Impedance Tomography

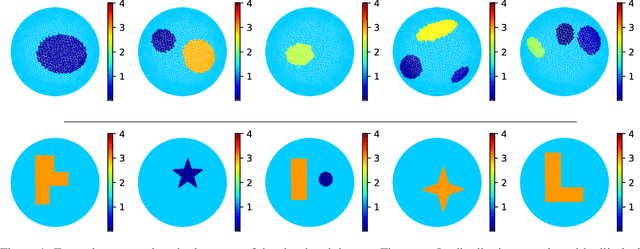
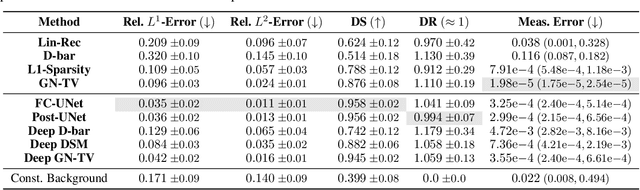
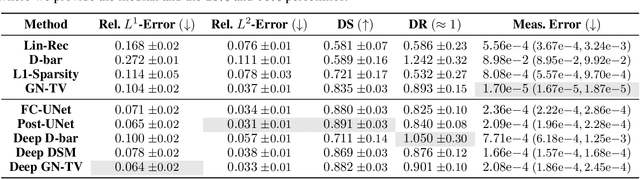
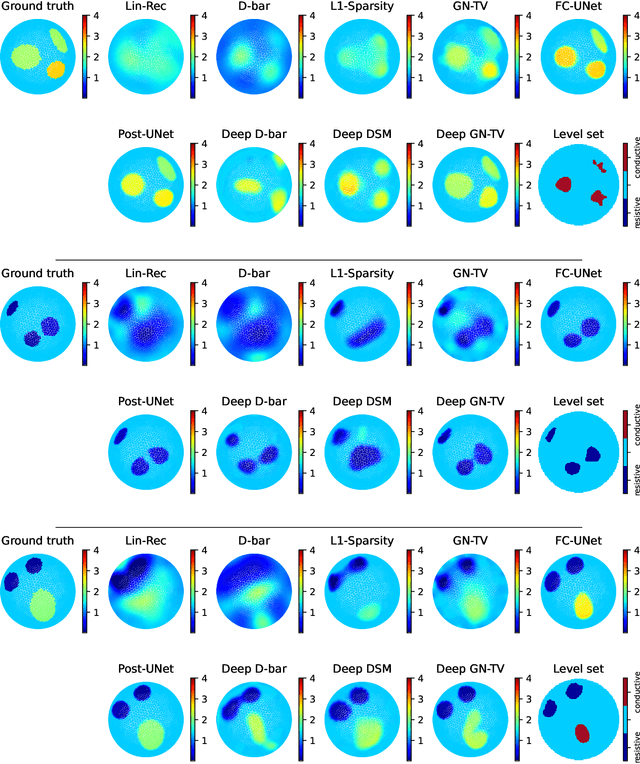
Electrical Impedance Tomography (EIT) is a powerful imaging modality widely used in medical diagnostics, industrial monitoring, and environmental studies. The EIT inverse problem is about inferring the internal conductivity distribution of the concerned object from the voltage measurements taken on its boundary. This problem is severely ill-posed, and requires advanced computational approaches for accurate and reliable image reconstruction. Recent innovations in both model-based reconstruction and deep learning have driven significant progress in the field. In this review, we explore learned reconstruction methods that employ deep neural networks for solving the EIT inverse problem. The discussion focuses on the complete electrode model, one popular mathematical model for real-world applications of EIT. We compare a wide variety of learned approaches, including fully-learned, post-processing and learned iterative methods, with several conventional model-based reconstruction techniques, e.g., sparsity regularization, regularized Gauss-Newton iteration and level set method. The evaluation is based on three datasets: a simulated dataset of ellipses, an out-of-distribution simulated dataset, and the KIT4 dataset, including real-world measurements. Our results demonstrate that learned methods outperform model-based methods for in-distribution data but face challenges in generalization, where hybrid methods exhibit a good balance of accuracy and adaptability.

Electrical Impedance Tomography: A Fair Comparative Study on Deep Learning and Analytic-based Approaches

Electrical Impedance Tomography (EIT) is a powerful imaging technique with diverse applications, e.g., medical diagnosis, industrial monitoring, and environmental studies. The EIT inverse problem is about inferring the internal conductivity distribution of an object from measurements taken on its boundary. It is severely ill-posed, necessitating advanced computational methods for accurate image reconstructions. Recent years have witnessed significant progress, driven by innovations in analytic-based approaches and deep learning. This review explores techniques for solving the EIT inverse problem, focusing on the interplay between contemporary deep learning-based strategies and classical analytic-based methods. Four state-of-the-art deep learning algorithms are rigorously examined, harnessing the representational capabilities of deep neural networks to reconstruct intricate conductivity distributions. In parallel, two analytic-based methods, rooted in mathematical formulations and regularisation techniques, are dissected for their strengths and limitations. These methodologies are evaluated through various numerical experiments, encompassing diverse scenarios that reflect real-world complexities. A suite of performance metrics is employed to assess the efficacy of these methods. These metrics collectively provide a nuanced understanding of the methods' ability to capture essential features and delineate complex conductivity patterns. One novel feature of the study is the incorporation of variable conductivity scenarios, introducing a level of heterogeneity that mimics textured inclusions. This departure from uniform conductivity assumptions mimics realistic scenarios where tissues or materials exhibit spatially varying electrical properties. Exploring how each method responds to such variable conductivity scenarios opens avenues for understanding their robustness and adaptability.

A Direct Sampling-Based Deep Learning Approach for Inverse Medium Scattering Problems

In this work, we focus on the inverse medium scattering problem (IMSP), which aims to recover unknown scatterers based on measured scattered data. Motivated by the efficient direct sampling method (DSM) introduced in [23], we propose a novel direct sampling-based deep learning approach (DSM-DL)for reconstructing inhomogeneous scatterers. In particular, we use the U-Net neural network to learn the relation between the index functions and the true contrasts. Our proposed DSM-DL is computationally efficient, robust to noise, easy to implement, and able to naturally incorporate multiple measured data to achieve high-quality reconstructions. Some representative tests are carried out with varying numbers of incident waves and different noise levels to evaluate the performance of the proposed method. The results demonstrate the promising benefits of combining deep learning techniques with the DSM for IMSP.

Deep Learning Methods for Partial Differential Equations and Related Parameter Identification Problems

Recent years have witnessed a growth in mathematics for deep learning--which seeks a deeper understanding of the concepts of deep learning with mathematics, and explores how to make it more robust--and deep learning for mathematics, where deep learning algorithms are used to solve problems in mathematics. The latter has popularised the field of scientific machine learning where deep learning is applied to problems in scientific computing. Specifically, more and more neural network architectures have been developed to solve specific classes of partial differential equations (PDEs). Such methods exploit properties that are inherent to PDEs and thus solve the PDEs better than classical feed-forward neural networks, recurrent neural networks, and convolutional neural networks. This has had a great impact in the area of mathematical modeling where parametric PDEs are widely used to model most natural and physical processes arising in science and engineering, In this work, we review such methods and extend them for parametric studies as well as for solving the related inverse problems. We equally proceed to show their relevance in some industrial applications.