Deep Learning Methods for Partial Differential Equations and Related Parameter Identification Problems

Recent years have witnessed a growth in mathematics for deep learning--which seeks a deeper understanding of the concepts of deep learning with mathematics, and explores how to make it more robust--and deep learning for mathematics, where deep learning algorithms are used to solve problems in mathematics. The latter has popularised the field of scientific machine learning where deep learning is applied to problems in scientific computing. Specifically, more and more neural network architectures have been developed to solve specific classes of partial differential equations (PDEs). Such methods exploit properties that are inherent to PDEs and thus solve the PDEs better than classical feed-forward neural networks, recurrent neural networks, and convolutional neural networks. This has had a great impact in the area of mathematical modeling where parametric PDEs are widely used to model most natural and physical processes arising in science and engineering, In this work, we review such methods and extend them for parametric studies as well as for solving the related inverse problems. We equally proceed to show their relevance in some industrial applications.

Deeply supervised UNet for semantic segmentation to assist dermatopathological assessment of Basal Cell Carcinoma (BCC)

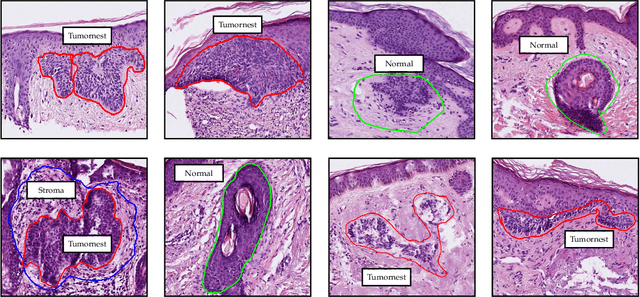
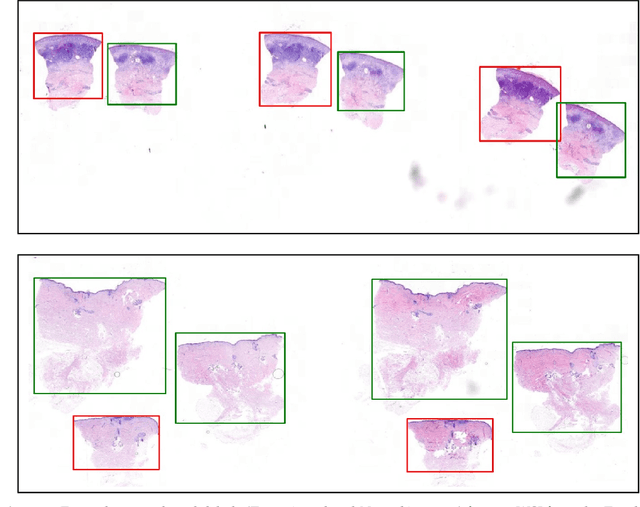
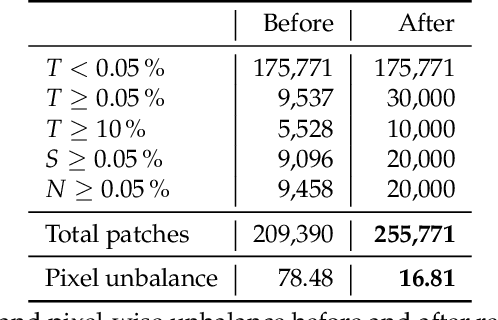
Accurate and fast assessment of resection margins is an essential part of a dermatopathologist's clinical routine. In this work, we successfully develop a deep learning method to assist the pathologists by marking critical regions that have a high probability of exhibiting pathological features in Whole Slide Images (WSI). We focus on detecting Basal Cell Carcinoma (BCC) through semantic segmentation using several models based on the UNet architecture. The study includes 650 WSI with 3443 tissue sections in total. Two clinical dermatopathologists annotated the data, marking tumor tissues' exact location on 100 WSI. The rest of the data, with ground-truth section-wise labels, is used to further validate and test the models. We analyze two different encoders for the first part of the UNet network and two additional training strategies: a) deep supervision, b) linear combination of decoder outputs, and obtain some interpretations about what the network's decoder does in each case. The best model achieves over 96%, accuracy, sensitivity, and specificity on the test set.