New universal operator approximation theorem for encoder-decoder architectures (Preprint)

Motivated by the rapidly growing field of mathematics for operator approximation with neural networks, we present a novel universal operator approximation theorem for a broad class of encoder-decoder architectures. In this study, we focus on approximating continuous operators in $\mathcal{C}(\mathcal{X}, \mathcal{Y})$, where $\mathcal{X}$ and $\mathcal{Y}$ are infinite-dimensional normed or metric spaces, and we consider uniform convergence on compact subsets of $\mathcal{X}$. Unlike standard results in the operator learning literature, we investigate the case where the approximating operator sequence can be chosen independently of the compact sets. Taking a topological perspective, we analyze different types of operator approximation and show that compact-set-independent approximation is a strictly stronger property in most relevant operator learning frameworks. To establish our results, we introduce a new approximation property tailored to encoder-decoder architectures, which enables us to prove a universal operator approximation theorem ensuring uniform convergence on every compact subset. This result unifies and extends existing universal operator approximation theorems for various encoder-decoder architectures, including classical DeepONets, BasisONets, special cases of MIONets, architectures based on frames and other related approaches.

Convergence Properties of Score-Based Models using Graduated Optimisation for Linear Inverse Problems

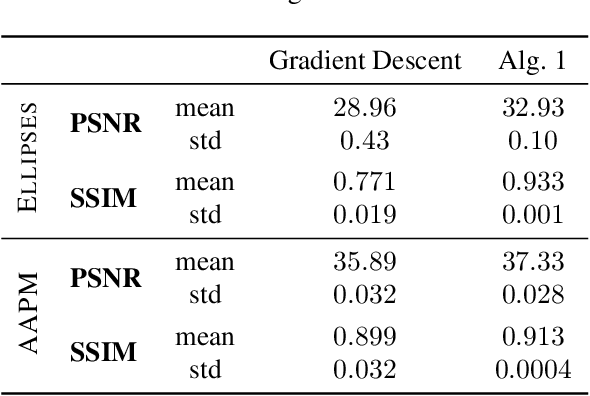
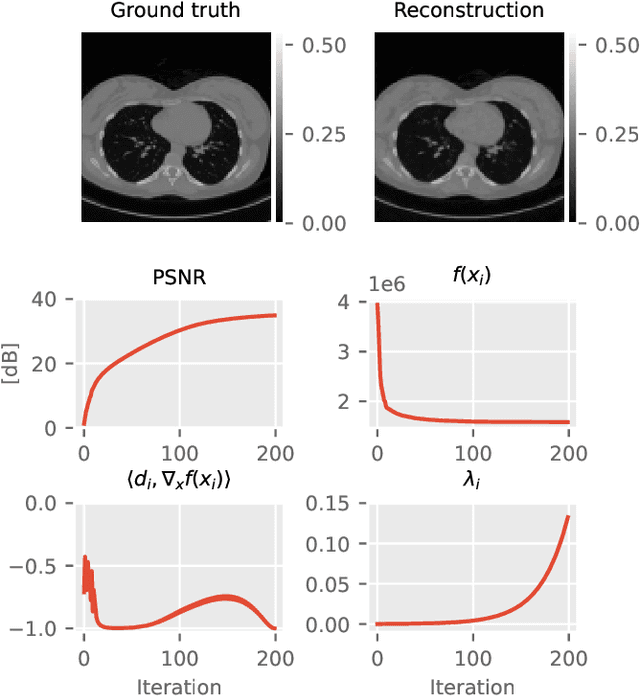
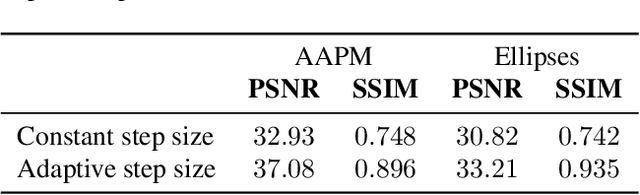
The incorporation of generative models as regularisers within variational formulations for inverse problems has proven effective across numerous image reconstruction tasks. However, the resulting optimisation problem is often non-convex and challenging to solve. In this work, we show that score-based generative models (SGMs) can be used in a graduated optimisation framework to solve inverse problems. We show that the resulting graduated non-convexity flow converge to stationary points of the original problem and provide a numerical convergence analysis of a 2D toy example. We further provide experiments on computed tomography image reconstruction, where we show that this framework is able to recover high-quality images, independent of the initial value. The experiments highlight the potential of using SGMs in graduated optimisation frameworks.

Spatially Coherent Clustering Based on Orthogonal Nonnegative Matrix Factorization

Classical approaches in cluster analysis are typically based on a feature space analysis. However, many applications lead to datasets with additional spatial information and a ground truth with spatially coherent classes, which will not necessarily be reconstructed well by standard clustering methods. Motivated by applications in hyperspectral imaging, we introduce in this work clustering models based on orthogonal nonnegative matrix factorization, which include an additional total variation (TV) regularization procedure on the cluster membership matrix to enforce the needed spatial coherence in the clusters. We propose several approaches with different optimization techniques, where the TV regularization is either performed as a subsequent postprocessing step or included into the clustering algorithm. Finally, we provide a numerical evaluation of all proposed methods on a hyperspectral dataset obtained from a matrix-assisted laser desorption/ionisation imaging measurement, which leads to significantly better clustering results compared to classical clustering models.

A Survey on Surrogate Approaches to Non-negative Matrix Factorization

Motivated by applications in hyperspectral imaging we investigate methods for approximating a high-dimensional non-negative matrix $\mathbf{\mathit{Y}}$ by a product of two lower-dimensional, non-negative matrices $\mathbf{\mathit{K}}$ and $\mathbf{\mathit{X}}.$ This so-called non-negative matrix factorization is based on defining suitable Tikhonov functionals, which combine a discrepancy measure for $\mathbf{\mathit{Y}}\approx\mathbf{\mathit{KX}}$ with penalty terms for enforcing additional properties of $\mathbf{\mathit{K}}$ and $\mathbf{\mathit{X}}$. The minimization is based on alternating minimization with respect to $\mathbf{\mathit{K}}$ or $\mathbf{\mathit{X}}$, where in each iteration step one replaces the original Tikhonov functional by a locally defined surrogate functional. The choice of surrogate functionals is crucial: It should allow a comparatively simple minimization and simultaneously its first order optimality condition should lead to multiplicative update rules, which automatically preserve non-negativity of the iterates. We review the most standard construction principles for surrogate functionals for Frobenius-norm and Kullback-Leibler discrepancy measures. We extend the known surrogate constructions by a general framework, which allows to add a large variety of penalty terms. The paper finishes by deriving the corresponding alternating minimization schemes explicitely and by applying these methods to MALDI imaging data.

Analysis of Invariance and Robustness via Invertibility of ReLU-Networks

Studying the invertibility of deep neural networks (DNNs) provides a principled approach to better understand the behavior of these powerful models. Despite being a promising diagnostic tool, a consistent theory on their invertibility is still lacking. We derive a theoretically motivated approach to explore the preimages of ReLU-layers and mechanisms affecting the stability of the inverse. Using the developed theory, we numerically show how this approach uncovers characteristic properties of the network.