Conditional Feature Importance with Generative Modeling Using Adversarial Random Forests

This paper proposes a method for measuring conditional feature importance via generative modeling. In explainable artificial intelligence (XAI), conditional feature importance assesses the impact of a feature on a prediction model's performance given the information of other features. Model-agnostic post hoc methods to do so typically evaluate changes in the predictive performance under on-manifold feature value manipulations. Such procedures require creating feature values that respect conditional feature distributions, which can be challenging in practice. Recent advancements in generative modeling can facilitate this. For tabular data, which may consist of both categorical and continuous features, the adversarial random forest (ARF) stands out as a generative model that can generate on-manifold data points without requiring intensive tuning efforts or computational resources, making it a promising candidate model for subroutines in XAI methods. This paper proposes cARFi (conditional ARF feature importance), a method for measuring conditional feature importance through feature values sampled from ARF-estimated conditional distributions. cARFi requires only little tuning to yield robust importance scores that can flexibly adapt for conditional or marginal notions of feature importance, including straightforward extensions to condition on feature subsets and allows for inferring the significance of feature importances through statistical tests.

Data-driven advice for interpreting local and global model predictions in bioinformatics problems

Tree-based algorithms such as random forests and gradient boosted trees continue to be among the most popular and powerful machine learning models used across multiple disciplines. The conventional wisdom of estimating the impact of a feature in tree based models is to measure the \textit{node-wise reduction of a loss function}, which (i) yields only global importance measures and (ii) is known to suffer from severe biases. Conditional feature contributions (CFCs) provide \textit{local}, case-by-case explanations of a prediction by following the decision path and attributing changes in the expected output of the model to each feature along the path. However, Lundberg et al. pointed out a potential bias of CFCs which depends on the distance from the root of a tree. The by now immensely popular alternative, SHapley Additive exPlanation (SHAP) values appear to mitigate this bias but are computationally much more expensive. Here we contribute a thorough comparison of the explanations computed by both methods on a set of 164 publicly available classification problems in order to provide data-driven algorithm recommendations to current researchers. For random forests, we find extremely high similarities and correlations of both local and global SHAP values and CFC scores, leading to very similar rankings and interpretations. Analogous conclusions hold for the fidelity of using global feature importance scores as a proxy for the predictive power associated with each feature.

From unbiased MDI Feature Importance to Explainable AI for Trees

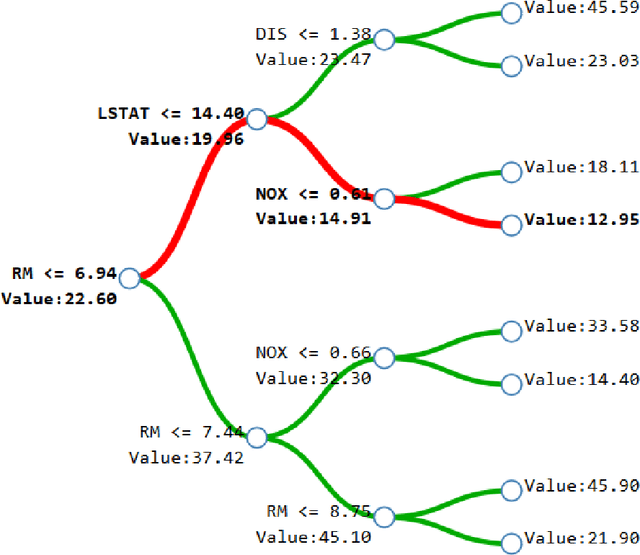
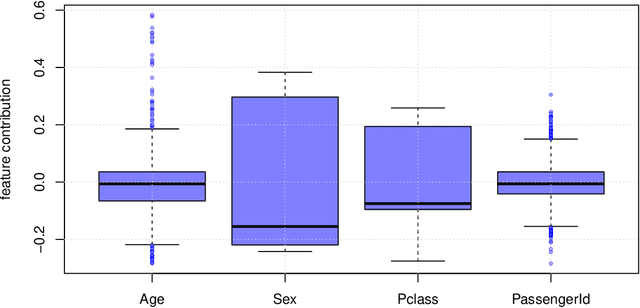
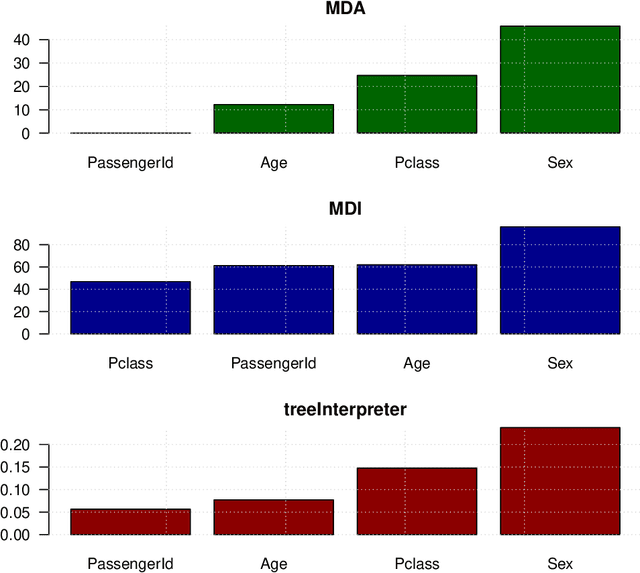
We attempt to give a unifying view of the various recent attempts to (i) improve the interpretability of tree-based models and (ii) debias the the default variable-importance measure in random Forests, Gini importance. In particular, we demonstrate a common thread among the out-of-bag based bias correction methods and their connection to local explanation for trees. In addition, we point out a bias caused by the inclusion of inbag data in the newly developed explainable AI for trees algorithms.

Unbiased variable importance for random forests

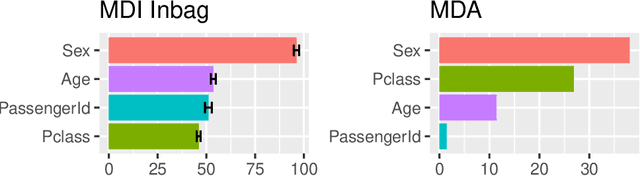
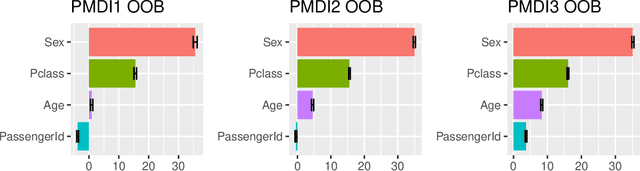
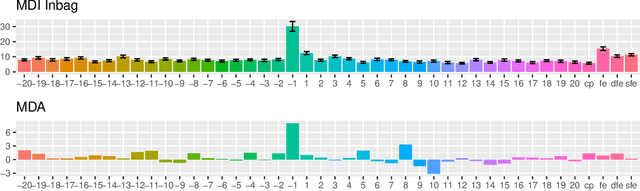
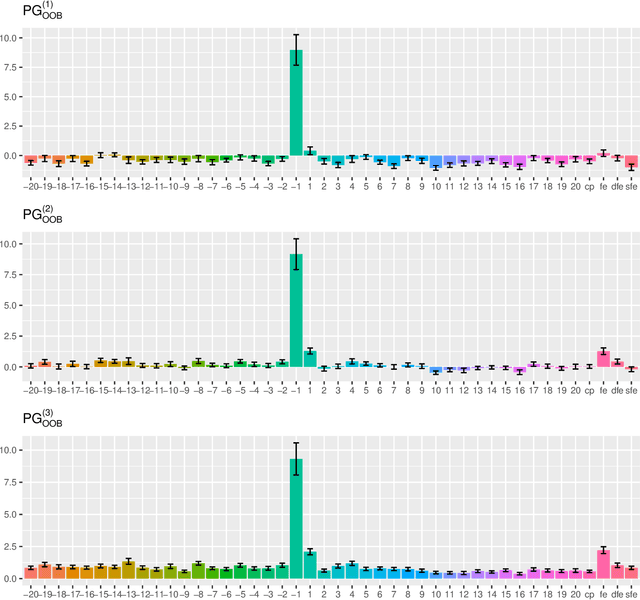
The default variable-importance measure in random Forests, Gini importance, has been shown to suffer from the bias of the underlying Gini-gain splitting criterion. While the alternative permutation importance is generally accepted as a reliable measure of variable importance, it is also computationally demanding and suffers from other shortcomings. We propose a simple solution to the misleading/untrustworthy Gini importance which can be viewed as an overfitting problem: we compute the loss reduction on the out-of-bag instead of the in-bag training samples.