Jan Kapar
Can synthetic data reproduce real-world findings in epidemiology? A replication study using tree-based generative AI
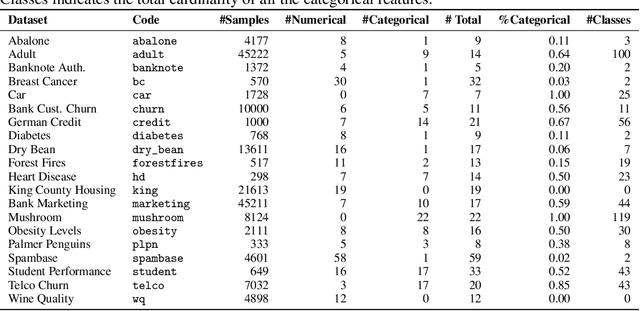
Aug 19, 2025Abstract:Generative artificial intelligence for synthetic data generation holds substantial potential to address practical challenges in epidemiology. However, many current methods suffer from limited quality, high computational demands, and complexity for non-experts. Furthermore, common evaluation strategies for synthetic data often fail to directly reflect statistical utility. Against this background, a critical underexplored question is whether synthetic data can reliably reproduce key findings from epidemiological research. We propose the use of adversarial random forests (ARF) as an efficient and convenient method for synthesizing tabular epidemiological data. To evaluate its performance, we replicated statistical analyses from six epidemiological publications and compared original with synthetic results. These publications cover blood pressure, anthropometry, myocardial infarction, accelerometry, loneliness, and diabetes, based on data from the German National Cohort (NAKO Gesundheitsstudie), the Bremen STEMI Registry U45 Study, and the Guelph Family Health Study. Additionally, we assessed the impact of dimensionality and variable complexity on synthesis quality by limiting datasets to variables relevant for individual analyses, including necessary derivations. Across all replicated original studies, results from multiple synthetic data replications consistently aligned with original findings. Even for datasets with relatively low sample size-to-dimensionality ratios, the replication outcomes closely matched the original results across various descriptive and inferential analyses. Reducing dimensionality and pre-deriving variables further enhanced both quality and stability of the results.
Autoencoding Random Forests
May 27, 2025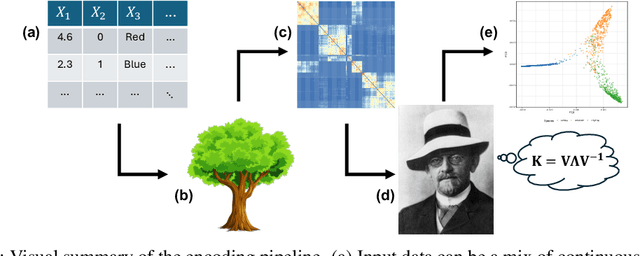

Abstract:We propose a principled method for autoencoding with random forests. Our strategy builds on foundational results from nonparametric statistics and spectral graph theory to learn a low-dimensional embedding of the model that optimally represents relationships in the data. We provide exact and approximate solutions to the decoding problem via constrained optimization, split relabeling, and nearest neighbors regression. These methods effectively invert the compression pipeline, establishing a map from the embedding space back to the input space using splits learned by the ensemble's constituent trees. The resulting decoders are universally consistent under common regularity assumptions. The procedure works with supervised or unsupervised models, providing a window into conditional or joint distributions. We demonstrate various applications of this autoencoder, including powerful new tools for visualization, compression, clustering, and denoising. Experiments illustrate the ease and utility of our method in a wide range of settings, including tabular, image, and genomic data.
What's Wrong with Your Synthetic Tabular Data? Using Explainable AI to Evaluate Generative Models
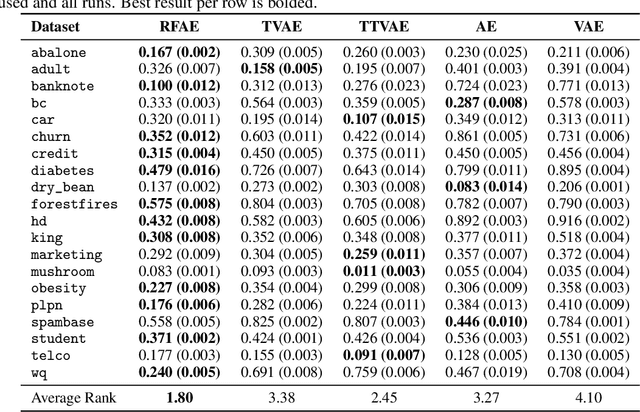
Apr 29, 2025Abstract:Evaluating synthetic tabular data is challenging, since they can differ from the real data in so many ways. There exist numerous metrics of synthetic data quality, ranging from statistical distances to predictive performance, often providing conflicting results. Moreover, they fail to explain or pinpoint the specific weaknesses in the synthetic data. To address this, we apply explainable AI (XAI) techniques to a binary detection classifier trained to distinguish real from synthetic data. While the classifier identifies distributional differences, XAI concepts such as feature importance and feature effects, analyzed through methods like permutation feature importance, partial dependence plots, Shapley values and counterfactual explanations, reveal why synthetic data are distinguishable, highlighting inconsistencies, unrealistic dependencies, or missing patterns. This interpretability increases transparency in synthetic data evaluation and provides deeper insights beyond conventional metrics, helping diagnose and improve synthetic data quality. We apply our approach to two tabular datasets and generative models, showing that it uncovers issues overlooked by standard evaluation techniques.
Conditional Feature Importance with Generative Modeling Using Adversarial Random Forests
Jan 19, 2025Abstract:This paper proposes a method for measuring conditional feature importance via generative modeling. In explainable artificial intelligence (XAI), conditional feature importance assesses the impact of a feature on a prediction model's performance given the information of other features. Model-agnostic post hoc methods to do so typically evaluate changes in the predictive performance under on-manifold feature value manipulations. Such procedures require creating feature values that respect conditional feature distributions, which can be challenging in practice. Recent advancements in generative modeling can facilitate this. For tabular data, which may consist of both categorical and continuous features, the adversarial random forest (ARF) stands out as a generative model that can generate on-manifold data points without requiring intensive tuning efforts or computational resources, making it a promising candidate model for subroutines in XAI methods. This paper proposes cARFi (conditional ARF feature importance), a method for measuring conditional feature importance through feature values sampled from ARF-estimated conditional distributions. cARFi requires only little tuning to yield robust importance scores that can flexibly adapt for conditional or marginal notions of feature importance, including straightforward extensions to condition on feature subsets and allows for inferring the significance of feature importances through statistical tests.
CountARFactuals -- Generating plausible model-agnostic counterfactual explanations with adversarial random forests
Apr 04, 2024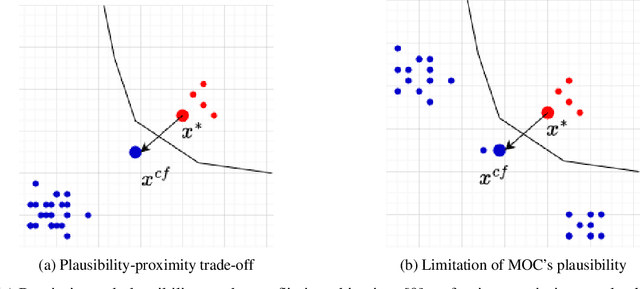


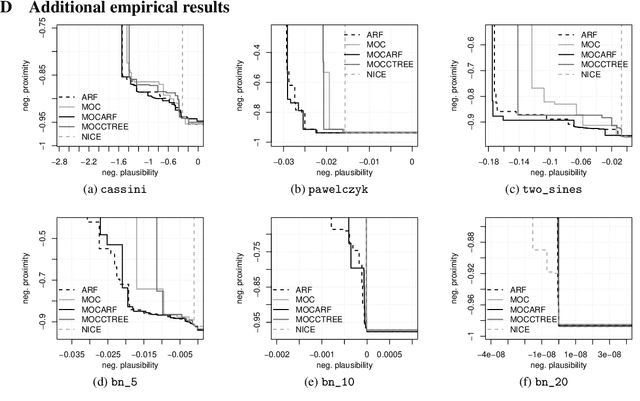
Abstract:Counterfactual explanations elucidate algorithmic decisions by pointing to scenarios that would have led to an alternative, desired outcome. Giving insight into the model's behavior, they hint users towards possible actions and give grounds for contesting decisions. As a crucial factor in achieving these goals, counterfactuals must be plausible, i.e., describing realistic alternative scenarios within the data manifold. This paper leverages a recently developed generative modeling technique -- adversarial random forests (ARFs) -- to efficiently generate plausible counterfactuals in a model-agnostic way. ARFs can serve as a plausibility measure or directly generate counterfactual explanations. Our ARF-based approach surpasses the limitations of existing methods that aim to generate plausible counterfactual explanations: It is easy to train and computationally highly efficient, handles continuous and categorical data naturally, and allows integrating additional desiderata such as sparsity in a straightforward manner.
Smooth densities and generative modeling with unsupervised random forests
May 19, 2022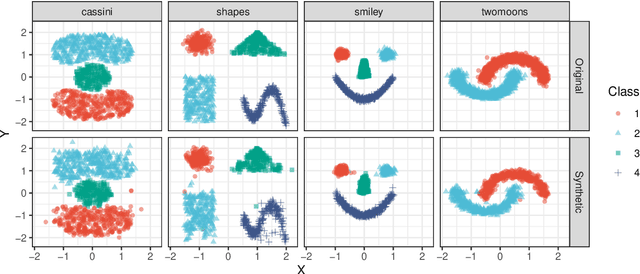
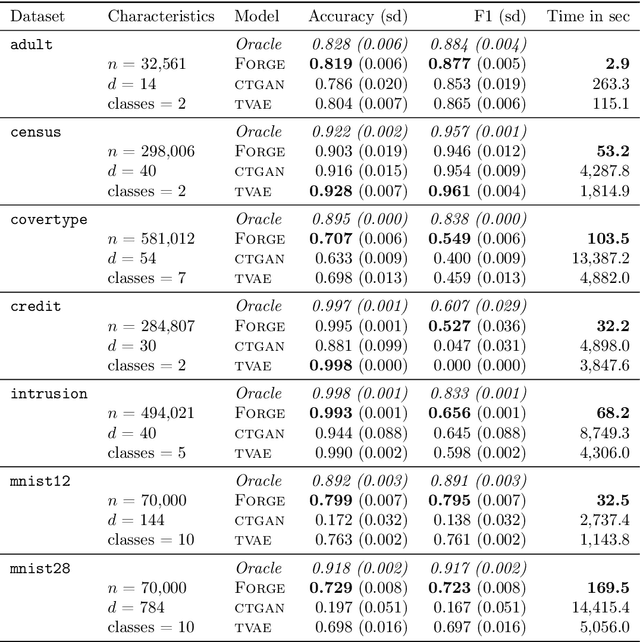
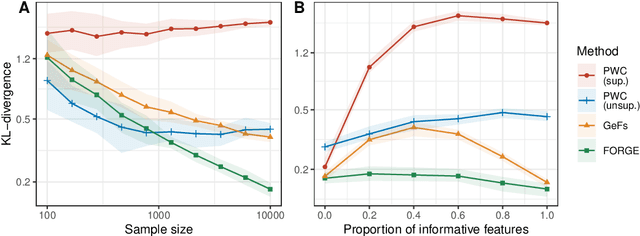
Abstract:Density estimation is a fundamental problem in statistics, and any attempt to do so in high dimensions typically requires strong assumptions or complex deep learning architectures. An important application for density estimators is synthetic data generation, an area currently dominated by neural networks that often demand enormous training datasets and extensive tuning. We propose a new method based on unsupervised random forests for estimating smooth densities in arbitrary dimensions without parametric constraints, as well as generating realistic synthetic data. We prove the consistency of our approach and demonstrate its advantages over existing tree-based density estimators, which generally rely on ill-chosen split criteria and do not scale well with data dimensionality. Experiments illustrate that our algorithm compares favorably to state-of-the-art deep learning generative models, achieving superior performance in a range of benchmark trials while executing about two orders of magnitude faster on average. Our method is implemented in easy-to-use $\texttt{R}$ and Python packages.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge