Relating the Partial Dependence Plot and Permutation Feature Importance to the Data Generating Process
Paper and Code
Sep 03, 2021
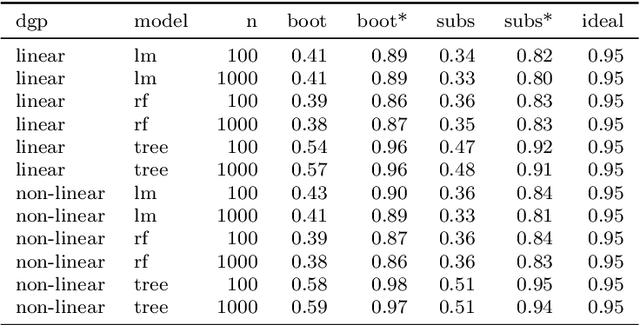
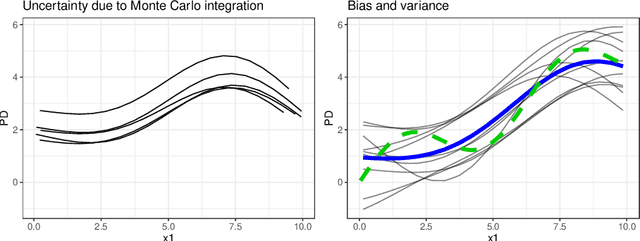
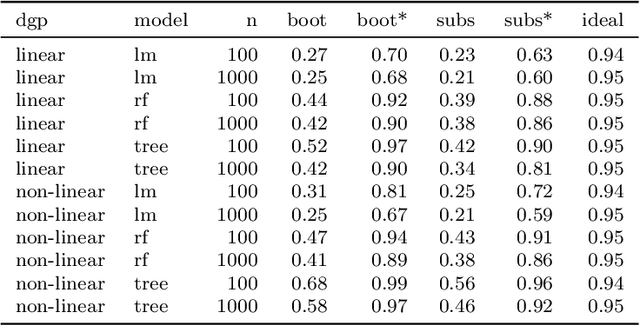
Scientists and practitioners increasingly rely on machine learning to model data and draw conclusions. Compared to statistical modeling approaches, machine learning makes fewer explicit assumptions about data structures, such as linearity. However, their model parameters usually cannot be easily related to the data generating process. To learn about the modeled relationships, partial dependence (PD) plots and permutation feature importance (PFI) are often used as interpretation methods. However, PD and PFI lack a theory that relates them to the data generating process. We formalize PD and PFI as statistical estimators of ground truth estimands rooted in the data generating process. We show that PD and PFI estimates deviate from this ground truth due to statistical biases, model variance and Monte Carlo approximation errors. To account for model variance in PD and PFI estimation, we propose the learner-PD and the learner-PFI based on model refits, and propose corrected variance and confidence interval estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge