Gamma-Nets: Generalizing Value Estimation over Timescale
Paper and Code
Nov 23, 2019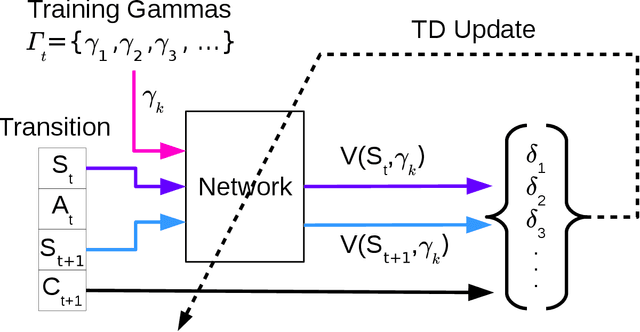
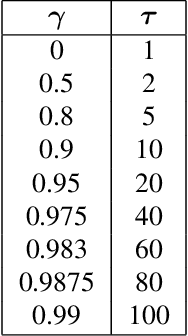
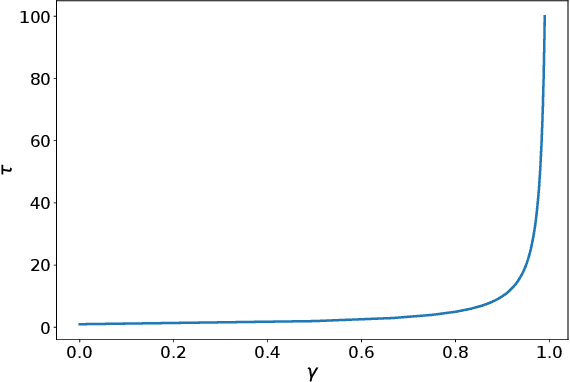

We present $\Gamma$-nets, a method for generalizing value function estimation over timescale. By using the timescale as one of the estimator's inputs we can estimate value for arbitrary timescales. As a result, the prediction target for any timescale is available and we are free to train on multiple timescales at each timestep. Here we empirically evaluate $\Gamma$-nets in the policy evaluation setting. We first demonstrate the approach on a square wave and then on a robot arm using linear function approximation. Next, we consider the deep reinforcement learning setting using several Atari video games. Our results show that $\Gamma$-nets can be effective for predicting arbitrary timescales, with only a small cost in accuracy as compared to learning estimators for fixed timescales. $\Gamma$-nets provide a method for compactly making predictions at many timescales without requiring a priori knowledge of the task, making it a valuable contribution to ongoing work on model-based planning, representation learning, and lifelong learning algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge