Reward-Respecting Subtasks for Model-Based Reinforcement Learning

To achieve the ambitious goals of artificial intelligence, reinforcement learning must include planning with a model of the world that is abstract in state and time. Deep learning has made progress in state abstraction, but, although the theory of time abstraction has been extensively developed based on the options framework, in practice options have rarely been used in planning. One reason for this is that the space of possible options is immense and the methods previously proposed for option discovery do not take into account how the option models will be used in planning. Options are typically discovered by posing subsidiary tasks such as reaching a bottleneck state, or maximizing a sensory signal other than the reward. Each subtask is solved to produce an option, and then a model of the option is learned and made available to the planning process. The subtasks proposed in most previous work ignore the reward on the original problem, whereas we propose subtasks that use the original reward plus a bonus based on a feature of the state at the time the option stops. We show that options and option models obtained from such reward-respecting subtasks are much more likely to be useful in planning and can be learned online and off-policy using existing learning algorithms. Reward respecting subtasks strongly constrain the space of options and thereby also provide a partial solution to the problem of option discovery. Finally, we show how the algorithms for learning values, policies, options, and models can be unified using general value functions.

Multi-step Reinforcement Learning: A Unifying Algorithm

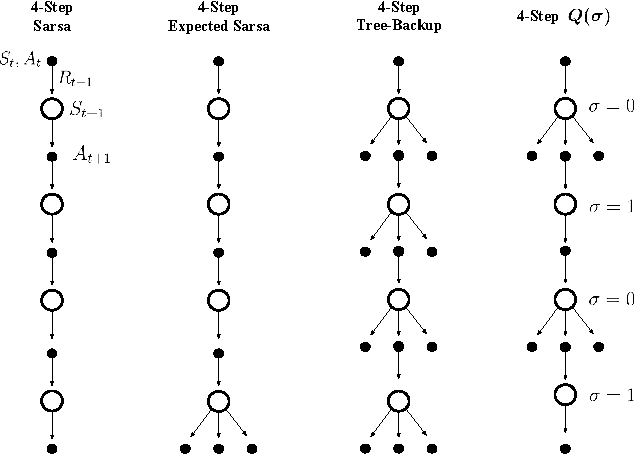
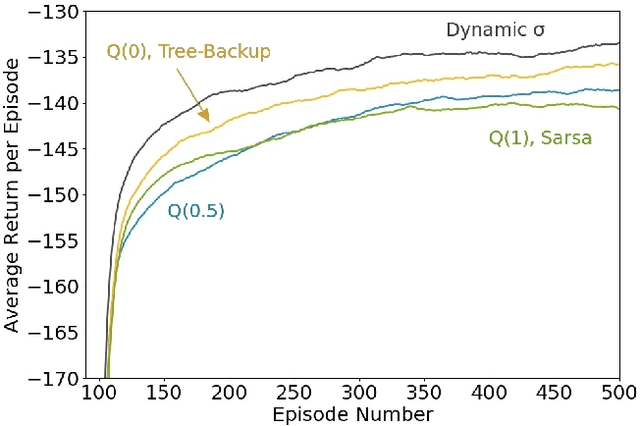
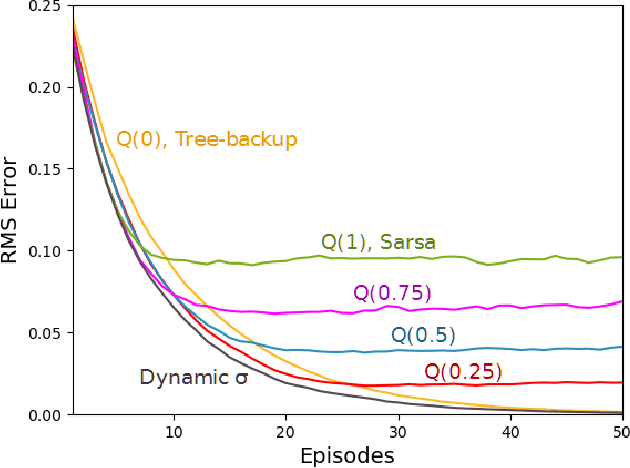
Unifying seemingly disparate algorithmic ideas to produce better performing algorithms has been a longstanding goal in reinforcement learning. As a primary example, TD($\lambda$) elegantly unifies one-step TD prediction with Monte Carlo methods through the use of eligibility traces and the trace-decay parameter $\lambda$. Currently, there are a multitude of algorithms that can be used to perform TD control, including Sarsa, $Q$-learning, and Expected Sarsa. These methods are often studied in the one-step case, but they can be extended across multiple time steps to achieve better performance. Each of these algorithms is seemingly distinct, and no one dominates the others for all problems. In this paper, we study a new multi-step action-value algorithm called $Q(\sigma)$ which unifies and generalizes these existing algorithms, while subsuming them as special cases. A new parameter, $\sigma$, is introduced to allow the degree of sampling performed by the algorithm at each step during its backup to be continuously varied, with Sarsa existing at one extreme (full sampling), and Expected Sarsa existing at the other (pure expectation). $Q(\sigma)$ is generally applicable to both on- and off-policy learning, but in this work we focus on experiments in the on-policy case. Our results show that an intermediate value of $\sigma$, which results in a mixture of the existing algorithms, performs better than either extreme. The mixture can also be varied dynamically which can result in even greater performance.

The Effect of Planning Shape on Dyna-style Planning in High-dimensional State Spaces

Dyna is an architecture for reinforcement learning agents that interleaves planning, acting, and learning in an online setting. This architecture aims to make fuller use of limited experience to achieve better performance with fewer environmental interactions. Dyna has been well studied in problems with a tabular representation of states, and has also been extended to some settings with larger state spaces that require function approximation. However, little work has studied Dyna in environments with high-dimensional state spaces like images. In Dyna, the environment model is typically used to generate one-step transitions from selected start states. We applied one-step Dyna to several games from the Arcade Learning Environment and found that the model-based updates offered surprisingly little benefit, even with a perfect model. However, when the model was used to generate longer trajectories of simulated experience, performance improved dramatically. This observation also holds when using a model that is learned from experience; even though the learned model is flawed, it can still be used to accelerate learning.