Kristopher De Asis
Value-aware Importance Weighting for Off-policy Reinforcement Learning
Jun 27, 2023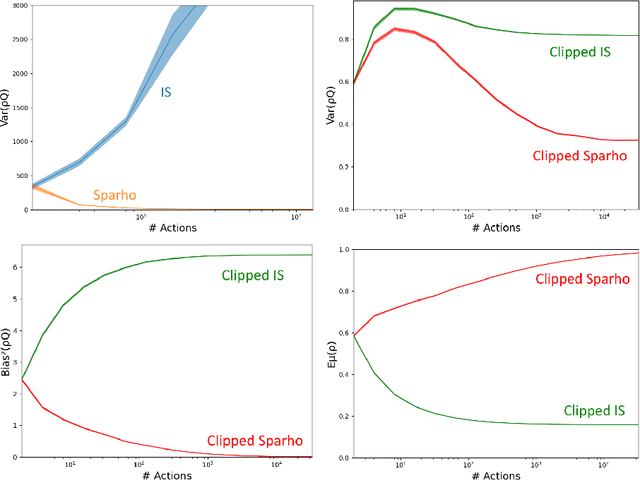
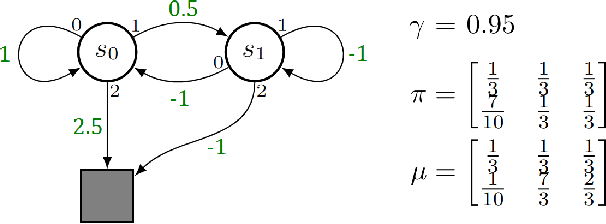
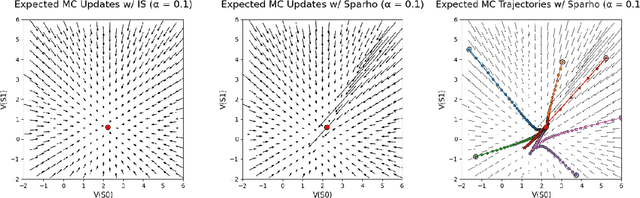
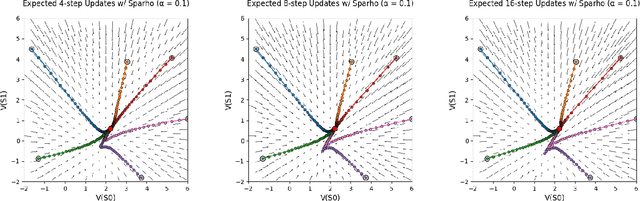
Abstract:Importance sampling is a central idea underlying off-policy prediction in reinforcement learning. It provides a strategy for re-weighting samples from a distribution to obtain unbiased estimates under another distribution. However, importance sampling weights tend to exhibit extreme variance, often leading to stability issues in practice. In this work, we consider a broader class of importance weights to correct samples in off-policy learning. We propose the use of $\textit{value-aware importance weights}$ which take into account the sample space to provide lower variance, but still unbiased, estimates under a target distribution. We derive how such weights can be computed, and detail key properties of the resulting importance weights. We then extend several reinforcement learning prediction algorithms to the off-policy setting with these weights, and evaluate them empirically.
Fixed-Horizon Temporal Difference Methods for Stable Reinforcement Learning
Sep 09, 2019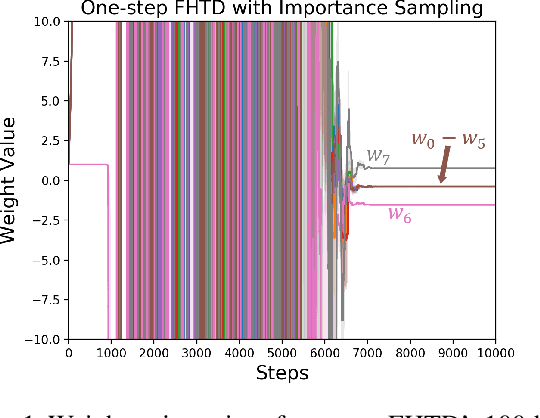


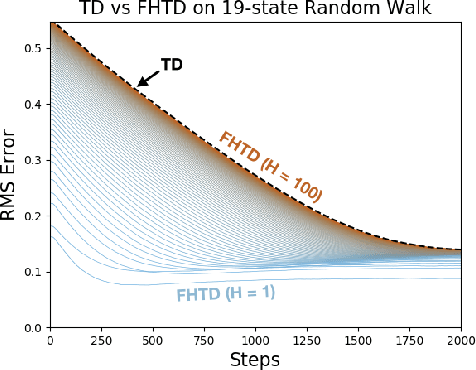
Abstract:We explore fixed-horizon temporal difference (TD) methods, reinforcement learning algorithms for a new kind of value function that predicts the sum of rewards over a $\textit{fixed}$ number of future time steps. To learn the value function for horizon $h$, these algorithms bootstrap from the value function for horizon $h-1$, or some shorter horizon. Because no value function bootstraps from itself, fixed-horizon methods are immune to the stability problems that plague other off-policy TD methods using function approximation (also known as "the deadly triad"). Although fixed-horizon methods require the storage of additional value functions, this gives the agent additional predictive power, while the added complexity can be substantially reduced via parallel updates, shared weights, and $n$-step bootstrapping. We show how to use fixed-horizon value functions to solve reinforcement learning problems competitively with methods such as Q-learning that learn conventional value functions. We also prove convergence of fixed-horizon temporal difference methods with linear and general function approximation. Taken together, our results establish fixed-horizon TD methods as a viable new way of avoiding the stability problems of the deadly triad.
Predicting Periodicity with Temporal Difference Learning
Sep 20, 2018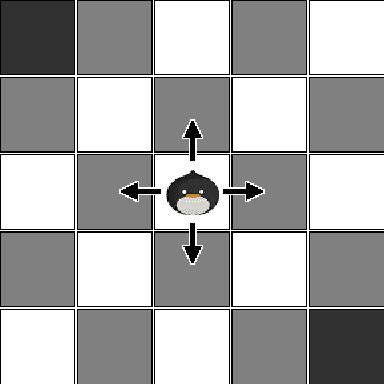
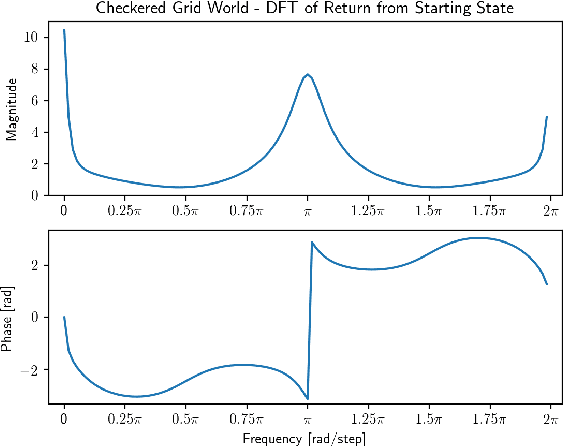
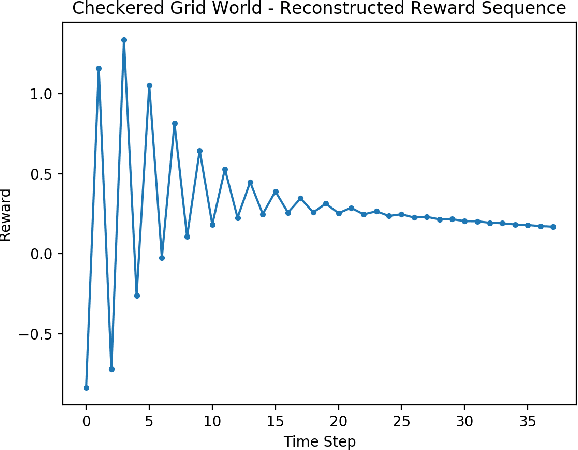
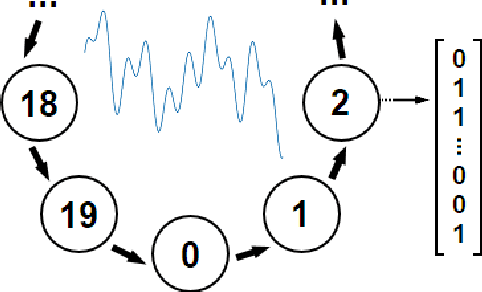
Abstract:Temporal difference (TD) learning is an important approach in reinforcement learning, as it combines ideas from dynamic programming and Monte Carlo methods in a way that allows for online and incremental model-free learning. A key idea of TD learning is that it is learning predictive knowledge about the environment in the form of value functions, from which it can derive its behavior to address long-term sequential decision making problems. The agent's horizon of interest, that is, how immediate or long-term a TD learning agent predicts into the future, is adjusted through a discount rate parameter. In this paper, we introduce an alternative view on the discount rate, with insight from digital signal processing, to include complex-valued discounting. Our results show that setting the discount rate to appropriately chosen complex numbers allows for online and incremental estimation of the Discrete Fourier Transform (DFT) of a signal of interest with TD learning. We thereby extend the types of knowledge representable by value functions, which we show are particularly useful for identifying periodic effects in the reward sequence.
Per-decision Multi-step Temporal Difference Learning with Control Variates
Jul 05, 2018



Abstract:Multi-step temporal difference (TD) learning is an important approach in reinforcement learning, as it unifies one-step TD learning with Monte Carlo methods in a way where intermediate algorithms can outperform either extreme. They address a bias-variance trade off between reliance on current estimates, which could be poor, and incorporating longer sampled reward sequences into the updates. Especially in the off-policy setting, where the agent aims to learn about a policy different from the one generating its behaviour, the variance in the updates can cause learning to diverge as the number of sampled rewards used in the estimates increases. In this paper, we introduce per-decision control variates for multi-step TD algorithms, and compare them to existing methods. Our results show that including the control variates can greatly improve performance on both on and off-policy multi-step temporal difference learning tasks.
Multi-step Reinforcement Learning: A Unifying Algorithm
Jun 11, 2018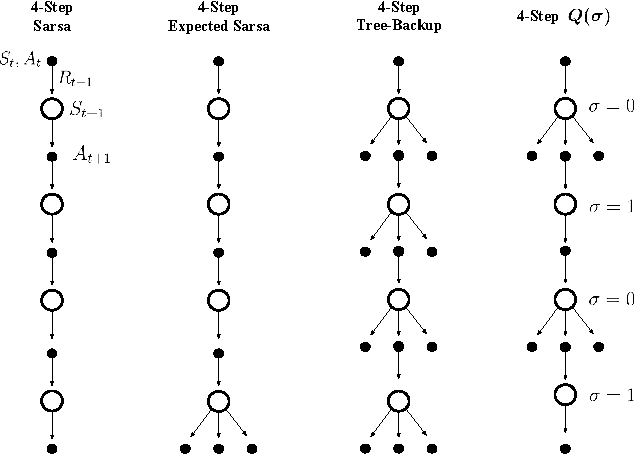
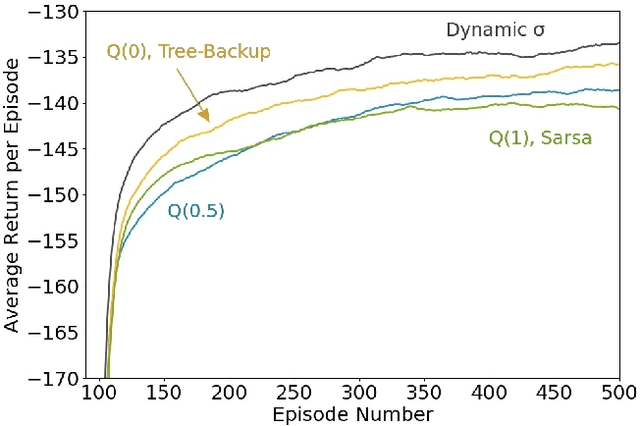

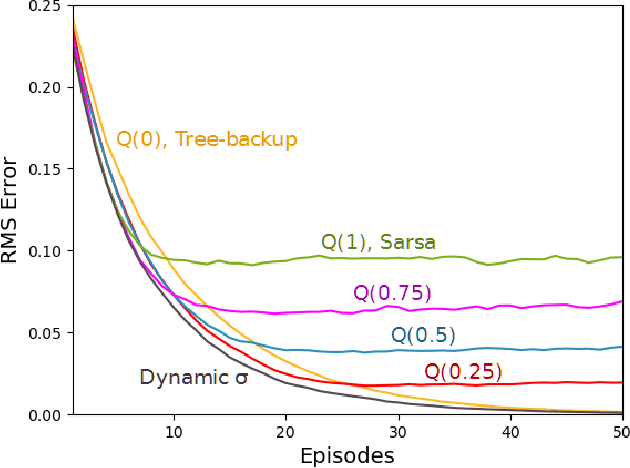
Abstract:Unifying seemingly disparate algorithmic ideas to produce better performing algorithms has been a longstanding goal in reinforcement learning. As a primary example, TD($\lambda$) elegantly unifies one-step TD prediction with Monte Carlo methods through the use of eligibility traces and the trace-decay parameter $\lambda$. Currently, there are a multitude of algorithms that can be used to perform TD control, including Sarsa, $Q$-learning, and Expected Sarsa. These methods are often studied in the one-step case, but they can be extended across multiple time steps to achieve better performance. Each of these algorithms is seemingly distinct, and no one dominates the others for all problems. In this paper, we study a new multi-step action-value algorithm called $Q(\sigma)$ which unifies and generalizes these existing algorithms, while subsuming them as special cases. A new parameter, $\sigma$, is introduced to allow the degree of sampling performed by the algorithm at each step during its backup to be continuously varied, with Sarsa existing at one extreme (full sampling), and Expected Sarsa existing at the other (pure expectation). $Q(\sigma)$ is generally applicable to both on- and off-policy learning, but in this work we focus on experiments in the on-policy case. Our results show that an intermediate value of $\sigma$, which results in a mixture of the existing algorithms, performs better than either extreme. The mixture can also be varied dynamically which can result in even greater performance.
* Appeared at the Thirty-Second AAAI Conference on Artificial Intelligence (AAAI-18)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge