Back to Square One: Superhuman Performance in Chutes and Ladders Through Deep Neural Networks and Tree Search

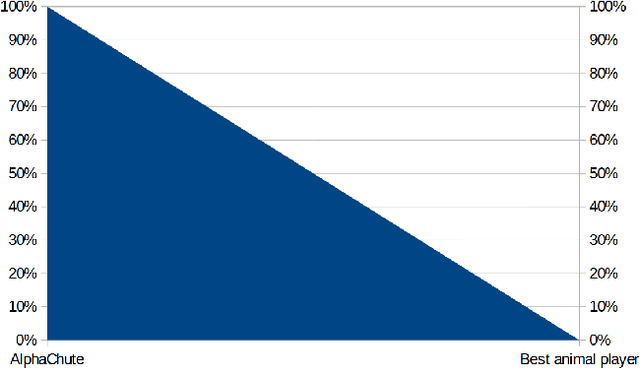
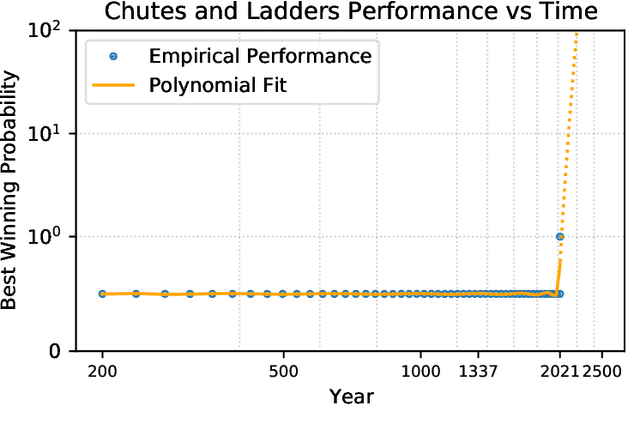
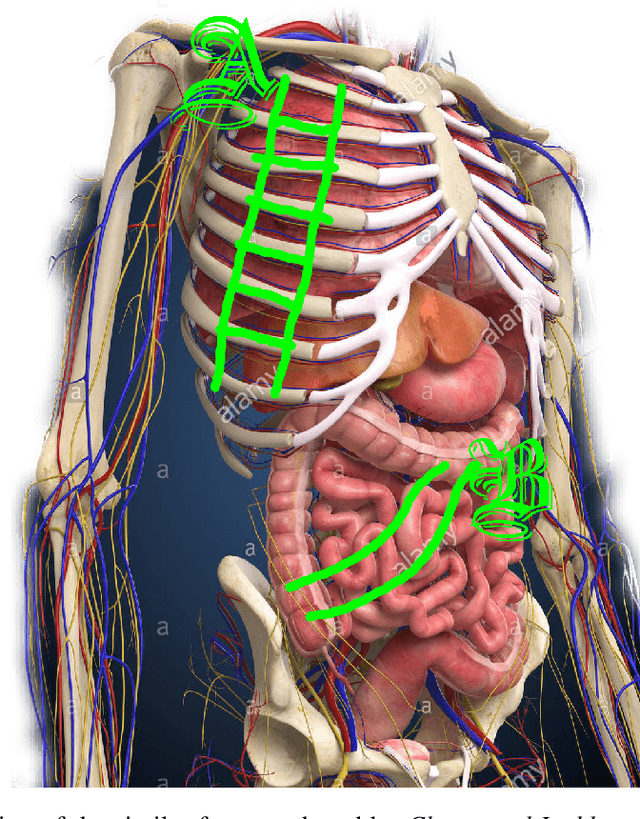
We present AlphaChute: a state-of-the-art algorithm that achieves superhuman performance in the ancient game of Chutes and Ladders. We prove that our algorithm converges to the Nash equilibrium in constant time, and therefore is -- to the best of our knowledge -- the first such formal solution to this game. Surprisingly, despite all this, our implementation of AlphaChute remains relatively straightforward due to domain-specific adaptations. We provide the source code for AlphaChute here in our Appendix.

Incrementally Learning Functions of the Return

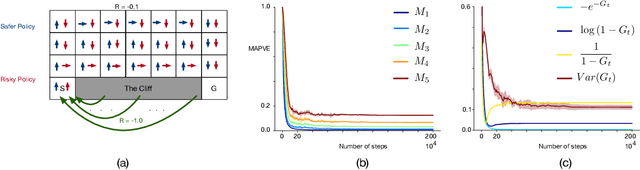
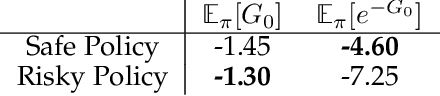
Temporal difference methods enable efficient estimation of value functions in reinforcement learning in an incremental fashion, and are of broader interest because they correspond learning as observed in biological systems. Standard value functions correspond to the expected value of a sum of discounted returns. While this formulation is often sufficient for many purposes, it would often be useful to be able to represent functions of the return as well. Unfortunately, most such functions cannot be estimated directly using TD methods. We propose a means of estimating functions of the return using its moments, which can be learned online using a modified TD algorithm. The moments of the return are then used as part of a Taylor expansion to approximate analytic functions of the return.

Predicting Periodicity with Temporal Difference Learning

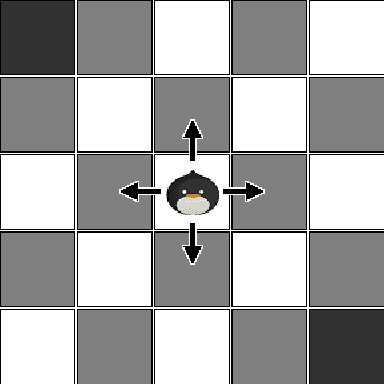
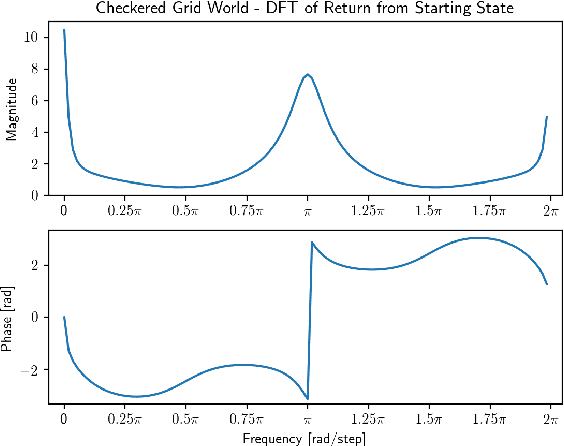
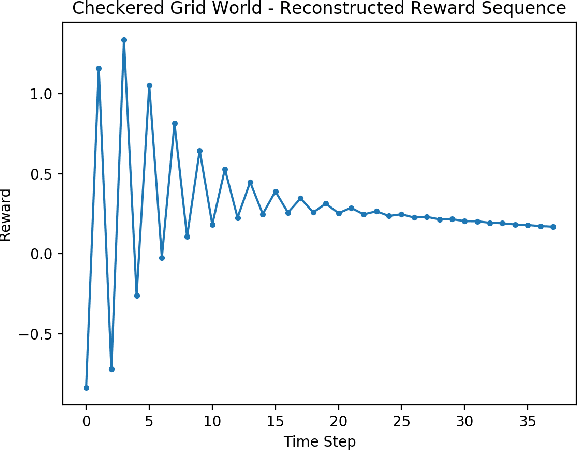
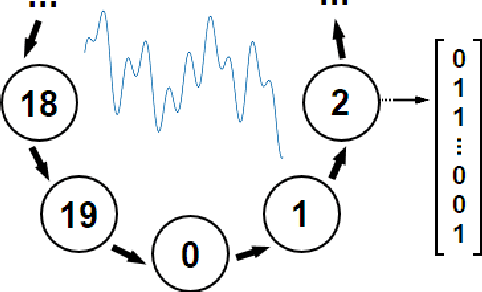
Temporal difference (TD) learning is an important approach in reinforcement learning, as it combines ideas from dynamic programming and Monte Carlo methods in a way that allows for online and incremental model-free learning. A key idea of TD learning is that it is learning predictive knowledge about the environment in the form of value functions, from which it can derive its behavior to address long-term sequential decision making problems. The agent's horizon of interest, that is, how immediate or long-term a TD learning agent predicts into the future, is adjusted through a discount rate parameter. In this paper, we introduce an alternative view on the discount rate, with insight from digital signal processing, to include complex-valued discounting. Our results show that setting the discount rate to appropriately chosen complex numbers allows for online and incremental estimation of the Discrete Fourier Transform (DFT) of a signal of interest with TD learning. We thereby extend the types of knowledge representable by value functions, which we show are particularly useful for identifying periodic effects in the reward sequence.

Directly Estimating the Variance of the λ-Return Using Temporal-Difference Methods

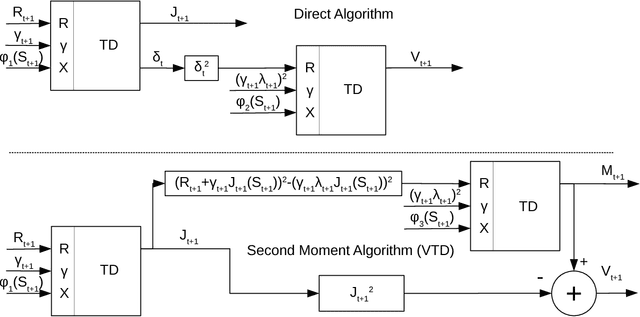
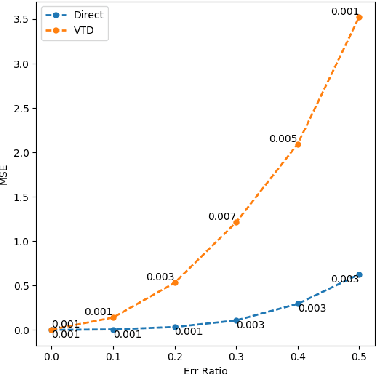
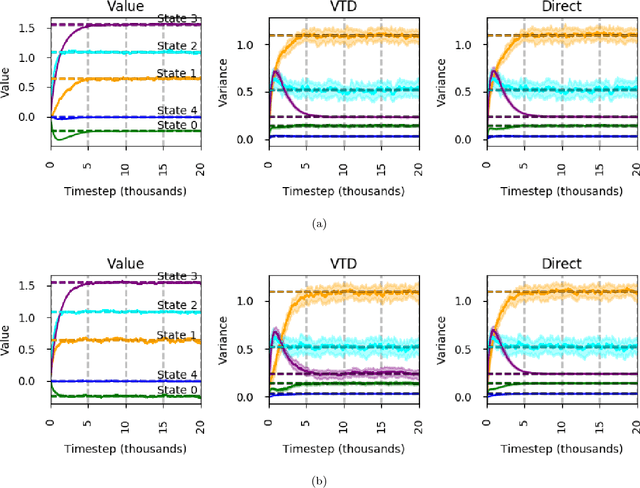
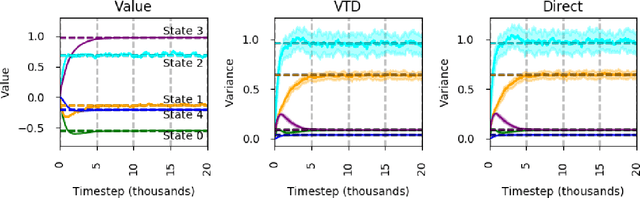
This paper investigates estimating the variance of a temporal-difference learning agent's update target. Most reinforcement learning methods use an estimate of the value function, which captures how good it is for the agent to be in a particular state and is mathematically expressed as the expected sum of discounted future rewards (called the return). These values can be straightforwardly estimated by averaging batches of returns using Monte Carlo methods. However, if we wish to update the agent's value estimates during learning--before terminal outcomes are observed--we must use a different estimation target called the {\lambda}-return, which truncates the return with the agent's own estimate of the value function. Temporal difference learning methods estimate the expected {\lambda}-return for each state, allowing these methods to update online and incrementally, and in most cases achieve better generalization error and faster learning than Monte Carlo methods. Naturally one could attempt to estimate higher-order moments of the {\lambda}-return. This paper is about estimating the variance of the {\lambda}-return. Prior work has shown that given estimates of the variance of the {\lambda}-return, learning systems can be constructed to (1) mitigate risk in action selection, and (2) automatically adapt the parameters of the learning process itself to improve performance. Unfortunately, existing methods for estimating the variance of the {\lambda}-return are complex and not well understood empirically. We contribute a method for estimating the variance of the {\lambda}-return directly using policy evaluation methods from reinforcement learning. Our approach is significantly simpler than prior methods that independently estimate the second moment of the {\lambda}-return. Empirically our new approach behaves at least as well as existing approaches, but is generally more robust.