Preserving Plasticity in Continual Learning with Adaptive Linearity Injection

Loss of plasticity in deep neural networks is the gradual reduction in a model's capacity to incrementally learn and has been identified as a key obstacle to learning in non-stationary problem settings. Recent work has shown that deep linear networks tend to be resilient towards loss of plasticity. Motivated by this observation, we propose Adaptive Linearization (AdaLin), a general approach that dynamically adapts each neuron's activation function to mitigate plasticity loss. Unlike prior methods that rely on regularization or periodic resets, AdaLin equips every neuron with a learnable parameter and a gating mechanism that injects linearity into the activation function based on its gradient flow. This adaptive modulation ensures sufficient gradient signal and sustains continual learning without introducing additional hyperparameters or requiring explicit task boundaries. When used with conventional activation functions like ReLU, Tanh, and GeLU, we demonstrate that AdaLin can significantly improve performance on standard benchmarks, including Random Label and Permuted MNIST, Random Label and Shuffled CIFAR-10, and Class-Split CIFAR-100. Furthermore, its efficacy is shown in more complex scenarios, such as class-incremental learning on CIFAR-100 with a ResNet-18 backbone, and in mitigating plasticity loss in off-policy reinforcement learning agents. We perform a systematic set of ablations that show that neuron-level adaptation is crucial for good performance and analyze a number of metrics in the network that might be correlated to loss of plasticity.

Parseval Regularization for Continual Reinforcement Learning

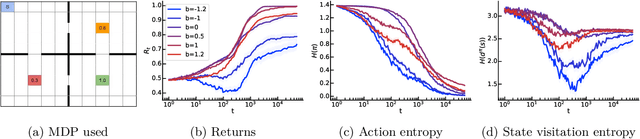
Loss of plasticity, trainability loss, and primacy bias have been identified as issues arising when training deep neural networks on sequences of tasks -- all referring to the increased difficulty in training on new tasks. We propose to use Parseval regularization, which maintains orthogonality of weight matrices, to preserve useful optimization properties and improve training in a continual reinforcement learning setting. We show that it provides significant benefits to RL agents on a suite of gridworld, CARL and MetaWorld tasks. We conduct comprehensive ablations to identify the source of its benefits and investigate the effect of certain metrics associated to network trainability including weight matrix rank, weight norms and policy entropy.

The Role of Baselines in Policy Gradient Optimization

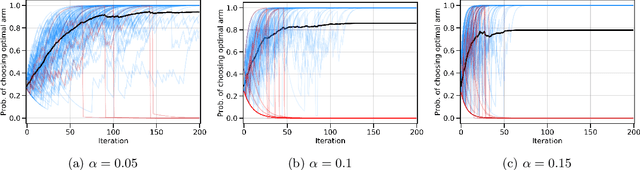
We study the effect of baselines in on-policy stochastic policy gradient optimization, and close the gap between the theory and practice of policy optimization methods. Our first contribution is to show that the \emph{state value} baseline allows on-policy stochastic \emph{natural} policy gradient (NPG) to converge to a globally optimal policy at an $O(1/t)$ rate, which was not previously known. The analysis relies on two novel findings: the expected progress of the NPG update satisfies a stochastic version of the non-uniform \L{}ojasiewicz (N\L{}) inequality, and with probability 1 the state value baseline prevents the optimal action's probability from vanishing, thus ensuring sufficient exploration. Importantly, these results provide a new understanding of the role of baselines in stochastic policy gradient: by showing that the variance of natural policy gradient estimates remains unbounded with or without a baseline, we find that variance reduction \emph{cannot} explain their utility in this setting. Instead, the analysis reveals that the primary effect of the value baseline is to \textbf{reduce the aggressiveness of the updates} rather than their variance. That is, we demonstrate that a finite variance is \emph{not necessary} for almost sure convergence of stochastic NPG, while controlling update aggressiveness is both necessary and sufficient. Additional experimental results verify these theoretical findings.

Beyond variance reduction: Understanding the true impact of baselines on policy optimization

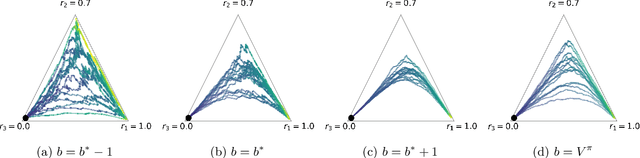
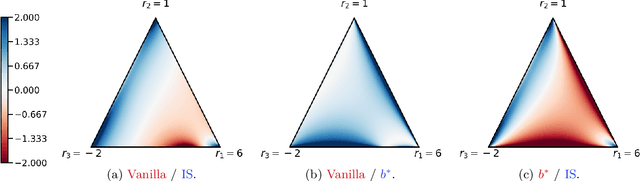
Policy gradients methods are a popular and effective choice to train reinforcement learning agents in complex environments. The variance of the stochastic policy gradient is often seen as a key quantity to determine the effectiveness of the algorithm. Baselines are a common addition to reduce the variance of the gradient, but previous works have hardly ever considered other effects baselines may have on the optimization process. Using simple examples, we find that baselines modify the optimization dynamics even when the variance is the same. In certain cases, a baseline with lower variance may even be worse than another with higher variance. Furthermore, we find that the choice of baseline can affect the convergence of natural policy gradient, where certain baselines may lead to convergence to a suboptimal policy for any stepsize. Such behaviour emerges when sampling is constrained to be done using the current policy and we show how decoupling the sampling policy from the current policy guarantees convergence for a much wider range of baselines. More broadly, this work suggests that a more careful treatment of stochasticity in the updates---beyond the immediate variance---is necessary to understand the optimization process of policy gradient algorithms.

Incrementally Learning Functions of the Return

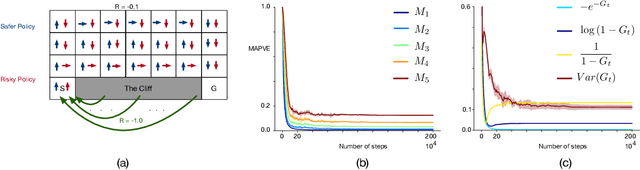
Temporal difference methods enable efficient estimation of value functions in reinforcement learning in an incremental fashion, and are of broader interest because they correspond learning as observed in biological systems. Standard value functions correspond to the expected value of a sum of discounted returns. While this formulation is often sufficient for many purposes, it would often be useful to be able to represent functions of the return as well. Unfortunately, most such functions cannot be estimated directly using TD methods. We propose a means of estimating functions of the return using its moments, which can be learned online using a modified TD algorithm. The moments of the return are then used as part of a Taylor expansion to approximate analytic functions of the return.

Importance Resampling for Off-policy Prediction

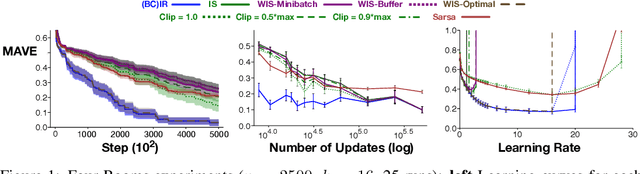
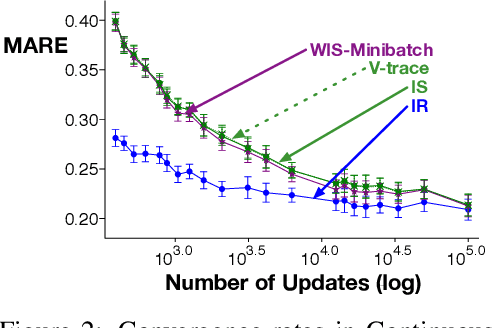
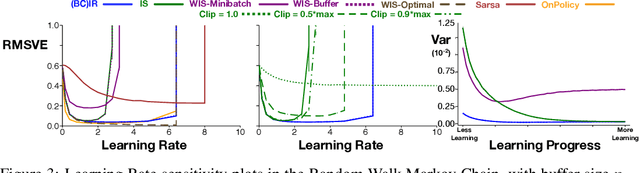
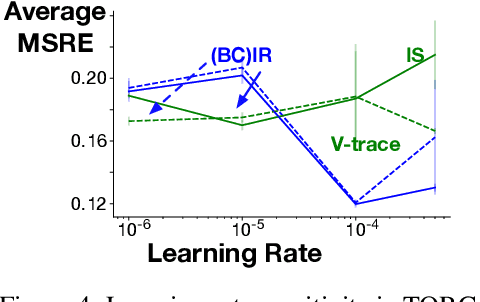
Importance sampling (IS) is a common reweighting strategy for off-policy prediction in reinforcement learning. While it is consistent and unbiased, it can result in high variance updates to the weights for the value function. In this work, we explore a resampling strategy as an alternative to reweighting. We propose Importance Resampling (IR) for off-policy prediction, which resamples experience from a replay buffer and applies standard on-policy updates. The approach avoids using importance sampling ratios in the update, instead correcting the distribution before the update. We characterize the bias and consistency of IR, particularly compared to Weighted IS (WIS). We demonstrate in several microworlds that IR has improved sample efficiency and lower variance updates, as compared to IS and several variance-reduced IS strategies, including variants of WIS and V-trace which clips IS ratios. We also provide a demonstration showing IR improves over IS for learning a value function from images in a racing car simulator.

High-confidence error estimates for learned value functions

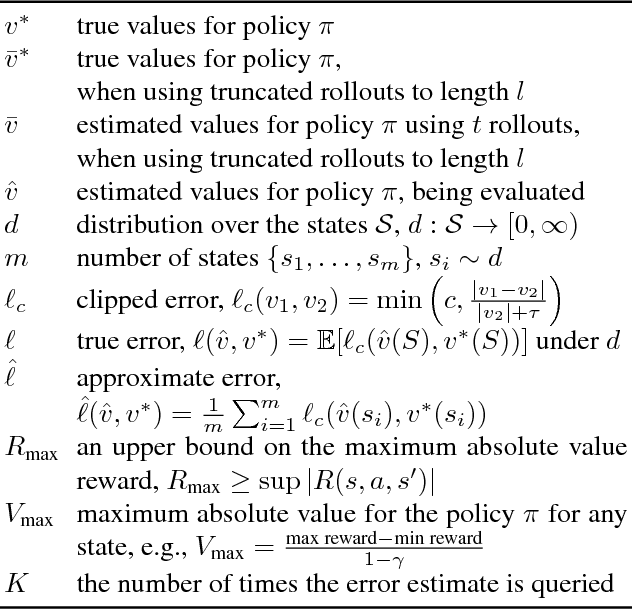
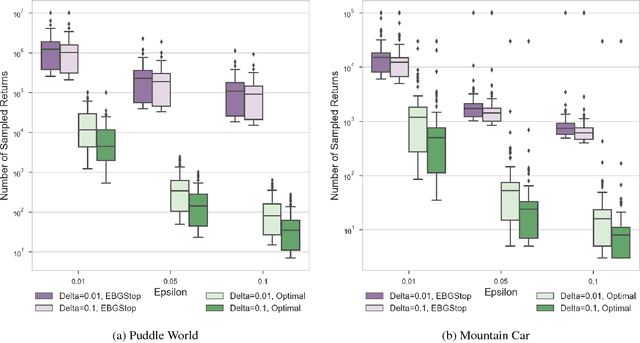
Estimating the value function for a fixed policy is a fundamental problem in reinforcement learning. Policy evaluation algorithms---to estimate value functions---continue to be developed, to improve convergence rates, improve stability and handle variability, particularly for off-policy learning. To understand the properties of these algorithms, the experimenter needs high-confidence estimates of the accuracy of the learned value functions. For environments with small, finite state-spaces, like chains, the true value function can be easily computed, to compute accuracy. For large, or continuous state-spaces, however, this is no longer feasible. In this paper, we address the largely open problem of how to obtain these high-confidence estimates, for general state-spaces. We provide a high-confidence bound on an empirical estimate of the value error to the true value error. We use this bound to design an offline sampling algorithm, which stores the required quantities to repeatedly compute value error estimates for any learned value function. We provide experiments investigating the number of samples required by this offline algorithm in simple benchmark reinforcement learning domains, and highlight that there are still many open questions to be solved for this important problem.