RECipe: Does a Multi-Modal Recipe Knowledge Graph Fit a Multi-Purpose Recommendation System?

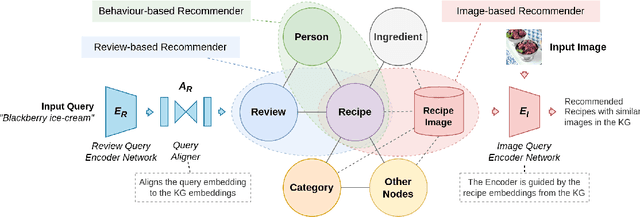
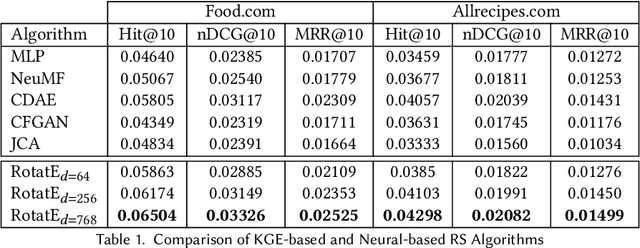
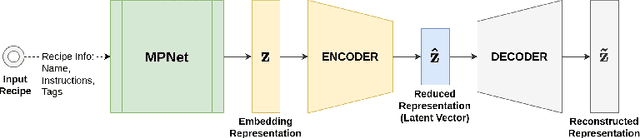
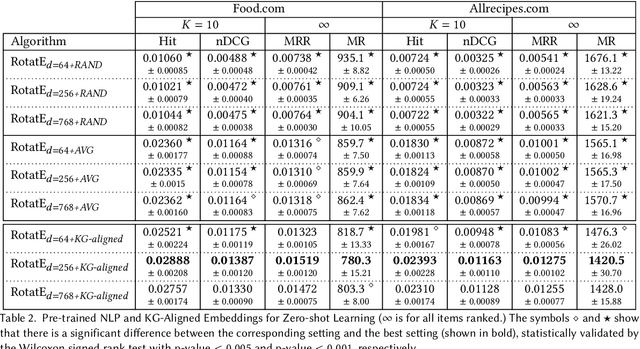
Over the past two decades, recommendation systems (RSs) have used machine learning (ML) solutions to recommend items, e.g., movies, books, and restaurants, to clients of a business or an online platform. Recipe recommendation, however, has not yet received much attention compared to those applications. We introduce RECipe as a multi-purpose recipe recommendation framework with a multi-modal knowledge graph (MMKG) backbone. The motivation behind RECipe is to go beyond (deep) neural collaborative filtering (NCF) by recommending recipes to users when they query in natural language or by providing an image. RECipe consists of 3 subsystems: (1) behavior-based recommender, (2) review-based recommender, and (3) image-based recommender. Each subsystem relies on the embedding representations of entities and relations in the graph. We first obtain (pre-trained) embedding representations of textual entities, such as reviews or ingredients, from a fine-tuned model of Microsoft's MPNet. We initialize the weights of the entities with these embeddings to train our knowledge graph embedding (KGE) model. For the visual component, i.e., recipe images, we develop a KGE-Guided variational autoencoder (KG-VAE) to learn the distribution of images and their latent representations. Once KGE and KG-VAE models are fully trained, we use them as a multi-purpose recommendation framework. For benchmarking, we created two knowledge graphs (KGs) from public datasets on Kaggle for recipe recommendation. Our experiments show that the KGE models have comparable performance to the neural solutions. We also present pre-trained NLP embeddings to address important applications such as zero-shot inference for new users (or the cold start problem) and conditional recommendation with respect to recipe categories. We eventually demonstrate the application of RECipe in a multi-purpose recommendation setting.

Self-Supervised Contrastive BERT Fine-tuning for Fusion-based Reviewed-Item Retrieval

As natural language interfaces enable users to express increasingly complex natural language queries, there is a parallel explosion of user review content that can allow users to better find items such as restaurants, books, or movies that match these expressive queries. While Neural Information Retrieval (IR) methods have provided state-of-the-art results for matching queries to documents, they have not been extended to the task of Reviewed-Item Retrieval (RIR), where query-review scores must be aggregated (or fused) into item-level scores for ranking. In the absence of labeled RIR datasets, we extend Neural IR methodology to RIR by leveraging self-supervised methods for contrastive learning of BERT embeddings for both queries and reviews. Specifically, contrastive learning requires a choice of positive and negative samples, where the unique two-level structure of our item-review data combined with meta-data affords us a rich structure for the selection of these samples. For contrastive learning in a Late Fusion scenario, we investigate the use of positive review samples from the same item and/or with the same rating, selection of hard positive samples by choosing the least similar reviews from the same anchor item, and selection of hard negative samples by choosing the most similar reviews from different items. We also explore anchor sub-sampling and augmenting with meta-data. For a more end-to-end Early Fusion approach, we introduce contrastive item embedding learning to fuse reviews into single item embeddings. Experimental results show that Late Fusion contrastive learning for Neural RIR outperforms all other contrastive IR configurations, Neural IR, and sparse retrieval baselines, thus demonstrating the power of exploiting the two-level structure in Neural RIR approaches as well as the importance of preserving the nuance of individual review content via Late Fusion methods.

An Optimal Private Stochastic-MAB Algorithm Based on an Optimal Private Stopping Rule

We present a provably optimal differentially private algorithm for the stochastic multi-arm bandit problem, as opposed to the private analogue of the UCB-algorithm [Mishra and Thakurta, 2015; Tossou and Dimitrakakis, 2016] which doesn't meet the recently discovered lower-bound of $\Omega \left(\frac{K\log(T)}{\epsilon} \right)$ [Shariff and Sheffet, 2018]. Our construction is based on a different algorithm, Successive Elimination [Even-Dar et al. 2002], that repeatedly pulls all remaining arms until an arm is found to be suboptimal and is then eliminated. In order to devise a private analogue of Successive Elimination we visit the problem of private stopping rule, that takes as input a stream of i.i.d samples from an unknown distribution and returns a multiplicative $(1 \pm \alpha)$-approximation of the distribution's mean, and prove the optimality of our private stopping rule. We then present the private Successive Elimination algorithm which meets both the non-private lower bound [Lai and Robbins, 1985] and the above-mentioned private lower bound. We also compare empirically the performance of our algorithm with the private UCB algorithm.

High-confidence error estimates for learned value functions

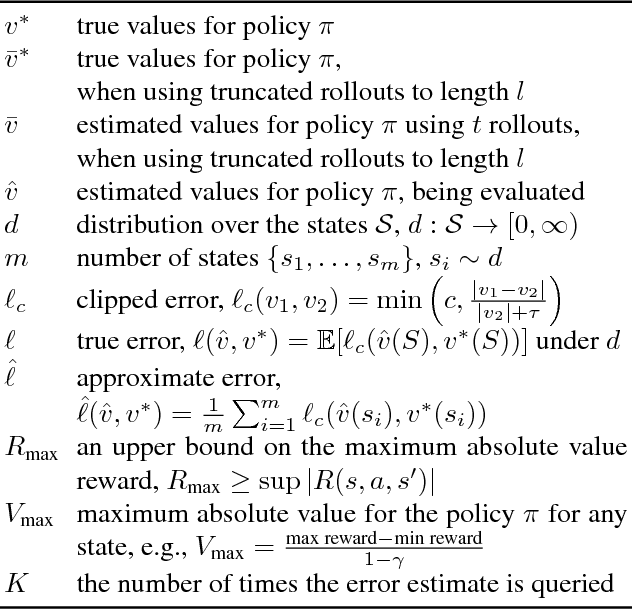
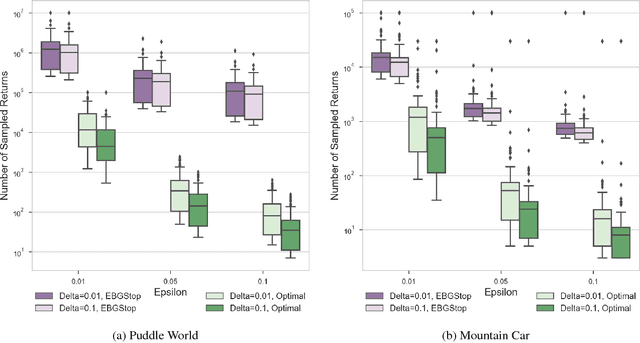
Estimating the value function for a fixed policy is a fundamental problem in reinforcement learning. Policy evaluation algorithms---to estimate value functions---continue to be developed, to improve convergence rates, improve stability and handle variability, particularly for off-policy learning. To understand the properties of these algorithms, the experimenter needs high-confidence estimates of the accuracy of the learned value functions. For environments with small, finite state-spaces, like chains, the true value function can be easily computed, to compute accuracy. For large, or continuous state-spaces, however, this is no longer feasible. In this paper, we address the largely open problem of how to obtain these high-confidence estimates, for general state-spaces. We provide a high-confidence bound on an empirical estimate of the value error to the true value error. We use this bound to design an offline sampling algorithm, which stores the required quantities to repeatedly compute value error estimates for any learned value function. We provide experiments investigating the number of samples required by this offline algorithm in simple benchmark reinforcement learning domains, and highlight that there are still many open questions to be solved for this important problem.