Privacy-Preserving Conformal Prediction Under Local Differential Privacy

Conformal prediction (CP) provides sets of candidate classes with a guaranteed probability of containing the true class. However, it typically relies on a calibration set with clean labels. We address privacy-sensitive scenarios where the aggregator is untrusted and can only access a perturbed version of the true labels. We propose two complementary approaches under local differential privacy (LDP). In the first approach, users do not access the model but instead provide their input features and a perturbed label using a k-ary randomized response. In the second approach, which enforces stricter privacy constraints, users add noise to their conformity score by binary search response. This method requires access to the classification model but preserves both data and label privacy. Both approaches compute the conformal threshold directly from noisy data without accessing the true labels. We prove finite-sample coverage guarantees and demonstrate robust coverage even under severe randomization. This approach unifies strong local privacy with predictive uncertainty control, making it well-suited for sensitive applications such as medical imaging or large language model queries, regardless of whether users can (or are willing to) compute their own scores.

A Private Approximation of the 2nd-Moment Matrix of Any Subsamplable Input

We study the problem of differentially private second moment estimation and present a new algorithm that achieve strong privacy-utility trade-offs even for worst-case inputs under subsamplability assumptions on the data. We call an input $(m,\alpha,\beta)$-subsamplable if a random subsample of size $m$ (or larger) preserves w.p $\geq 1-\beta$ the spectral structure of the original second moment matrix up to a multiplicative factor of $1\pm \alpha$. Building upon subsamplability, we give a recursive algorithmic framework similar to Kamath et al 2019, that abides zero-Concentrated Differential Privacy (zCDP) while preserving w.h.p. the accuracy of the second moment estimation upto an arbitrary factor of $(1\pm\gamma)$. We then show how to apply our algorithm to approximate the second moment matrix of a distribution $\mathcal{D}$, even when a noticeable fraction of the input are outliers.

Transfer Learning In Differential Privacy's Hybrid-Model

The hybrid-model (Avent et al 2017) in Differential Privacy is a an augmentation of the local-model where in addition to N local-agents we are assisted by one special agent who is in fact a curator holding the sensitive details of n additional individuals. Here we study the problem of machine learning in the hybrid-model where the n individuals in the curators dataset are drawn from a different distribution than the one of the general population (the local-agents). We give a general scheme -- Subsample-Test-Reweigh -- for this transfer learning problem, which reduces any curator-model DP-learner to a hybrid-model learner in this setting using iterative subsampling and reweighing of the n examples held by the curator based on a smooth variation of the Multiplicative-Weights algorithm (introduced by Bun et al, 2020). Our scheme has a sample complexity which relies on the chi-squared divergence between the two distributions. We give worst-case analysis bounds on the sample complexity required for our private reduction. Aiming to reduce said sample complexity, we give two specific instances our sample complexity can be drastically reduced (one instance is analyzed mathematically, while the other - empirically) and pose several directions for follow-up work.

Best-Arm Identification for Quantile Bandits with Privacy

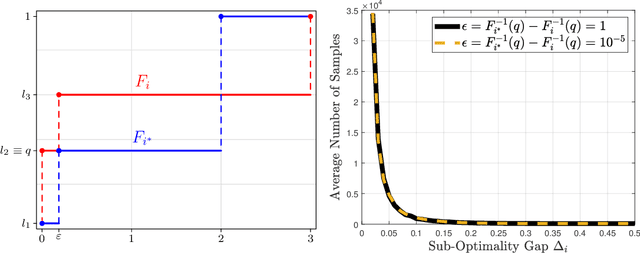
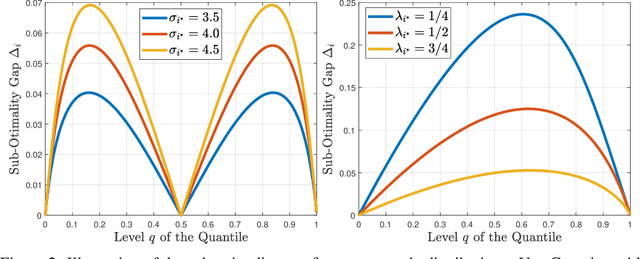
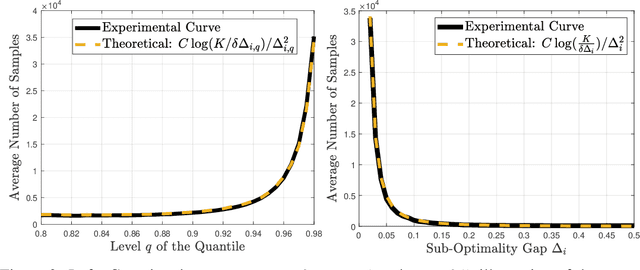
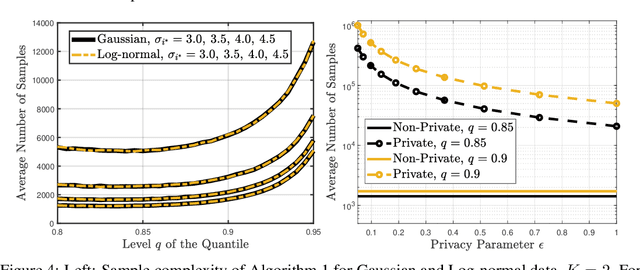
We study the best-arm identification problem in multi-armed bandits with stochastic, potentially private rewards, when the goal is to identify the arm with the highest quantile at a fixed, prescribed level. First, we propose a (non-private) successive elimination algorithm for strictly optimal best-arm identification, we show that our algorithm is $\delta$-PAC and we characterize its sample complexity. Further, we provide a lower bound on the expected number of pulls, showing that the proposed algorithm is essentially optimal up to logarithmic factors. Both upper and lower complexity bounds depend on a special definition of the associated suboptimality gap, designed in particular for the quantile bandit problem, as we show when the gap approaches zero, best-arm identification is impossible. Second, motivated by applications where the rewards are private, we provide a differentially private successive elimination algorithm whose sample complexity is finite even for distributions with infinite support-size, and we characterize its sample complexity as well. Our algorithms do not require prior knowledge of either the suboptimality gap or other statistical information related to the bandit problem at hand.

The power of synergy in differential privacy: Combining a small curator with local randomizers

Motivated by the desire to bridge the utility gap between local and trusted curator models of differential privacy for practical applications, we initiate the theoretical study of a hybrid model introduced by "Blender" [Avent et al.,\ USENIX Security '17], in which differentially private protocols of n agents that work in the local-model are assisted by a differentially private curator that has access to the data of m additional users. We focus on the regime where m << n and study the new capabilities of this (m,n)-hybrid model. We show that, despite the fact that the hybrid model adds no significant new capabilities for the basic task of simple hypothesis-testing, there are many other tasks (under a wide range of parameters) that can be solved in the hybrid model yet cannot be solved either by the curator or by the local-users separately. Moreover, we exhibit additional tasks where at least one round of interaction between the curator and the local-users is necessary -- namely, no hybrid model protocol without such interaction can solve these tasks. Taken together, our results show that the combination of the local model with a small curator can become part of a promising toolkit for designing and implementing differential privacy.

Differentially Private Algorithms for Learning Mixtures of Separated Gaussians

Learning the parameters of Gaussian mixture models is a fundamental and widely studied problem with numerous applications. In this work, we give new algorithms for learning the parameters of a high-dimensional, well separated, Gaussian mixture model subject to the strong constraint of differential privacy. In particular, we give a differentially private analogue of the algorithm of Achlioptas and McSherry. Our algorithm has two key properties not achieved by prior work: (1) The algorithm's sample complexity matches that of the corresponding non-private algorithm up to lower order terms in a wide range of parameters. (2) The algorithm does not require strong a priori bounds on the parameters of the mixture components.

An Optimal Private Stochastic-MAB Algorithm Based on an Optimal Private Stopping Rule

We present a provably optimal differentially private algorithm for the stochastic multi-arm bandit problem, as opposed to the private analogue of the UCB-algorithm [Mishra and Thakurta, 2015; Tossou and Dimitrakakis, 2016] which doesn't meet the recently discovered lower-bound of $\Omega \left(\frac{K\log(T)}{\epsilon} \right)$ [Shariff and Sheffet, 2018]. Our construction is based on a different algorithm, Successive Elimination [Even-Dar et al. 2002], that repeatedly pulls all remaining arms until an arm is found to be suboptimal and is then eliminated. In order to devise a private analogue of Successive Elimination we visit the problem of private stopping rule, that takes as input a stream of i.i.d samples from an unknown distribution and returns a multiplicative $(1 \pm \alpha)$-approximation of the distribution's mean, and prove the optimality of our private stopping rule. We then present the private Successive Elimination algorithm which meets both the non-private lower bound [Lai and Robbins, 1985] and the above-mentioned private lower bound. We also compare empirically the performance of our algorithm with the private UCB algorithm.

Differentially Private Contextual Linear Bandits

We study the contextual linear bandit problem, a version of the standard stochastic multi-armed bandit (MAB) problem where a learner sequentially selects actions to maximize a reward which depends also on a user provided per-round context. Though the context is chosen arbitrarily or adversarially, the reward is assumed to be a stochastic function of a feature vector that encodes the context and selected action. Our goal is to devise private learners for the contextual linear bandit problem. We first show that using the standard definition of differential privacy results in linear regret. So instead, we adopt the notion of joint differential privacy, where we assume that the action chosen on day $t$ is only revealed to user $t$ and thus needn't be kept private that day, only on following days. We give a general scheme converting the classic linear-UCB algorithm into a joint differentially private algorithm using the tree-based algorithm. We then apply either Gaussian noise or Wishart noise to achieve joint-differentially private algorithms and bound the resulting algorithms' regrets. In addition, we give the first lower bound on the additional regret any private algorithms for the MAB problem must incur.

Differentially Private Ordinary Least Squares

Linear regression is one of the most prevalent techniques in machine learning, however, it is also common to use linear regression for its \emph{explanatory} capabilities rather than label prediction. Ordinary Least Squares (OLS) is often used in statistics to establish a correlation between an attribute (e.g. gender) and a label (e.g. income) in the presence of other (potentially correlated) features. OLS assumes a particular model that randomly generates the data, and derives \emph{$t$-values} --- representing the likelihood of each real value to be the true correlation. Using $t$-values, OLS can release a \emph{confidence interval}, which is an interval on the reals that is likely to contain the true correlation, and when this interval does not intersect the origin, we can \emph{reject the null hypothesis} as it is likely that the true correlation is non-zero. Our work aims at achieving similar guarantees on data under differentially private estimators. First, we show that for well-spread data, the Gaussian Johnson-Lindenstrauss Transform (JLT) gives a very good approximation of $t$-values, secondly, when JLT approximates Ridge regression (linear regression with $l_2$-regularization) we derive, under certain conditions, confidence intervals using the projected data, lastly, we derive, under different conditions, confidence intervals for the "Analyze Gauss" algorithm (Dwork et al, STOC 2014).

Learning Mixtures of Ranking Models

This work concerns learning probabilistic models for ranking data in a heterogeneous population. The specific problem we study is learning the parameters of a Mallows Mixture Model. Despite being widely studied, current heuristics for this problem do not have theoretical guarantees and can get stuck in bad local optima. We present the first polynomial time algorithm which provably learns the parameters of a mixture of two Mallows models. A key component of our algorithm is a novel use of tensor decomposition techniques to learn the top-k prefix in both the rankings. Before this work, even the question of identifiability in the case of a mixture of two Mallows models was unresolved.