Distributionally Robust Power Policies for Wireless Systems under Power Fluctuation Risk

Modern wireless communication systems necessitate the development of cost-effective resource allocation strategies, while ensuring maximal system performance. While commonly realizable via efficient waterfilling schemes, ergodic-optimal policies often exhibit instantaneous resource constraint fluctuations as a result of fading variability, violating prescribed specifications possibly within unacceptable margins, inducing further operational challenges and/or costs. On the other extent, short-term-optimal policies -- commonly based on deterministic waterfilling-- while strictly maintaining operational specifications, are not only impractical and computationally demanding, but also suboptimal in a long-term sense. To address these challenges, we introduce a novel distributionally robust version of a classical point-to-point interference-free multi-terminal constrained stochastic resource allocation problem, by leveraging the Conditional Value-at-Risk (CVaR) as a coherent measure of power policy fluctuation risk. We derive closed-form dual-parameterized expressions for the CVaR-optimal resource policy, along with corresponding optimal CVaR quantile levels by capitalizing on (sampling) the underlying fading distribution. We subsequently develop two dual-domain schemes -- one model-based and one model-free -- to iteratively determine a globally-optimal resource policy. Our numerical simulations confirm the remarkable effectiveness of the proposed approach, also revealing an almost-constant character of the CVaR-optimal policy and at rather minimal ergodic rate optimality loss.

Stochastic Resource Allocation via Dual Tail Waterfilling

Optimal resource allocation in wireless systems still stands as a rather challenging task due to the inherent statistical characteristics of channel fading. On the one hand, minimax/outage-optimal policies are often overconservative and analytically intractable, despite advertising maximally reliable system performance. On the other hand, ergodic-optimal resource allocation policies are often susceptible to the statistical dispersion of heavy-tailed fading channels, leading to relatively frequent drastic performance drops. We investigate a new risk-aware formulation of the classical stochastic resource allocation problem for point-to-point power-constrained communication networks over fading channels with no cross-interference, by leveraging the Conditional Value-at-Risk (CV@R) as a coherent measure of risk. We rigorously derive closed-form expressions for the CV@R-optimal risk-aware resource allocation policy, as well as the optimal associated quantiles of the corresponding user rate functions by capitalizing on the underlying fading distribution, parameterized by dual variables. We then develop a purely dual tail waterfilling scheme, achieving significantly more rapid and assured convergence of dual variables, as compared with the primal-dual tail waterfilling algorithm, recently proposed in the literature. The effectiveness of the proposed scheme is also readily confirmed via detailed numerical simulations.

Robust and Reliable Stochastic Resource Allocation via Tail Waterfilling

Stochastic allocation of resources in the context of wireless systems ultimately demands reactive decision making for meaningfully optimizing network-wide random utilities, while respecting certain resource constraints. Standard ergodic-optimal policies are however susceptible to the statistical variability of fading, often leading to systems which are severely unreliable and spectrally wasteful. On the flip side, minimax/outage-optimal policies are too pessimistic and often hard to determine. We propose a new risk-aware formulation of the resource allocation problem for standard multi-user point-to-point power-constrained communication with no cross-interference, by employing the Conditional Value-at-Risk (CV@R) as a measure of fading risk. A remarkable feature of this approach is that it is a convex generalization of the ergodic setting while inducing robustness and reliability in a fully tunable way, thus bridging the gap between the (naive) ergodic and (conservative) minimax approaches. We provide a closed-form expression for the CV@R-optimal policy given primal/dual variables, extending the classical stochastic waterfilling policy. We then develop a primal-dual tail-waterfilling scheme to recursively learn a globally optimal risk-aware policy. The effectiveness of the approach is verified via detailed simulations.

Beyond Lipschitz: Sharp Generalization and Excess Risk Bounds for Full-Batch GD

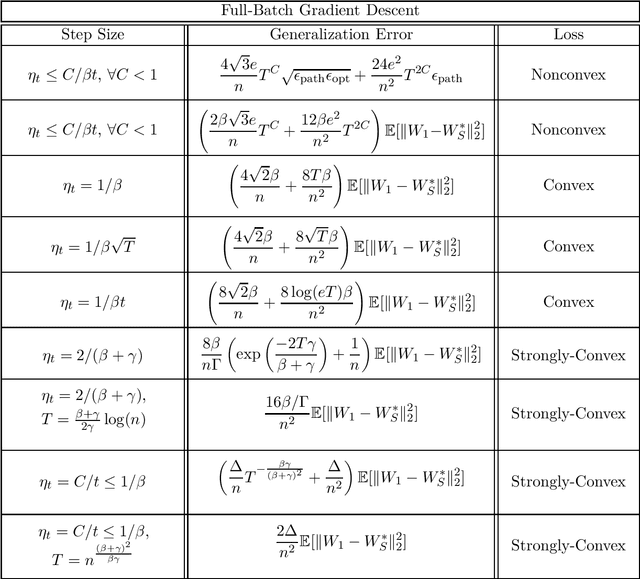
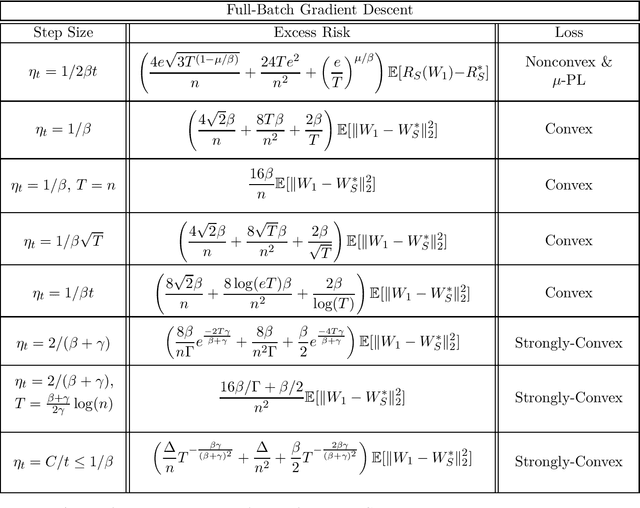
We provide sharp path-dependent generalization and excess error guarantees for the full-batch Gradient Decent (GD) algorithm for smooth losses (possibly non-Lipschitz, possibly nonconvex). At the heart of our analysis is a novel generalization error technique for deterministic symmetric algorithms, that implies average output stability and a bounded expected gradient of the loss at termination leads to generalization. This key result shows that small generalization error occurs at stationary points, and allows us to bypass Lipschitz assumptions on the loss prevalent in previous work. For nonconvex, convex and strongly convex losses, we show the explicit dependence of the generalization error in terms of the accumulated path-dependent optimization error, terminal optimization error, number of samples, and number of iterations. For nonconvex smooth losses, we prove that full-batch GD efficiently generalizes close to any stationary point at termination, under the proper choice of a decreasing step size. Further, if the loss is nonconvex but the objective is PL, we derive vanishing bounds on the corresponding excess risk. For convex and strongly-convex smooth losses, we prove that full-batch GD generalizes even for large constant step sizes, and achieves a small excess risk while training fast. Our full-batch GD generalization error and excess risk bounds are significantly tighter than the existing bounds for (stochastic) GD, when the loss is smooth (but possibly non-Lipschitz).

Black-Box Generalization

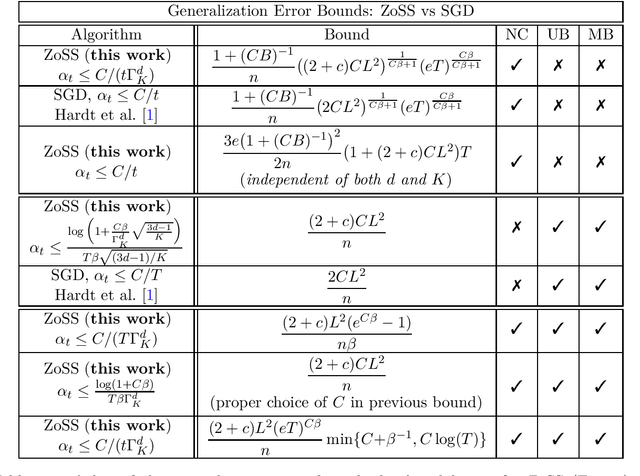
We provide the first generalization error analysis for black-box learning through derivative-free optimization. Under the assumption of a Lipschitz and smooth unknown loss, we consider the Zeroth-order Stochastic Search (ZoSS) algorithm, that updates a $d$-dimensional model by replacing stochastic gradient directions with stochastic differences of $K+1$ perturbed loss evaluations per dataset (example) query. For both unbounded and bounded possibly nonconvex losses, we present the first generalization bounds for the ZoSS algorithm. These bounds coincide with those for SGD, and rather surprisingly are independent of $d$, $K$ and the batch size $m$, under appropriate choices of a slightly decreased learning rate. For bounded nonconvex losses and a batch size $m=1$, we additionally show that both generalization error and learning rate are independent of $d$ and $K$, and remain essentially the same as for the SGD, even for two function evaluations. Our results extensively extend and consistently recover established results for SGD in prior work, on both generalization bounds and corresponding learning rates. If additionally $m=n$, where $n$ is the dataset size, we derive generalization guarantees for full-batch GD as well.

Model-Free Learning of Optimal Deterministic Resource Allocations in Wireless Systems via Action-Space Exploration

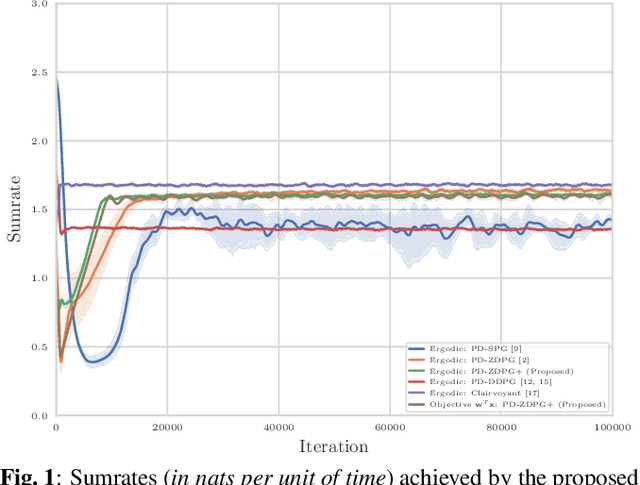
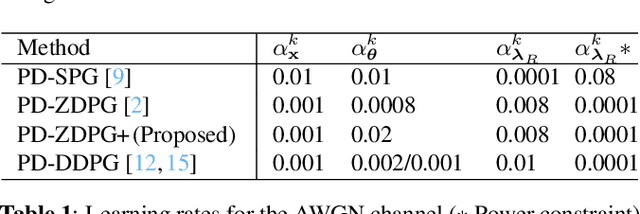
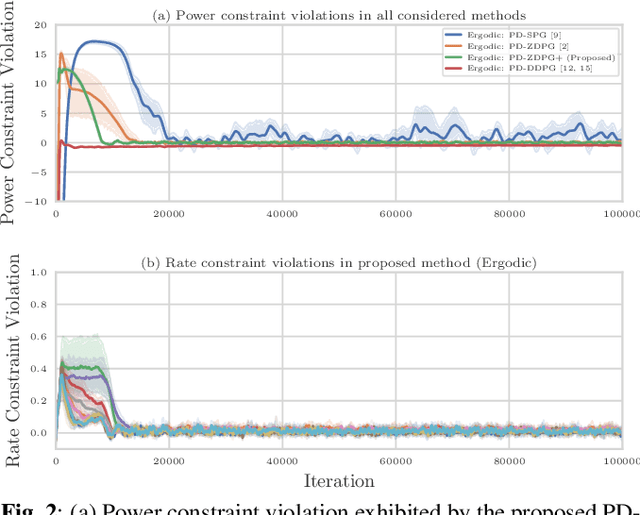
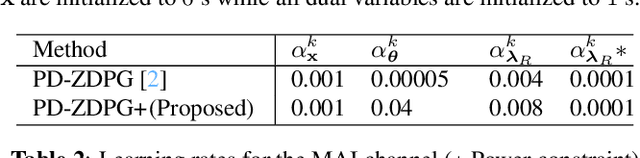
Wireless systems resource allocation refers to perpetual and challenging nonconvex constrained optimization tasks, which are especially timely in modern communications and networking setups involving multiple users with heterogeneous objectives and imprecise or even unknown models and/or channel statistics. In this paper, we propose a technically grounded and scalable primal-dual deterministic policy gradient method for efficiently learning optimal parameterized resource allocation policies. Our method not only efficiently exploits gradient availability of popular universal policy representations, such as deep neural networks, but is also truly model-free, as it relies on consistent zeroth-order gradient approximations of the associated random network services constructed via low-dimensional perturbations in action space, thus fully bypassing any dependence on critics. Both theory and numerical simulations confirm the efficacy and applicability of the proposed approach, as well as its superiority over the current state of the art in terms of both achieving near-optimal performance and scalability.

Uncertainty Principles in Risk-Aware Statistical Estimation

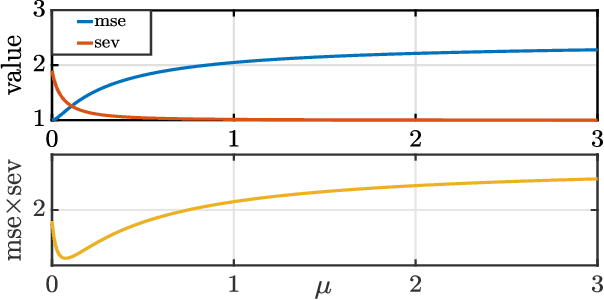
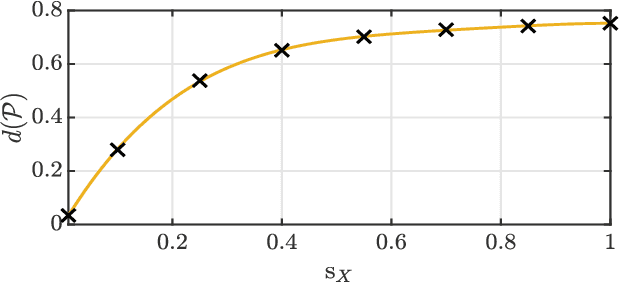
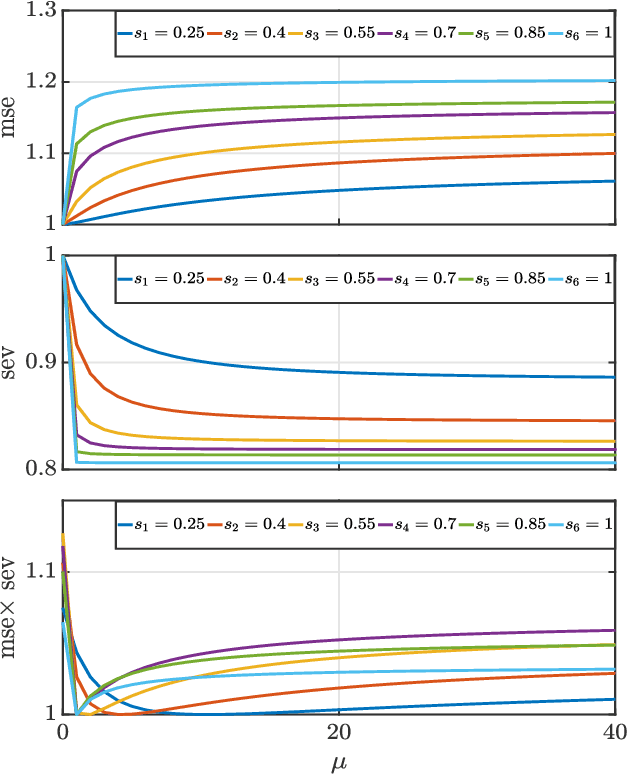
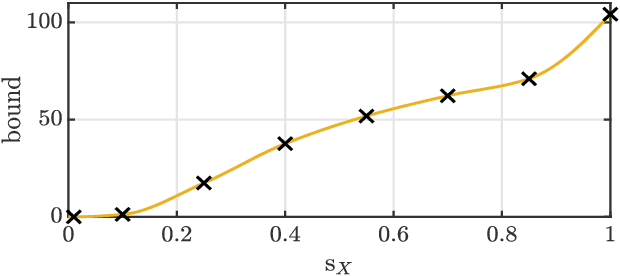
We present a new uncertainty principle for risk-aware statistical estimation, effectively quantifying the inherent trade-off between mean squared error ($\mse$) and risk, the latter measured by the associated average predictive squared error variance ($\sev$), for every admissible estimator of choice. Our uncertainty principle has a familiar form and resembles fundamental and classical results arising in several other areas, such as the Heisenberg principle in statistical and quantum mechanics, and the Gabor limit (time-scale trade-offs) in harmonic analysis. In particular, we prove that, provided a joint generative model of states and observables, the product between $\mse$ and $\sev$ is bounded from below by a computable model-dependent constant, which is explicitly related to the Pareto frontier of a recently studied $\sev$-constrained minimum $\mse$ (MMSE) estimation problem. Further, we show that the aforementioned constant is inherently connected to an intuitive new and rigorously topologically grounded statistical measure of distribution skewness in multiple dimensions, consistent with Pearson's moment coefficient of skewness for variables on the line. Our results are also illustrated via numerical simulations.

Noisy Linear Convergence of Stochastic Gradient Descent for CV@R Statistical Learning under Polyak-Łojasiewicz Conditions

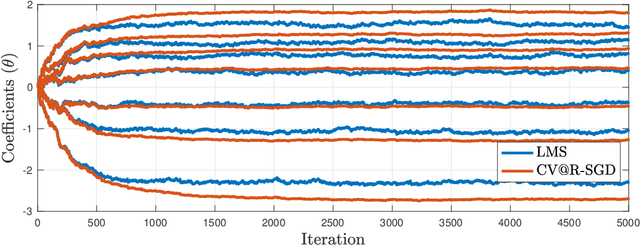
Conditional Value-at-Risk ($\mathrm{CV@R}$) is one of the most popular measures of risk, which has been recently considered as a performance criterion in supervised statistical learning, as it is related to desirable operational features in modern applications, such as safety, fairness, distributional robustness, and prediction error stability. However, due to its variational definition, $\mathrm{CV@R}$ is commonly believed to result in difficult optimization problems, even for smooth and strongly convex loss functions. We disprove this statement by establishing noisy (i.e., fixed-accuracy) linear convergence of stochastic gradient descent for sequential $\mathrm{CV@R}$ learning, for a large class of not necessarily strongly-convex (or even convex) loss functions satisfying a set-restricted Polyak-Lojasiewicz inequality. This class contains all smooth and strongly convex losses, confirming that classical problems, such as linear least squares regression, can be solved efficiently under the $\mathrm{CV@R}$ criterion, just as their risk-neutral versions. Our results are illustrated numerically on such a risk-aware ridge regression task, also verifying their validity in practice.

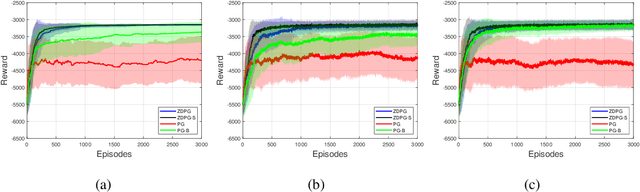
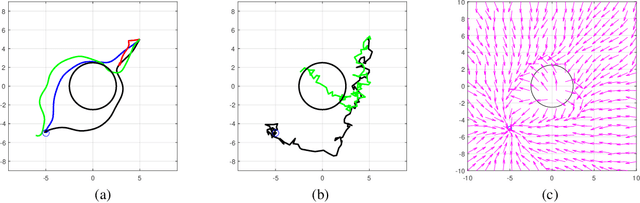
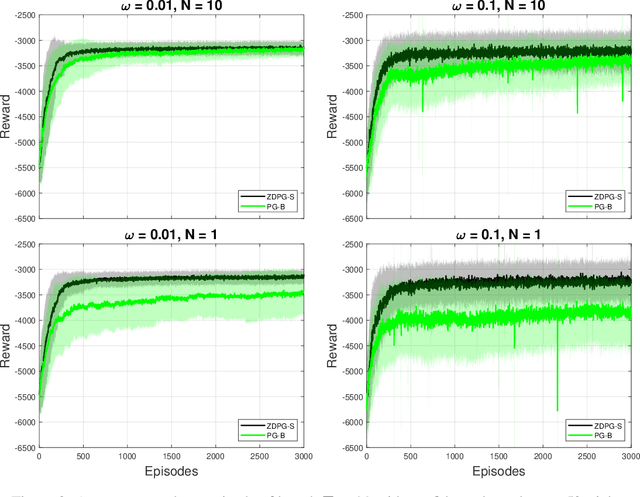
Zeroth-order Deterministic Policy Gradient

Deterministic Policy Gradient (DPG) removes a level of randomness from standard randomized-action Policy Gradient (PG), and demonstrates substantial empirical success for tackling complex dynamic problems involving Markov decision processes. At the same time, though, DPG loses its ability to learn in a model-free (i.e., actor-only) fashion, frequently necessitating the use of critics in order to obtain consistent estimates of the associated policy-reward gradient. In this work, we introduce Zeroth-order Deterministic Policy Gradient (ZDPG), which approximates policy-reward gradients via two-point stochastic evaluations of the $Q$-function, constructed by properly designed low-dimensional action-space perturbations. Exploiting the idea of random horizon rollouts for obtaining unbiased estimates of the $Q$-function, ZDPG lifts the dependence on critics and restores true model-free policy learning, while enjoying built-in and provable algorithmic stability. Additionally, we present new finite sample complexity bounds for ZDPG, which improve upon existing results by up to two orders of magnitude. Our findings are supported by several numerical experiments, which showcase the effectiveness of ZDPG in a practical setting, and its advantages over both PG and Baseline PG.

Best-Arm Identification for Quantile Bandits with Privacy

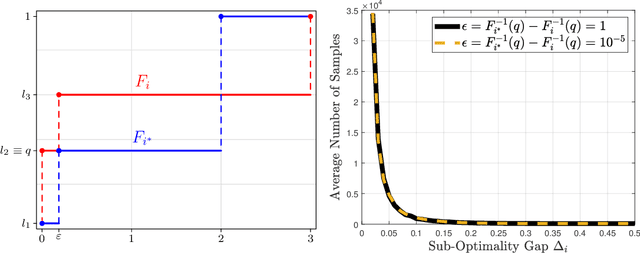
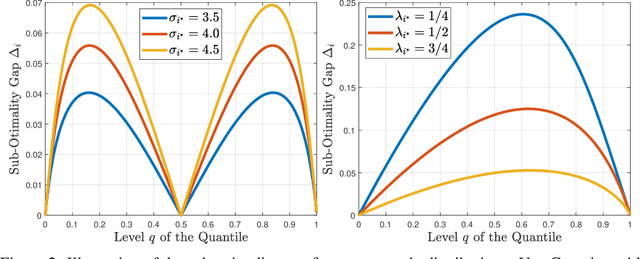
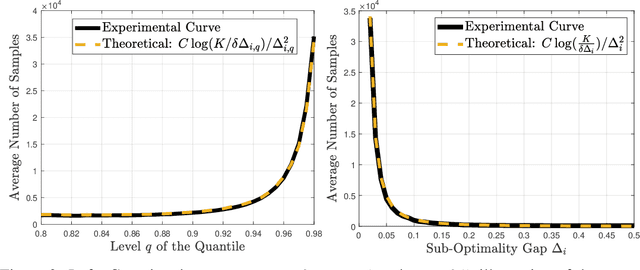
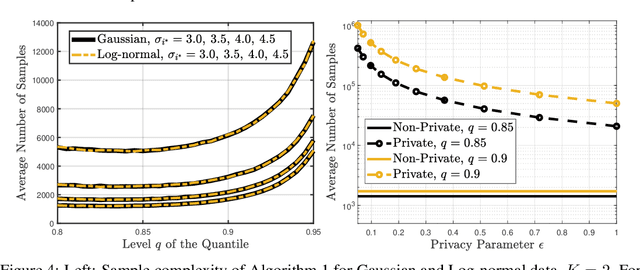
We study the best-arm identification problem in multi-armed bandits with stochastic, potentially private rewards, when the goal is to identify the arm with the highest quantile at a fixed, prescribed level. First, we propose a (non-private) successive elimination algorithm for strictly optimal best-arm identification, we show that our algorithm is $\delta$-PAC and we characterize its sample complexity. Further, we provide a lower bound on the expected number of pulls, showing that the proposed algorithm is essentially optimal up to logarithmic factors. Both upper and lower complexity bounds depend on a special definition of the associated suboptimality gap, designed in particular for the quantile bandit problem, as we show when the gap approaches zero, best-arm identification is impossible. Second, motivated by applications where the rewards are private, we provide a differentially private successive elimination algorithm whose sample complexity is finite even for distributions with infinite support-size, and we characterize its sample complexity as well. Our algorithms do not require prior knowledge of either the suboptimality gap or other statistical information related to the bandit problem at hand.