Noisy Linear Convergence of Stochastic Gradient Descent for CV@R Statistical Learning under Polyak-Łojasiewicz Conditions
Paper and Code
Jan 19, 2021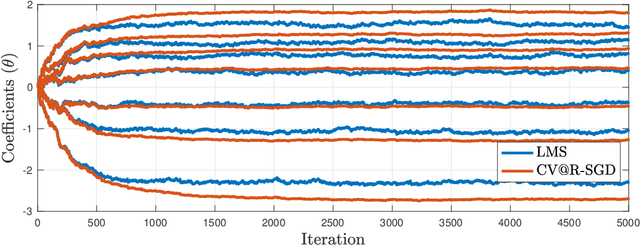

Conditional Value-at-Risk ($\mathrm{CV@R}$) is one of the most popular measures of risk, which has been recently considered as a performance criterion in supervised statistical learning, as it is related to desirable operational features in modern applications, such as safety, fairness, distributional robustness, and prediction error stability. However, due to its variational definition, $\mathrm{CV@R}$ is commonly believed to result in difficult optimization problems, even for smooth and strongly convex loss functions. We disprove this statement by establishing noisy (i.e., fixed-accuracy) linear convergence of stochastic gradient descent for sequential $\mathrm{CV@R}$ learning, for a large class of not necessarily strongly-convex (or even convex) loss functions satisfying a set-restricted Polyak-Lojasiewicz inequality. This class contains all smooth and strongly convex losses, confirming that classical problems, such as linear least squares regression, can be solved efficiently under the $\mathrm{CV@R}$ criterion, just as their risk-neutral versions. Our results are illustrated numerically on such a risk-aware ridge regression task, also verifying their validity in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge