Beyond Lipschitz: Sharp Generalization and Excess Risk Bounds for Full-Batch GD

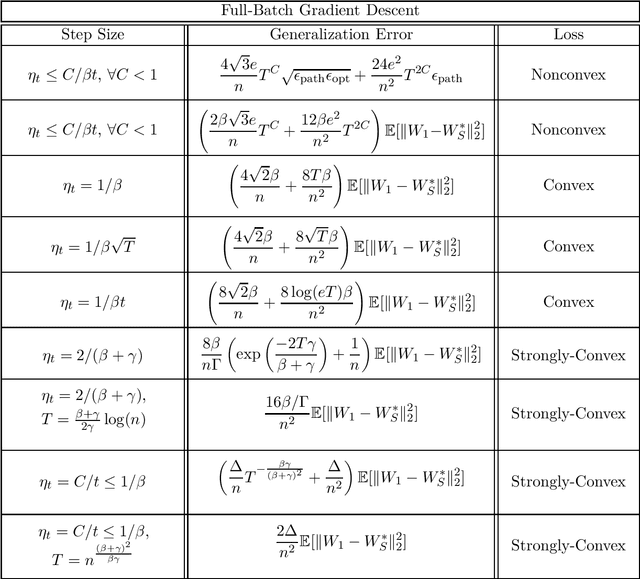
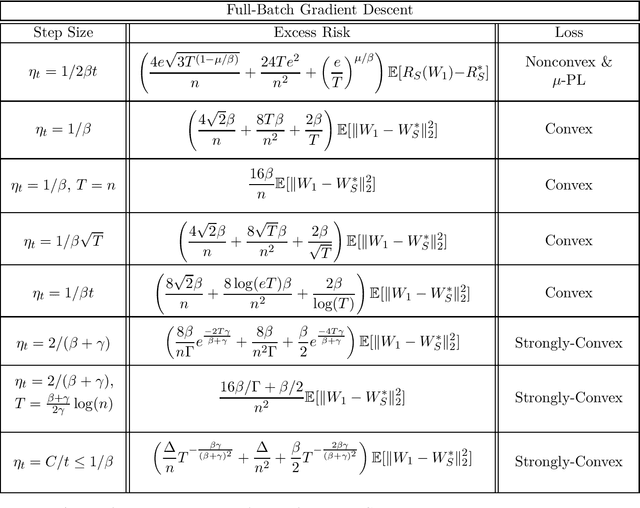
We provide sharp path-dependent generalization and excess error guarantees for the full-batch Gradient Decent (GD) algorithm for smooth losses (possibly non-Lipschitz, possibly nonconvex). At the heart of our analysis is a novel generalization error technique for deterministic symmetric algorithms, that implies average output stability and a bounded expected gradient of the loss at termination leads to generalization. This key result shows that small generalization error occurs at stationary points, and allows us to bypass Lipschitz assumptions on the loss prevalent in previous work. For nonconvex, convex and strongly convex losses, we show the explicit dependence of the generalization error in terms of the accumulated path-dependent optimization error, terminal optimization error, number of samples, and number of iterations. For nonconvex smooth losses, we prove that full-batch GD efficiently generalizes close to any stationary point at termination, under the proper choice of a decreasing step size. Further, if the loss is nonconvex but the objective is PL, we derive vanishing bounds on the corresponding excess risk. For convex and strongly-convex smooth losses, we prove that full-batch GD generalizes even for large constant step sizes, and achieves a small excess risk while training fast. Our full-batch GD generalization error and excess risk bounds are significantly tighter than the existing bounds for (stochastic) GD, when the loss is smooth (but possibly non-Lipschitz).

Learning Distributionally Robust Models at Scale via Composite Optimization

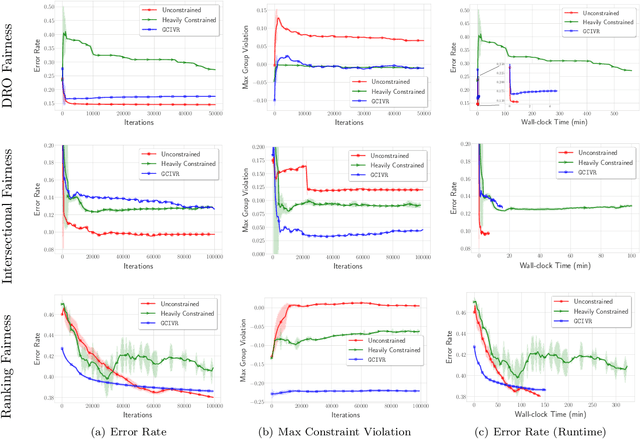
To train machine learning models that are robust to distribution shifts in the data, distributionally robust optimization (DRO) has been proven very effective. However, the existing approaches to learning a distributionally robust model either require solving complex optimization problems such as semidefinite programming or a first-order method whose convergence scales linearly with the number of data samples -- which hinders their scalability to large datasets. In this paper, we show how different variants of DRO are simply instances of a finite-sum composite optimization for which we provide scalable methods. We also provide empirical results that demonstrate the effectiveness of our proposed algorithm with respect to the prior art in order to learn robust models from very large datasets.

Black-Box Generalization

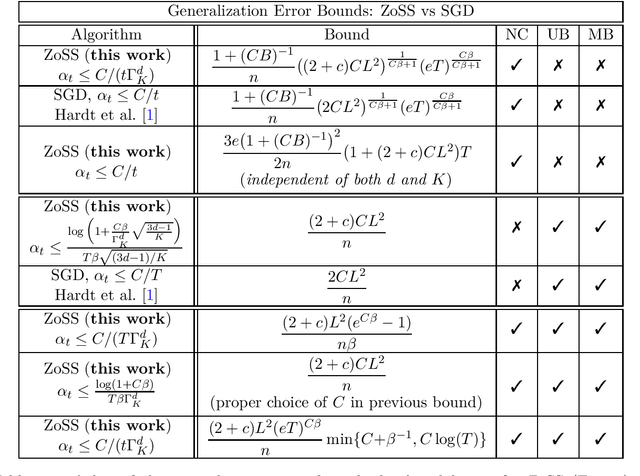
We provide the first generalization error analysis for black-box learning through derivative-free optimization. Under the assumption of a Lipschitz and smooth unknown loss, we consider the Zeroth-order Stochastic Search (ZoSS) algorithm, that updates a $d$-dimensional model by replacing stochastic gradient directions with stochastic differences of $K+1$ perturbed loss evaluations per dataset (example) query. For both unbounded and bounded possibly nonconvex losses, we present the first generalization bounds for the ZoSS algorithm. These bounds coincide with those for SGD, and rather surprisingly are independent of $d$, $K$ and the batch size $m$, under appropriate choices of a slightly decreased learning rate. For bounded nonconvex losses and a batch size $m=1$, we additionally show that both generalization error and learning rate are independent of $d$ and $K$, and remain essentially the same as for the SGD, even for two function evaluations. Our results extensively extend and consistently recover established results for SGD in prior work, on both generalization bounds and corresponding learning rates. If additionally $m=n$, where $n$ is the dataset size, we derive generalization guarantees for full-batch GD as well.

FedSKETCH: Communication-Efficient and Private Federated Learning via Sketching

Communication complexity and privacy are the two key challenges in Federated Learning where the goal is to perform a distributed learning through a large volume of devices. In this work, we introduce FedSKETCH and FedSKETCHGATE algorithms to address both challenges in Federated learning jointly, where these algorithms are intended to be used for homogeneous and heterogeneous data distribution settings respectively. The key idea is to compress the accumulation of local gradients using count sketch, therefore, the server does not have access to the gradients themselves which provides privacy. Furthermore, due to the lower dimension of sketching used, our method exhibits communication-efficiency property as well. We provide, for the aforementioned schemes, sharp convergence guarantees. Finally, we back up our theory with various set of experiments.

Federated Learning with Compression: Unified Analysis and Sharp Guarantees

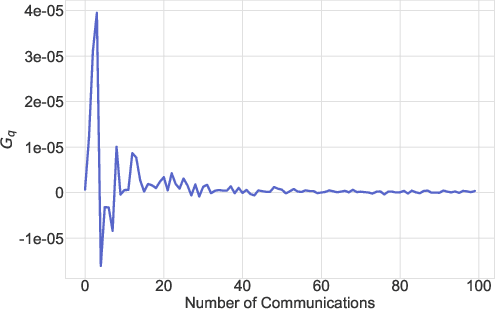
In federated learning, communication cost is often a critical bottleneck to scale up distributed optimization algorithms to collaboratively learn a model from millions of devices with potentially unreliable or limited communication and heterogeneous data distributions. Two notable trends to deal with the communication overhead of federated algorithms are \emph{gradient compression} and \emph{local computation with periodic communication}. Despite many attempts, characterizing the relationship between these two approaches has proven elusive. We address this by proposing a set of algorithms with periodical compressed (quantized or sparsified) communication and analyze their convergence properties in both homogeneous and heterogeneous local data distributions settings. For the homogeneous setting, our analysis improves existing bounds by providing tighter convergence rates for both \emph{strongly convex} and \emph{non-convex} objective functions. To mitigate data heterogeneity, we introduce a \emph{local gradient tracking} scheme and obtain sharp convergence rates that match the best-known communication complexities without compression for convex, strongly convex, and nonconvex settings. We complement our theoretical results and demonstrate the effectiveness of our proposed methods by several experiments on real-world datasets.

On the Convergence of Local Descent Methods in Federated Learning

In federated distributed learning, the goal is to optimize a global training objective defined over distributed devices, where the data shard at each device is sampled from a possibly different distribution (a.k.a., heterogeneous or non i.i.d. data samples). In this paper, we generalize the local stochastic and full gradient descent with periodic averaging-- originally designed for homogeneous distributed optimization, to solve nonconvex optimization problems in federated learning. Although scant research is available on the effectiveness of local SGD in reducing the number of communication rounds in homogeneous setting, its convergence and communication complexity in heterogeneous setting is mostly demonstrated empirically and lacks through theoretical understating. To bridge this gap, we demonstrate that by properly analyzing the effect of unbiased gradients and sampling schema in federated setting, under mild assumptions, the implicit variance reduction feature of local distributed methods generalize to heterogeneous data shards and exhibits the best known convergence rates of homogeneous setting both in general nonconvex and under {\pl}~ condition (generalization of strong-convexity). Our theoretical results complement the recent empirical studies that demonstrate the applicability of local GD/SGD to federated learning. We also specialize the proposed local method for networked distributed optimization. To the best of our knowledge, the obtained convergence rates are the sharpest known to date on the convergence of local decant methods with periodic averaging for solving nonconvex federated optimization in both centralized and networked distributed optimization.

Efficient Fair Principal Component Analysis

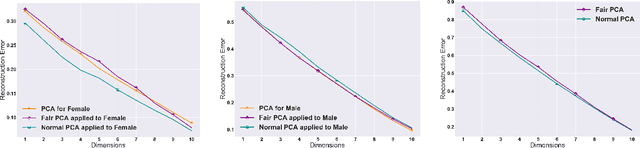
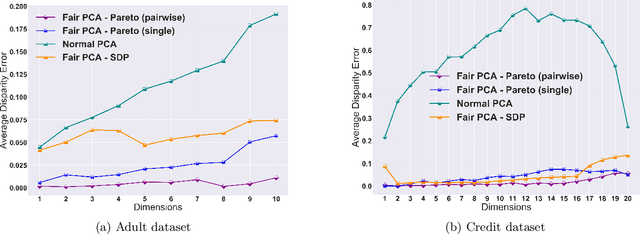
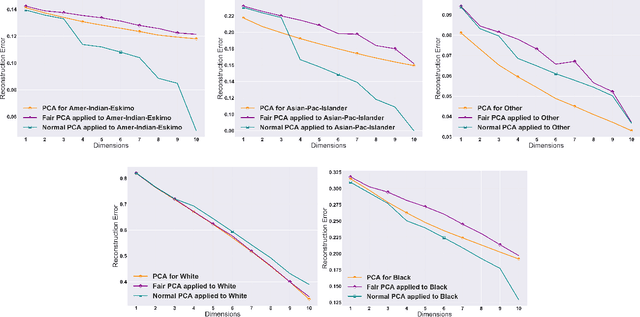
The flourishing assessments of fairness measure in machine learning algorithms have shown that dimension reduction methods such as PCA treat data from different sensitive groups unfairly. In particular, by aggregating data of different groups, the reconstruction error of the learned subspace becomes biased towards some populations that might hurt or benefit those groups inherently, leading to an unfair representation. On the other hand, alleviating the bias to protect sensitive groups in learning the optimal projection, would lead to a higher reconstruction error overall. This introduces a trade-off between sensitive groups' sacrifices and benefits, and the overall reconstruction error. In this paper, in pursuit of achieving fairness criteria in PCA, we introduce a more efficient notion of Pareto fairness, cast the Pareto fair dimensionality reduction as a multi-objective optimization problem, and propose an adaptive gradient-based algorithm to solve it. Using the notion of Pareto optimality, we can guarantee that the solution of our proposed algorithm belongs to the Pareto frontier for all groups, which achieves the optimal trade-off between those aforementioned conflicting objectives. This framework can be efficiently generalized to multiple group sensitive features, as well. We provide convergence analysis of our algorithm for both convex and non-convex objectives and show its efficacy through empirical studies on different datasets, in comparison with the state-of-the-art algorithm.

Local SGD with Periodic Averaging: Tighter Analysis and Adaptive Synchronization

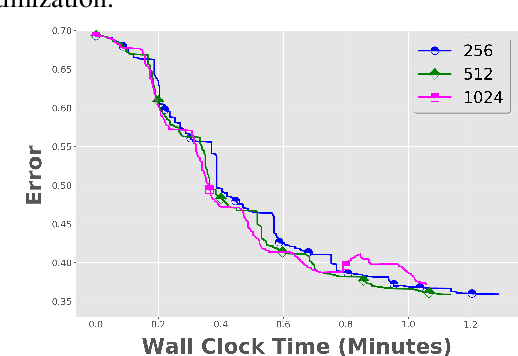
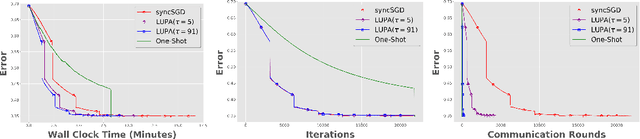
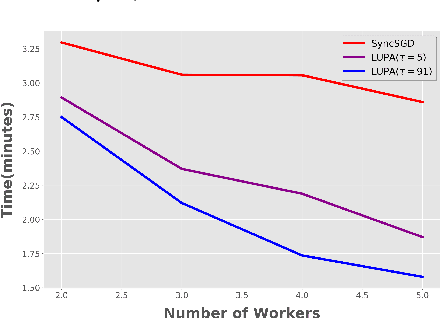
Communication overhead is one of the key challenges that hinders the scalability of distributed optimization algorithms. In this paper, we study local distributed SGD, where data is partitioned among computation nodes, and the computation nodes perform local updates with periodically exchanging the model among the workers to perform averaging. While local SGD is empirically shown to provide promising results, a theoretical understanding of its performance remains open. We strengthen convergence analysis for local SGD, and show that local SGD can be far less expensive and applied far more generally than current theory suggests. Specifically, we show that for loss functions that satisfy the Polyak-{\L}ojasiewicz condition, $O((pT)^{1/3})$ rounds of communication suffice to achieve a linear speed up, that is, an error of $O(1/pT)$, where $T$ is the total number of model updates at each worker. This is in contrast with previous work which required higher number of communication rounds, as well as was limited to strongly convex loss functions, for a similar asymptotic performance. We also develop an adaptive synchronization scheme that provides a general condition for linear speed up. Finally, we validate the theory with experimental results, running over AWS EC2 clouds and an internal GPU cluster.

Low-Complexity Stochastic Generalized Belief Propagation

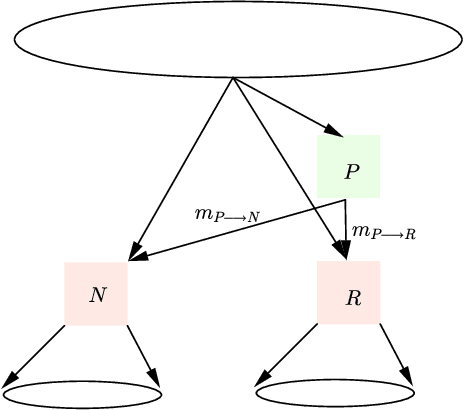
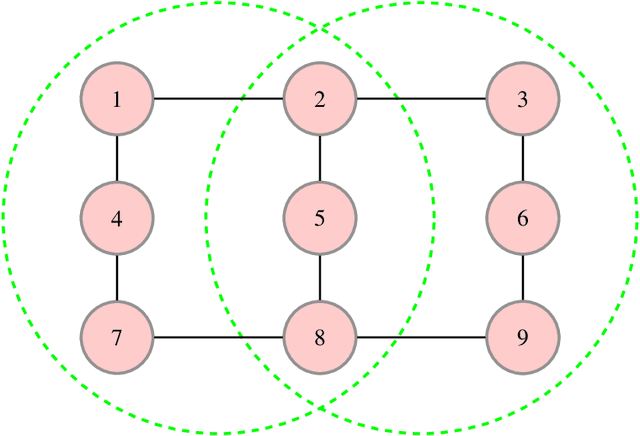
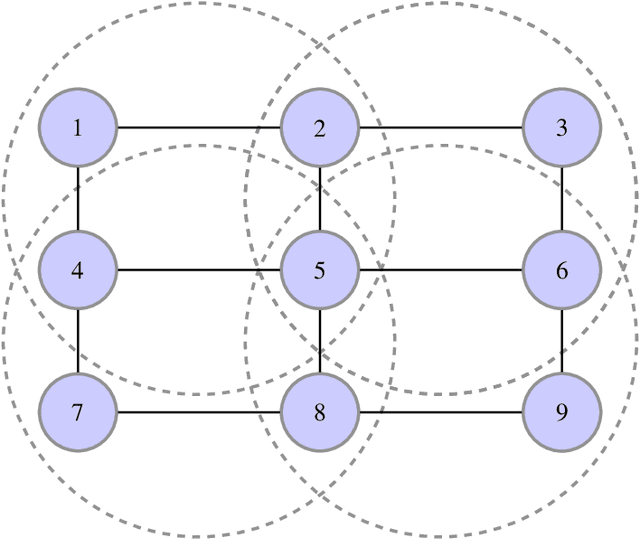
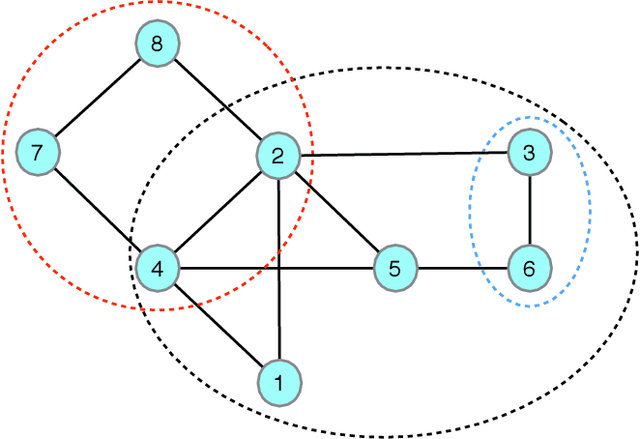
The generalized belief propagation (GBP), introduced by Yedidia et al., is an extension of the belief propagation (BP) algorithm, which is widely used in different problems involved in calculating exact or approximate marginals of probability distributions. In many problems, it has been observed that the accuracy of GBP considerably outperforms that of BP. However, because in general the computational complexity of GBP is higher than BP, its application is limited in practice. In this paper, we introduce a stochastic version of GBP called stochastic generalized belief propagation (SGBP) that can be considered as an extension to the stochastic BP (SBP) algorithm introduced by Noorshams et al. They have shown that SBP reduces the complexity per iteration of BP by an order of magnitude in alphabet size. In contrast to SBP, SGBP can reduce the computation complexity if certain topological conditions are met by the region graph associated to a graphical model. However, this reduction can be larger than only one order of magnitude in alphabet size. In this paper, we characterize these conditions and the amount of computation gain that we can obtain by using SGBP. Finally, using similar proof techniques employed by Noorshams et al., for general graphical models satisfy contraction conditions, we prove the asymptotic convergence of SGBP to the unique GBP fixed point, as well as providing non-asymptotic upper bounds on the mean square error and on the high probability error.