Game of Coding: Sybil Resistant Decentralized Machine Learning with Minimal Trust Assumption

Coding theory plays a crucial role in ensuring data integrity and reliability across various domains, from communication to computation and storage systems. However, its reliance on trust assumptions for data recovery poses significant challenges, particularly in emerging decentralized systems where trust is scarce. To address this, the game of coding framework was introduced, offering insights into strategies for data recovery within incentive-oriented environments. The focus of the earliest version of the game of coding was limited to scenarios involving only two nodes. This paper investigates the implications of increasing the number of nodes in the game of coding framework, particularly focusing on scenarios with one honest node and multiple adversarial nodes. We demonstrate that despite the increased flexibility for the adversary with an increasing number of adversarial nodes, having more power is not beneficial for the adversary and is not detrimental to the data collector, making this scheme sybil-resistant. Furthermore, we outline optimal strategies for the data collector in terms of accepting or rejecting the inputs, and characterize the optimal noise distribution for the adversary.

Correlated Privacy Mechanisms for Differentially Private Distributed Mean Estimation

Differentially private distributed mean estimation (DP-DME) is a fundamental building block in privacy-preserving federated learning, where a central server estimates the mean of $d$-dimensional vectors held by $n$ users while ensuring $(\epsilon,\delta)$-DP. Local differential privacy (LDP) and distributed DP with secure aggregation (SecAgg) are the most common notions of DP used in DP-DME settings with an untrusted server. LDP provides strong resilience to dropouts, colluding users, and malicious server attacks, but suffers from poor utility. In contrast, SecAgg-based DP-DME achieves an $O(n)$ utility gain over LDP in DME, but requires increased communication and computation overheads and complex multi-round protocols to handle dropouts and malicious attacks. In this work, we propose CorDP-DME, a novel DP-DME mechanism that spans the gap between DME with LDP and distributed DP, offering a favorable balance between utility and resilience to dropout and collusion. CorDP-DME is based on correlated Gaussian noise, ensuring DP without the perfect conditional privacy guarantees of SecAgg-based approaches. We provide an information-theoretic analysis of CorDP-DME, and derive theoretical guarantees for utility under any given privacy parameters and dropout/colluding user thresholds. Our results demonstrate that (anti) correlated Gaussian DP mechanisms can significantly improve utility in mean estimation tasks compared to LDP -- even in adversarial settings -- while maintaining better resilience to dropouts and attacks compared to distributed DP.

Differentially Private Secure Multiplication: Hiding Information in the Rubble of Noise

We consider the problem of private distributed multi-party multiplication. It is well-established that Shamir secret-sharing coding strategies can enable perfect information-theoretic privacy in distributed computation via the celebrated algorithm of Ben Or, Goldwasser and Wigderson (the "BGW algorithm"). However, perfect privacy and accuracy require an honest majority, that is, $N \geq 2t+1$ compute nodes are required to ensure privacy against any $t$ colluding adversarial nodes. By allowing for some controlled amount of information leakage and approximate multiplication instead of exact multiplication, we study coding schemes for the setting where the number of honest nodes can be a minority, that is $N< 2t+1.$ We develop a tight characterization privacy-accuracy trade-off for cases where $N < 2t+1$ by measuring information leakage using {differential} privacy instead of perfect privacy, and using the mean squared error metric for accuracy. A novel technical aspect is an intricately layered noise distribution that merges ideas from differential privacy and Shamir secret-sharing at different layers.

Local SGD with Periodic Averaging: Tighter Analysis and Adaptive Synchronization

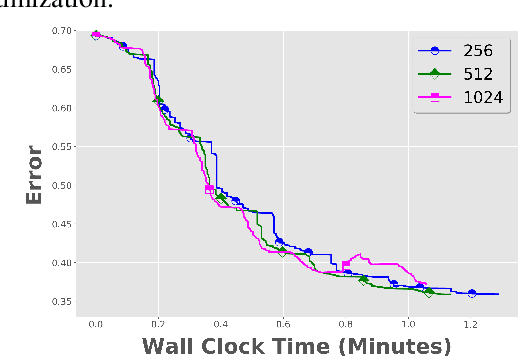
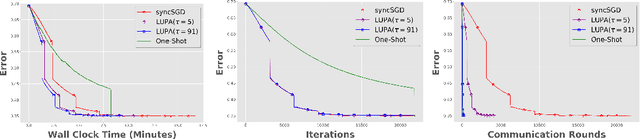
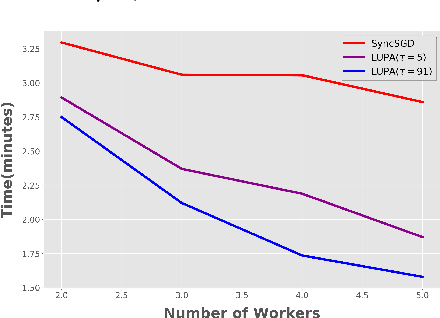
Communication overhead is one of the key challenges that hinders the scalability of distributed optimization algorithms. In this paper, we study local distributed SGD, where data is partitioned among computation nodes, and the computation nodes perform local updates with periodically exchanging the model among the workers to perform averaging. While local SGD is empirically shown to provide promising results, a theoretical understanding of its performance remains open. We strengthen convergence analysis for local SGD, and show that local SGD can be far less expensive and applied far more generally than current theory suggests. Specifically, we show that for loss functions that satisfy the Polyak-{\L}ojasiewicz condition, $O((pT)^{1/3})$ rounds of communication suffice to achieve a linear speed up, that is, an error of $O(1/pT)$, where $T$ is the total number of model updates at each worker. This is in contrast with previous work which required higher number of communication rounds, as well as was limited to strongly convex loss functions, for a similar asymptotic performance. We also develop an adaptive synchronization scheme that provides a general condition for linear speed up. Finally, we validate the theory with experimental results, running over AWS EC2 clouds and an internal GPU cluster.