Local SGD with Periodic Averaging: Tighter Analysis and Adaptive Synchronization
Paper and Code
Oct 30, 2019
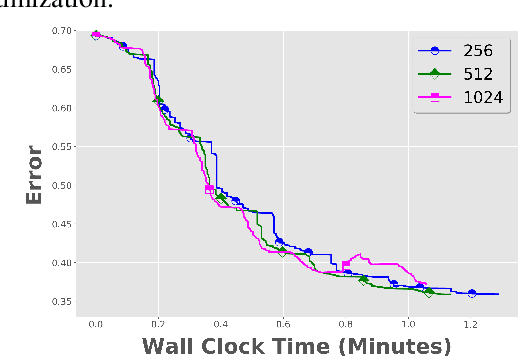
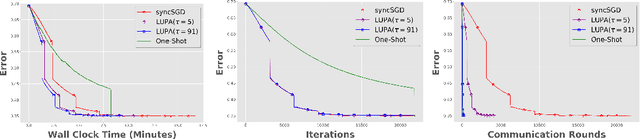
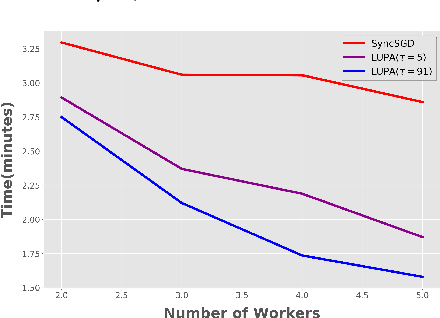
Communication overhead is one of the key challenges that hinders the scalability of distributed optimization algorithms. In this paper, we study local distributed SGD, where data is partitioned among computation nodes, and the computation nodes perform local updates with periodically exchanging the model among the workers to perform averaging. While local SGD is empirically shown to provide promising results, a theoretical understanding of its performance remains open. We strengthen convergence analysis for local SGD, and show that local SGD can be far less expensive and applied far more generally than current theory suggests. Specifically, we show that for loss functions that satisfy the Polyak-{\L}ojasiewicz condition, $O((pT)^{1/3})$ rounds of communication suffice to achieve a linear speed up, that is, an error of $O(1/pT)$, where $T$ is the total number of model updates at each worker. This is in contrast with previous work which required higher number of communication rounds, as well as was limited to strongly convex loss functions, for a similar asymptotic performance. We also develop an adaptive synchronization scheme that provides a general condition for linear speed up. Finally, we validate the theory with experimental results, running over AWS EC2 clouds and an internal GPU cluster.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge