Distributed Personalized Empirical Risk Minimization

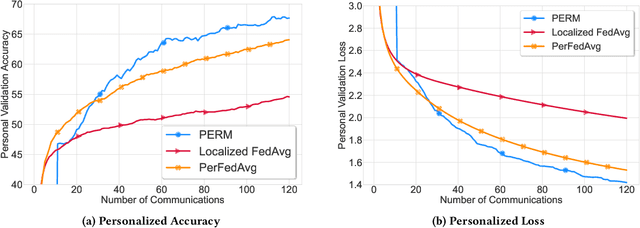
This paper advocates a new paradigm Personalized Empirical Risk Minimization (PERM) to facilitate learning from heterogeneous data sources without imposing stringent constraints on computational resources shared by participating devices. In PERM, we aim to learn a distinct model for each client by learning who to learn with and personalizing the aggregation of local empirical losses by effectively estimating the statistical discrepancy among data distributions, which entails optimal statistical accuracy for all local distributions and overcomes the data heterogeneity issue. To learn personalized models at scale, we propose a distributed algorithm that replaces the standard model averaging with model shuffling to simultaneously optimize PERM objectives for all devices. This also allows us to learn distinct model architectures (e.g., neural networks with different numbers of parameters) for different clients, thus confining underlying memory and compute resources of individual clients. We rigorously analyze the convergence of the proposed algorithm and conduct experiments that corroborate the effectiveness of the proposed paradigm.

FedRule: Federated Rule Recommendation System with Graph Neural Networks

Much of the value that IoT (Internet-of-Things) devices bring to ``smart'' homes lies in their ability to automatically trigger other devices' actions: for example, a smart camera triggering a smart lock to unlock a door. Manually setting up these rules for smart devices or applications, however, is time-consuming and inefficient. Rule recommendation systems can automatically suggest rules for users by learning which rules are popular based on those previously deployed (e.g., in others' smart homes). Conventional recommendation formulations require a central server to record the rules used in many users' homes, which compromises their privacy and leaves them vulnerable to attacks on the central server's database of rules. Moreover, these solutions typically leverage generic user-item matrix methods that do not fully exploit the structure of the rule recommendation problem. In this paper, we propose a new rule recommendation system, dubbed as FedRule, to address these challenges. One graph is constructed per user upon the rules s/he is using, and the rule recommendation is formulated as a link prediction task in these graphs. This formulation enables us to design a federated training algorithm that is able to keep users' data private. Extensive experiments corroborate our claims by demonstrating that FedRule has comparable performance as the centralized setting and outperforms conventional solutions.

Learning Distributionally Robust Models at Scale via Composite Optimization

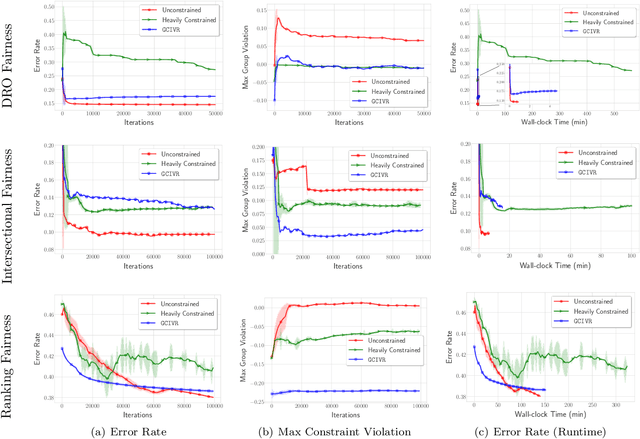
To train machine learning models that are robust to distribution shifts in the data, distributionally robust optimization (DRO) has been proven very effective. However, the existing approaches to learning a distributionally robust model either require solving complex optimization problems such as semidefinite programming or a first-order method whose convergence scales linearly with the number of data samples -- which hinders their scalability to large datasets. In this paper, we show how different variants of DRO are simply instances of a finite-sum composite optimization for which we provide scalable methods. We also provide empirical results that demonstrate the effectiveness of our proposed algorithm with respect to the prior art in order to learn robust models from very large datasets.

Adaptive Distillation: Aggregating Knowledge from Multiple Paths for Efficient Distillation

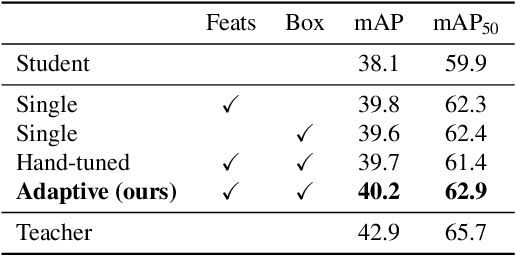
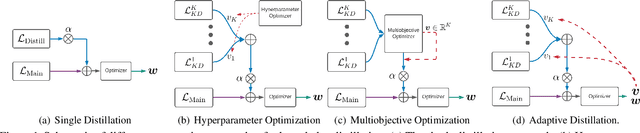
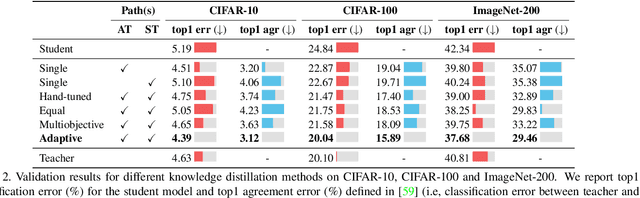
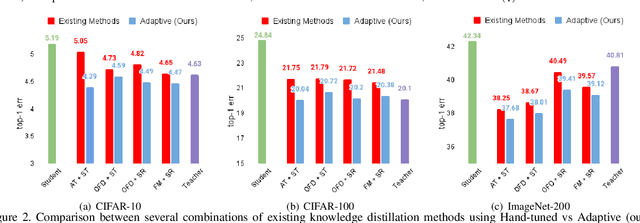
Knowledge Distillation is becoming one of the primary trends among neural network compression algorithms to improve the generalization performance of a smaller student model with guidance from a larger teacher model. This momentous rise in applications of knowledge distillation is accompanied by the introduction of numerous algorithms for distilling the knowledge such as soft targets and hint layers. Despite this advancement in different techniques for distilling the knowledge, the aggregation of different paths for distillation has not been studied comprehensively. This is of particular significance, not only because different paths have different importance, but also due to the fact that some paths might have negative effects on the generalization performance of the student model. Hence, we need to adaptively adjust the importance of each path to maximize the impact of distillation on the student model. In this paper, we explore different approaches for aggregating these different paths and introduce our proposed adaptive approach based on multitask learning methods. We empirically demonstrate the effectiveness of the proposed approach over other baselines on the applications of knowledge distillation in classification, semantic segmentation, and object detection tasks.

Pareto Efficient Fairness in Supervised Learning: From Extraction to Tracing

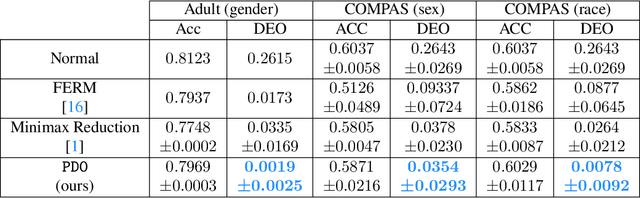
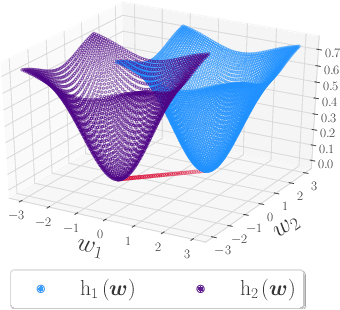
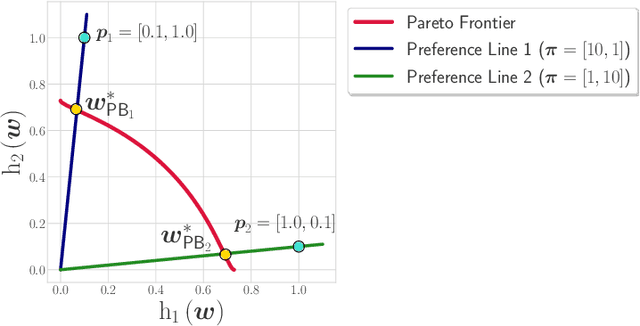
As algorithmic decision-making systems are becoming more pervasive, it is crucial to ensure such systems do not become mechanisms of unfair discrimination on the basis of gender, race, ethnicity, religion, etc. Moreover, due to the inherent trade-off between fairness measures and accuracy, it is desirable to learn fairness-enhanced models without significantly compromising the accuracy. In this paper, we propose Pareto efficient Fairness (PEF) as a suitable fairness notion for supervised learning, that can ensure the optimal trade-off between overall loss and other fairness criteria. The proposed PEF notion is definition-agnostic, meaning that any well-defined notion of fairness can be reduced to the PEF notion. To efficiently find a PEF classifier, we cast the fairness-enhanced classification as a bilevel optimization problem and propose a gradient-based method that can guarantee the solution belongs to the Pareto frontier with provable guarantees for convex and non-convex objectives. We also generalize the proposed algorithmic solution to extract and trace arbitrary solutions from the Pareto frontier for a given preference over accuracy and fairness measures. This approach is generic and can be generalized to any multicriteria optimization problem to trace points on the Pareto frontier curve, which is interesting by its own right. We empirically demonstrate the effectiveness of the PEF solution and the extracted Pareto frontier on real-world datasets compared to state-of-the-art methods.

Distributionally Robust Federated Averaging

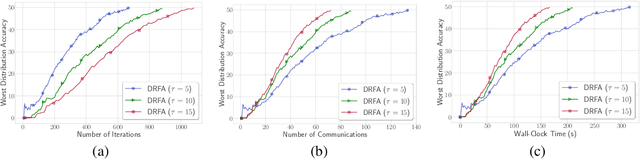
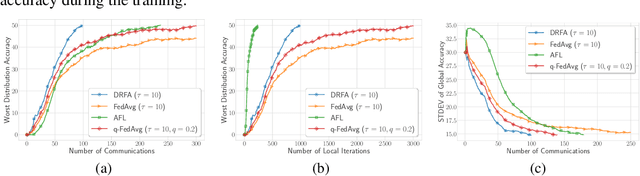
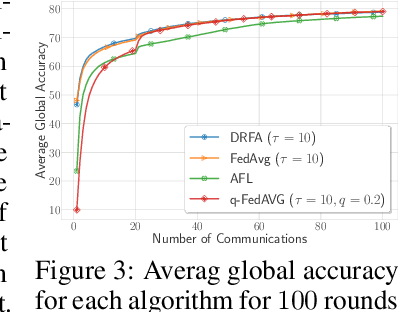
In this paper, we study communication efficient distributed algorithms for distributionally robust federated learning via periodic averaging with adaptive sampling. In contrast to standard empirical risk minimization, due to the minimax structure of the underlying optimization problem, a key difficulty arises from the fact that the global parameter that controls the mixture of local losses can only be updated infrequently on the global stage. To compensate for this, we propose a Distributionally Robust Federated Averaging (DRFA) algorithm that employs a novel snapshotting scheme to approximate the accumulation of history gradients of the mixing parameter. We analyze the convergence rate of DRFA in both convex-linear and nonconvex-linear settings. We also generalize the proposed idea to objectives with regularization on the mixture parameter and propose a proximal variant, dubbed as DRFA-Prox, with provable convergence rates. We also analyze an alternative optimization method for regularized cases in strongly-convex-strongly-concave and non-convex (under PL condition)-strongly-concave settings. To the best of our knowledge, this paper is the first to solve distributionally robust federated learning with reduced communication, and to analyze the efficiency of local descent methods on distributed minimax problems. We give corroborating experimental evidence for our theoretical results in federated learning settings.

Federated Learning with Compression: Unified Analysis and Sharp Guarantees

In federated learning, communication cost is often a critical bottleneck to scale up distributed optimization algorithms to collaboratively learn a model from millions of devices with potentially unreliable or limited communication and heterogeneous data distributions. Two notable trends to deal with the communication overhead of federated algorithms are \emph{gradient compression} and \emph{local computation with periodic communication}. Despite many attempts, characterizing the relationship between these two approaches has proven elusive. We address this by proposing a set of algorithms with periodical compressed (quantized or sparsified) communication and analyze their convergence properties in both homogeneous and heterogeneous local data distributions settings. For the homogeneous setting, our analysis improves existing bounds by providing tighter convergence rates for both \emph{strongly convex} and \emph{non-convex} objective functions. To mitigate data heterogeneity, we introduce a \emph{local gradient tracking} scheme and obtain sharp convergence rates that match the best-known communication complexities without compression for convex, strongly convex, and nonconvex settings. We complement our theoretical results and demonstrate the effectiveness of our proposed methods by several experiments on real-world datasets.

Adaptive Personalized Federated Learning

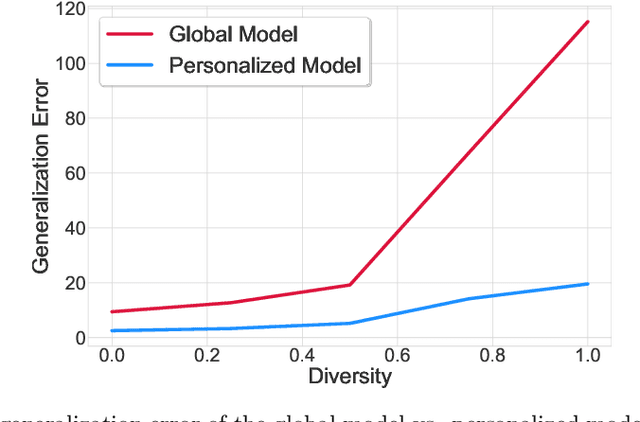
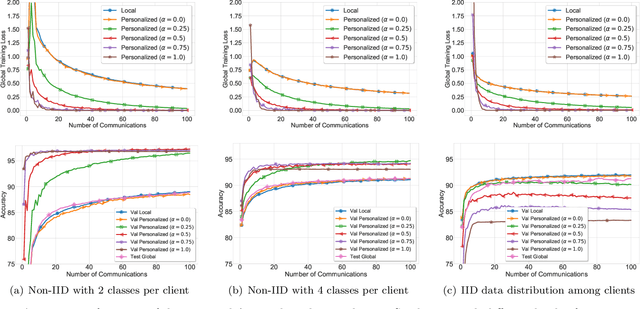
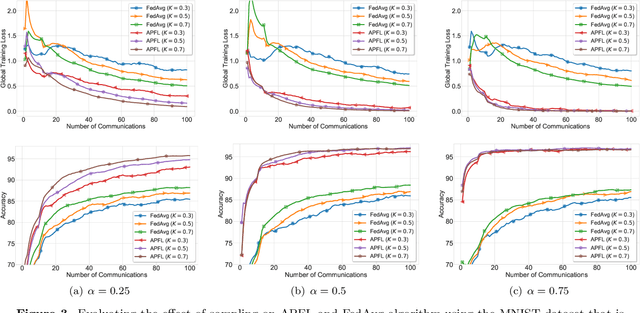
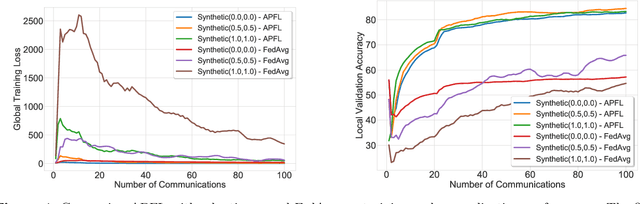
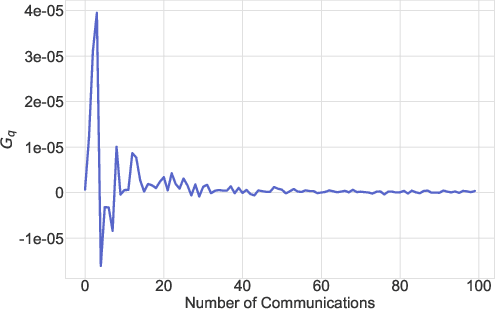
Investigation of the degree of personalization in federated learning algorithms has shown that only maximizing the performance of the global model will confine the capacity of the local models to personalize. In this paper, we advocate an adaptive personalized federated learning (APFL) algorithm, where each client will train their local models while contributing to the global model. Theoretically, we show that the mixture of local and global models can reduce the generalization error, using the multi-domain learning theory. We also propose a communication-reduced bilevel optimization method, which reduces the communication rounds to $O(\sqrt{T})$ and show that under strong convexity and smoothness assumptions, the proposed algorithm can achieve a convergence rate of $O(1/T)$ with some residual error. The residual error is related to the gradient diversity among local models, and the gap between optimal local and global models.

Efficient Fair Principal Component Analysis

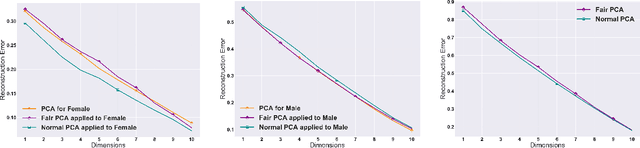
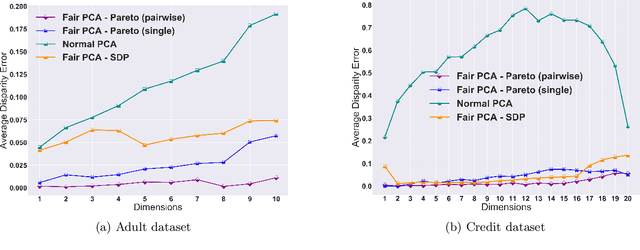
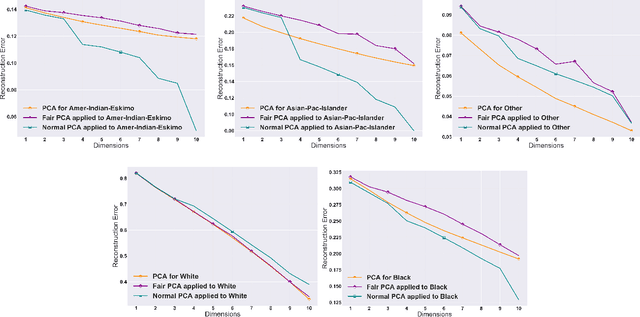
The flourishing assessments of fairness measure in machine learning algorithms have shown that dimension reduction methods such as PCA treat data from different sensitive groups unfairly. In particular, by aggregating data of different groups, the reconstruction error of the learned subspace becomes biased towards some populations that might hurt or benefit those groups inherently, leading to an unfair representation. On the other hand, alleviating the bias to protect sensitive groups in learning the optimal projection, would lead to a higher reconstruction error overall. This introduces a trade-off between sensitive groups' sacrifices and benefits, and the overall reconstruction error. In this paper, in pursuit of achieving fairness criteria in PCA, we introduce a more efficient notion of Pareto fairness, cast the Pareto fair dimensionality reduction as a multi-objective optimization problem, and propose an adaptive gradient-based algorithm to solve it. Using the notion of Pareto optimality, we can guarantee that the solution of our proposed algorithm belongs to the Pareto frontier for all groups, which achieves the optimal trade-off between those aforementioned conflicting objectives. This framework can be efficiently generalized to multiple group sensitive features, as well. We provide convergence analysis of our algorithm for both convex and non-convex objectives and show its efficacy through empirical studies on different datasets, in comparison with the state-of-the-art algorithm.