Adaptive Personalized Federated Learning

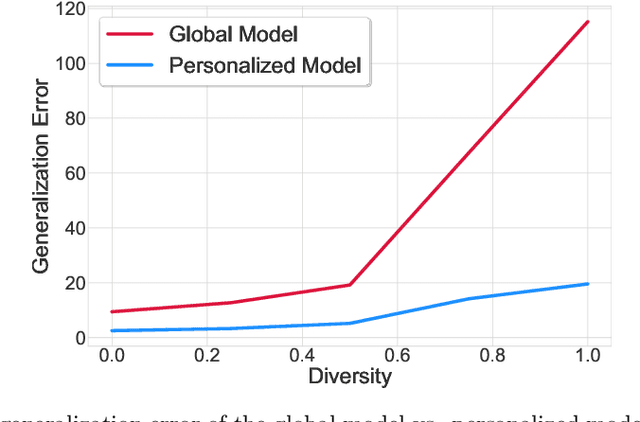
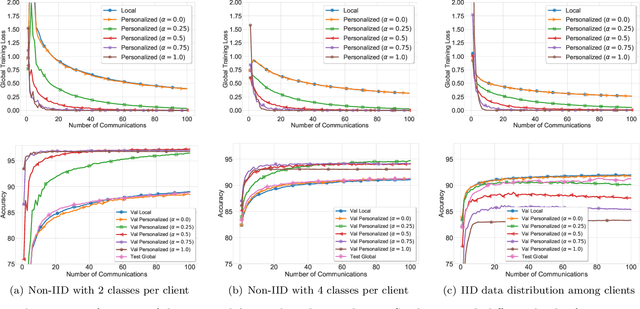
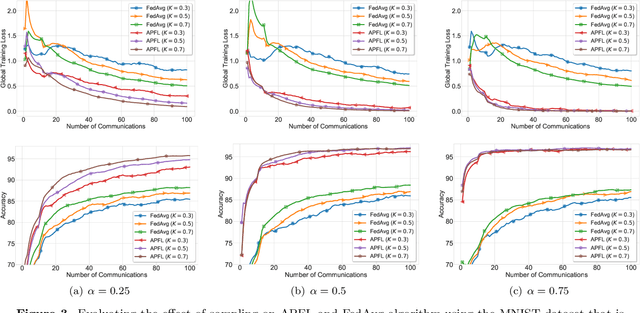
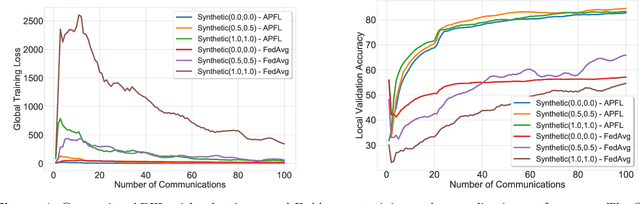
Investigation of the degree of personalization in federated learning algorithms has shown that only maximizing the performance of the global model will confine the capacity of the local models to personalize. In this paper, we advocate an adaptive personalized federated learning (APFL) algorithm, where each client will train their local models while contributing to the global model. Theoretically, we show that the mixture of local and global models can reduce the generalization error, using the multi-domain learning theory. We also propose a communication-reduced bilevel optimization method, which reduces the communication rounds to $O(\sqrt{T})$ and show that under strong convexity and smoothness assumptions, the proposed algorithm can achieve a convergence rate of $O(1/T)$ with some residual error. The residual error is related to the gradient diversity among local models, and the gap between optimal local and global models.