FEDSTR: Money-In AI-Out

The NOSTR is a communication protocol for the social web, based on the w3c websockets standard. Although it is still in its infancy, it is well known as a social media protocol, thousands of trusted users and multiple user interfaces, offering a unique experience and enormous capabilities. To name a few, the NOSTR applications include but are not limited to direct messaging, file sharing, audio/video streaming, collaborative writing, blogging and data processing through distributed AI directories. In this work, we propose an approach that builds upon the existing protocol structure with end goal a decentralized marketplace for federated learning and LLM training. In this proposed design there are two parties: on one side there are customers who provide a dataset that they want to use for training an AI model. On the other side, there are service providers, who receive (parts of) the dataset, train the AI model, and for a payment as an exchange, they return the optimized AI model. The decentralized and censorship resistant features of the NOSTR enable the possibility of designing a fair and open marketplace for training AI models and LLMs.

Federated Learning Under Restricted User Availability

Federated Learning (FL) is a decentralized machine learning framework that enables collaborative model training while respecting data privacy. In various applications, non-uniform availability or participation of users is unavoidable due to an adverse or stochastic environment, the latter often being uncontrollable during learning. Here, we posit a generic user selection mechanism implementing a possibly randomized, stationary selection policy, suggestively termed as a Random Access Model (RAM). We propose a new formulation of the FL problem which effectively captures and mitigates limited participation of data originating from infrequent, or restricted users, at the presence of a RAM. By employing the Conditional Value-at-Risk (CVaR) over the (unknown) RAM distribution, we extend the expected loss FL objective to a risk-aware objective, enabling the design of an efficient training algorithm that is completely oblivious to the RAM, and with essentially identical complexity as FedAvg. Our experiments on synthetic and benchmark datasets show that the proposed approach achieves significantly improved performance as compared with standard FL, under a variety of setups.

Repeated Random Sampling for Minimizing the Time-to-Accuracy of Learning

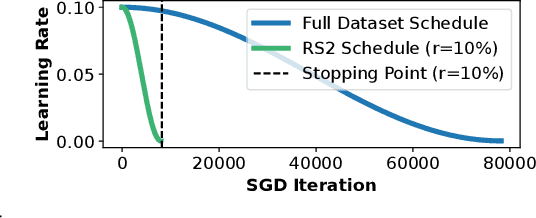
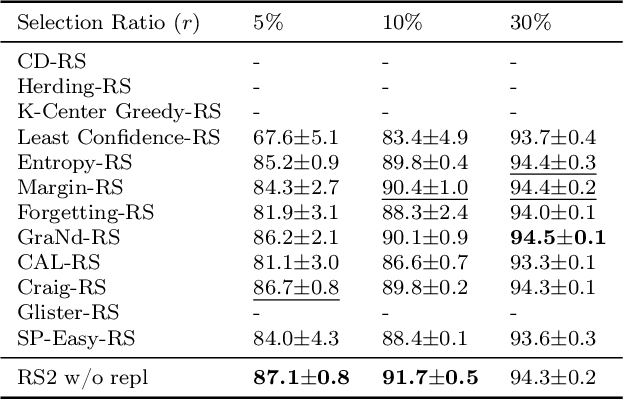
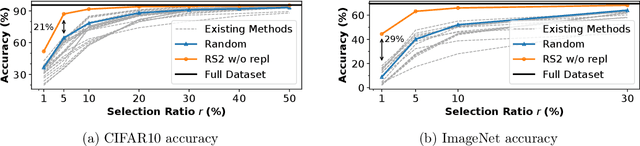
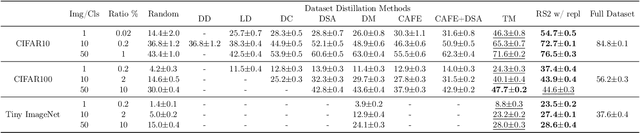
Methods for carefully selecting or generating a small set of training data to learn from, i.e., data pruning, coreset selection, and data distillation, have been shown to be effective in reducing the ever-increasing cost of training neural networks. Behind this success are rigorously designed strategies for identifying informative training examples out of large datasets. However, these strategies come with additional computational costs associated with subset selection or data distillation before training begins, and furthermore, many are shown to even under-perform random sampling in high data compression regimes. As such, many data pruning, coreset selection, or distillation methods may not reduce 'time-to-accuracy', which has become a critical efficiency measure of training deep neural networks over large datasets. In this work, we revisit a powerful yet overlooked random sampling strategy to address these challenges and introduce an approach called Repeated Sampling of Random Subsets (RSRS or RS2), where we randomly sample the subset of training data for each epoch of model training. We test RS2 against thirty state-of-the-art data pruning and data distillation methods across four datasets including ImageNet. Our results demonstrate that RS2 significantly reduces time-to-accuracy compared to existing techniques. For example, when training on ImageNet in the high-compression regime (using less than 10% of the dataset each epoch), RS2 yields accuracy improvements up to 29% compared to competing pruning methods while offering a runtime reduction of 7x. Beyond the above meta-study, we provide a convergence analysis for RS2 and discuss its generalization capability. The primary goal of our work is to establish RS2 as a competitive baseline for future data selection or distillation techniques aimed at efficient training.

Select without Fear: Almost All Mini-Batch Schedules Generalize Optimally

We establish matching upper and lower generalization error bounds for mini-batch Gradient Descent (GD) training with either deterministic or stochastic, data-independent, but otherwise arbitrary batch selection rules. We consider smooth Lipschitz-convex/nonconvex/strongly-convex loss functions, and show that classical upper bounds for Stochastic GD (SGD) also hold verbatim for such arbitrary nonadaptive batch schedules, including all deterministic ones. Further, for convex and strongly-convex losses we prove matching lower bounds directly on the generalization error uniform over the aforementioned class of batch schedules, showing that all such batch schedules generalize optimally. Lastly, for smooth (non-Lipschitz) nonconvex losses, we show that full-batch (deterministic) GD is essentially optimal, among all possible batch schedules within the considered class, including all stochastic ones.

Beyond Lipschitz: Sharp Generalization and Excess Risk Bounds for Full-Batch GD

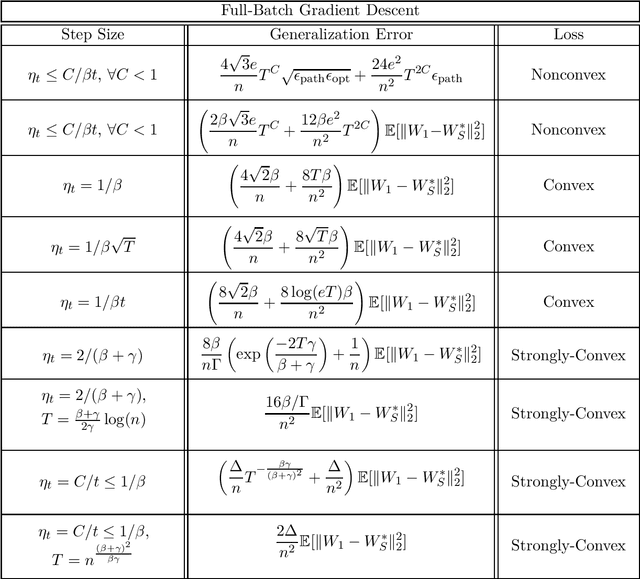
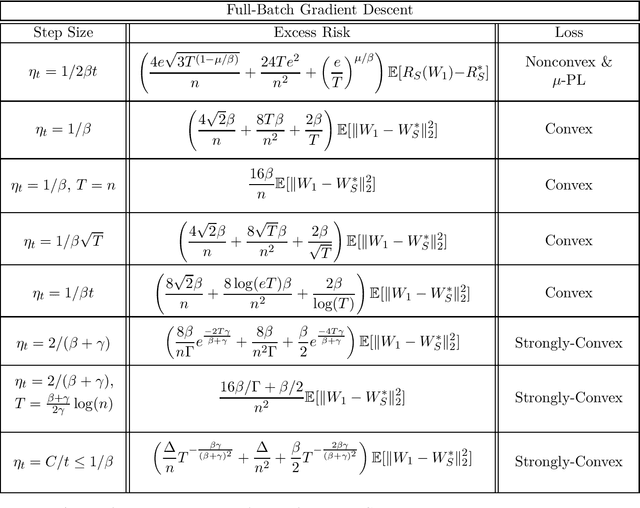
We provide sharp path-dependent generalization and excess error guarantees for the full-batch Gradient Decent (GD) algorithm for smooth losses (possibly non-Lipschitz, possibly nonconvex). At the heart of our analysis is a novel generalization error technique for deterministic symmetric algorithms, that implies average output stability and a bounded expected gradient of the loss at termination leads to generalization. This key result shows that small generalization error occurs at stationary points, and allows us to bypass Lipschitz assumptions on the loss prevalent in previous work. For nonconvex, convex and strongly convex losses, we show the explicit dependence of the generalization error in terms of the accumulated path-dependent optimization error, terminal optimization error, number of samples, and number of iterations. For nonconvex smooth losses, we prove that full-batch GD efficiently generalizes close to any stationary point at termination, under the proper choice of a decreasing step size. Further, if the loss is nonconvex but the objective is PL, we derive vanishing bounds on the corresponding excess risk. For convex and strongly-convex smooth losses, we prove that full-batch GD generalizes even for large constant step sizes, and achieves a small excess risk while training fast. Our full-batch GD generalization error and excess risk bounds are significantly tighter than the existing bounds for (stochastic) GD, when the loss is smooth (but possibly non-Lipschitz).

Black-Box Generalization

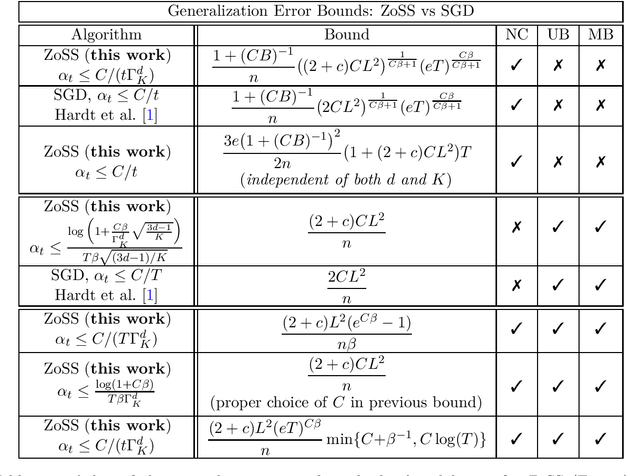
We provide the first generalization error analysis for black-box learning through derivative-free optimization. Under the assumption of a Lipschitz and smooth unknown loss, we consider the Zeroth-order Stochastic Search (ZoSS) algorithm, that updates a $d$-dimensional model by replacing stochastic gradient directions with stochastic differences of $K+1$ perturbed loss evaluations per dataset (example) query. For both unbounded and bounded possibly nonconvex losses, we present the first generalization bounds for the ZoSS algorithm. These bounds coincide with those for SGD, and rather surprisingly are independent of $d$, $K$ and the batch size $m$, under appropriate choices of a slightly decreased learning rate. For bounded nonconvex losses and a batch size $m=1$, we additionally show that both generalization error and learning rate are independent of $d$ and $K$, and remain essentially the same as for the SGD, even for two function evaluations. Our results extensively extend and consistently recover established results for SGD in prior work, on both generalization bounds and corresponding learning rates. If additionally $m=n$, where $n$ is the dataset size, we derive generalization guarantees for full-batch GD as well.

Non-Parametric Structure Learning on Hidden Tree-Shaped Distributions

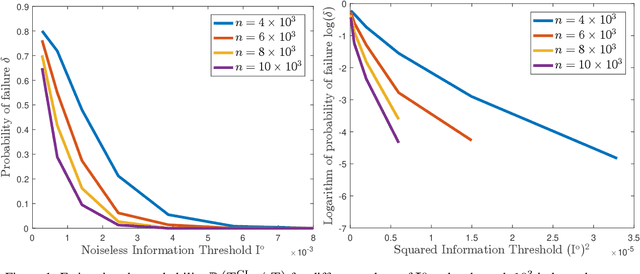
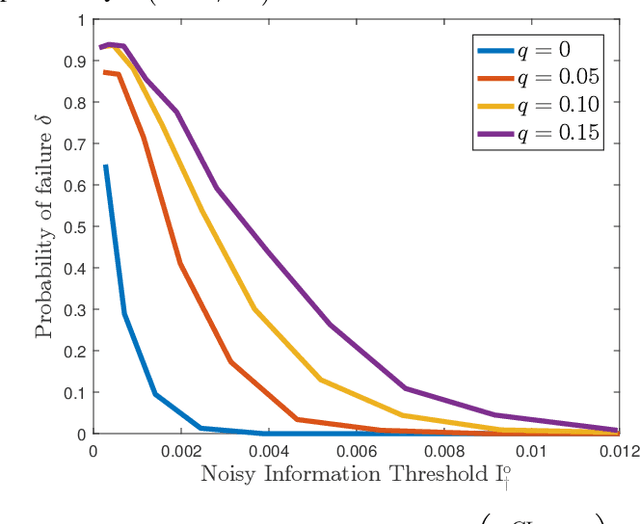
We provide high probability sample complexity guarantees for non-parametric structure learning of tree-shaped graphical models whose nodes are discrete random variables with a finite or countable alphabet, both in the noiseless and noisy regimes. First, we introduce a new, fundamental quantity called the (noisy) information threshold, which arises naturally from the error analysis of the Chow-Liu algorithm and characterizes not only the sample complexity, but also the inherent impact of the noise on the structure learning task, without explicit assumptions on the distribution of the model. This allows us to present the first non-parametric, high-probability finite sample complexity bounds on tree-structure learning from potentially noise-corrupted data. In particular, for number of nodes $p$, success rate $1-\delta$, and a fixed value of the information threshold, our sample complexity bounds for exact structure recovery are of the order of $\mathcal{O}\big(\log^{1+\zeta} (p/\delta)\big) $, for all $\zeta>0$, for both noiseless and noisy settings. Subsequently, we apply our results on two classes of hidden models, namely, the $M$-ary erasure channel and the generalized symmetric channel, illustrating the usefulness and importance of our framework. As a byproduct of our analysis, this paper resolves the open problem of tree structure learning in the presence of non-identically distributed observation noise, providing explicit conditions on the convergence of the Chow-Liu algorithm under this setting as well.

Predictive Learning on Sign-Valued Hidden Markov Trees

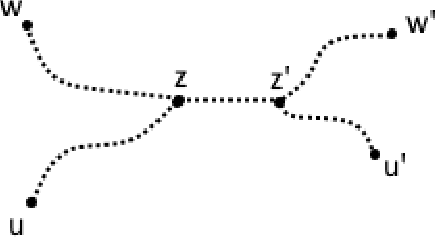
We provide high-probability sample complexity guarantees for exact structure recovery and accurate Predictive Learning using noise-corrupted samples from an acyclic (tree-shaped) graphical model. The hidden variables follow a tree-structured Ising model distribution whereas the observable variables are generated by a binary symmetric channel, taking the hidden variables as its input. This model arises naturally in a variety of applications, such as in physics, biology, computer science, and finance. The noiseless structure learning problem has been studied earlier by Bresler and Karzand (2018); this paper quantifies how noise in the hidden model impacts the sample complexity of structure learning and predictive distributional inference by proving upper and lower bounds on the sample complexity. Quite remarkably, for any tree with $p$ vertices and probability of incorrect recovery $\delta>0$, the order of necessary number of samples remains logarithmic as in the noiseless case, i.e., $\mathcal{O}(\log(p/\delta))$, for both aforementioned tasks. We also present a new equivalent of Isserlis' Theorem for sign-valued tree-structured distributions, yielding a new low-complexity algorithm for higher order moment estimation.